Математика 6 класс учебник Виленкин, Жохов 1 часть ответы – проверочная работа на 78 странице

- Тип: ГДЗ, Решебник.
- Авторы: Виленкин Н.Я., Жихов В.И., Чесноков А.С. и др.
- Часть: 1.
- Год: 2023-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Проверьте себя
Проверочная работа №1
Номер 1.
Восстановите алгоритм сложения смешанных чисел, записав в нужном порядке номера действий: а) при необходимости сократить дробь, выделить целую часть и прибавить её к полученной целой части; б) привести к наименьшему общему знаменателю дробные части чисел; в) отдельно выполнить сложение целых и отдельно дробных частей.
Ответ:2); 3); 1)
Номер 2.
Запишите выражение и найдите его значение: а) к сумме чисел 11/3 и 51/9 прибавить 45/24; б) к 12/65 прибавить сумму чисел 61/10 и 33/25.
Ответ:
а) (11/3 + 51/9) + 45/24 = 1047/72
1) 11⁽³/3 + 51⁽¹/9 = 13/9 + 51/9 = 64/9
2) 64⁽⁸/9 + 45⁽³/24 = 632/72 + 415/72 = 1047/72
б) 12/65 + (61/10 + 33/25) = 10163/650
1) 61⁽⁵/10 + 33⁽²/25 = 65/50 + 36/50 = 911/50
2) 12⁽¹⁰/65 + 911⁽¹³/50 = 120/650 + 9143/650 = 10163/650.
Номер 3.
Найдите периметр треугольника ABC, если AB = 51/12 см, BC = 61/5 см и AC = 41/6 см.
Ответ:P = AB + BC + AC 51⁽⁵/12 + 61⁽¹²/5 + 41⁽¹⁰/6 = 55/60 + 612/60 + 410/60 = 1527 : 3/60 : 3 = 159/20 (см) Ответ: 159/20 см периметр треугольника АВС.
Проверочная работа №2
Номер 1.
Запишите выражение и найдите его значение: а) к разности чисел 62/3 и 21/6 прибавить 35/12; б) из суммы чисел 12/15 и 57/30 вычесть 51/30.
Ответ:
а) (62/3 − 21/6) + 35/12 = 711/12
1) 62⁽²/3 − 21⁽²/6 = 64/6 − 21/6 = 43/6 = 41/2
2) 41⁽⁶/2 + 35/12 = 46/12 + 35/12 = 711/12
б) (12/15 + 57/30) − 51/30 = 611/30 − 51/30 = 11/3
1) 12⁽²/15 + 57/30 = 14/30 + 57/30 = 611/30
2) 611/30 − 51/30 = 110 : 10/30 : 10 = 11/3
Номер 2.
Решите уравнение и сделайте проверку: а) x + 34/7 = 62/21; б) 57/12 + x = 85/16
Ответ:
а) х + 34/7 = 62/21
x = 62⁽¹/21 − 34⁽³/7
x = 62/21 − 312/21
x = 523/21 − 312/21
x = 211/21
Проверка: 211/21 + 34⁽³/7 = 62/21
211/21 + 312/21 = 62/21
523/21 = 62/21
62/21 = 62/21
б) 57/12 + x = 85/16
х = 85⁽³/16 − 57⁽⁴/12
х = 815/48 − 528/48
х = 763/48 − 528/48
x = 235/48
Проверка: 57⁽⁴/12 + 235/48 = 85/16
528/48 + 235/48 = 85/16
763/48 = 85/16
815 : 3/48 : 3 = 85/16
85/16 = 85/16
Номер 3.
С поля площадью 25 га собрали 1052 ц пшеницы, а с поля площадью 30 га собрали 1463 ц пшеницы. а) Найдите урожайность пшеницы на каждом поле. б) На каком поле урожайность пшеницы выше? На сколько?
Ответ:а) 1) 1052 : 25 = 1052/25 = 422/25 (ц/га) − урожайность 1 поля; 2) 1463 : 30 = 1463/30 = 4823/30 (ц/га) − урожайность 2 поля; Ответ: урожайность пшеницы с первого поля − 422/25 ц/га и со второго поля − 4823/30 ц/га. б) 4823⁽⁵/30 − 422⁽⁶/25 = 48115/150 − 4212/150 = 6103/150 (ц/га) Ответ: со второго поля урожайность больше на 6103/150 ц/га.
Номер 4*.
На сколько сумма чисел 4439/751 и 24/7 больше разности этих чисел?
Ответ:(4439/751 + 24/7) − (4439/751 − 24/7)= 4439/751 + 24/7 − 4439/751+ 24/7 = 48/7 = 51/7 Ответ: сумма больше разности на 51/7.
Проверочная работа №3
Номер 1.
Найдите значение числового выражения наиболее удобным способом: а) 24/15 + 171/80 + 311/15; б) 37/16 − (13/8 + 13/16).
Ответ:а) 24/15 + 171/80 + 311/15 = 6311/240 = (24/15 + 311/15) + 171/80 = 515/15 + 171/80 = 6 + 171/80 = 771/80. б) 37/16 − (13/8 + 13/16) = (37/16 − 13/16) − 13/8 = 24 : 2/16 : 2 − 13/8 = 22/8 − 13/8 = 110/8 − 13/8 = 7/8.
Номер 2.
Представьте десятичную дробь в виде смешанного числа и вычислите:
а) 23/15 − 1,9 + 17/20;
б) 2,34 + 41/6 − 214/15
а) 23/15 − 1,9 + 17/20 = 23⁽⁴/15 − 19⁽⁶/10 + 17⁽³/20 = 212/60 − 154/60 + 121/60 =
172/60 − 154/60 + 121/60 = 139 : 3/60 : 3 = 113/20
б) 2,34 + 41/6 − 214/15 = 234 : 2/100 : 2 + 41/6 − 214/15 = 217⁽³/50 + 41⁽²⁵/6 − 214⁽¹⁰/15 =
251/150 + 425/150 − 2140/150 =
676/150 − 2140/150 =
5226/150 − 2140/150 = 386 : 2/150 : 2 = 343/75.
Номер 3.
Запишите равенство, обозначив неизвестное через x, и найдите x: а) число прибавили к 1/2 и получили 13/14; б) число уменьшили на 18/9 и получили 62/3; в) к числу прибавили 103/14 и получили 1211/42; г) из числа вычли 45/36 и получили 34/39
Ответ:
а) х + 1/2 = 13/14
x = 13⁽¹/14 − 1⁽⁷/2
x = 13/14 − 7/14
x = 6 : 2/14 : 2
x = 3/7
Ответ: x = 3/7.
б) х − 18/9 = 62/3
x = 62⁽³/3 + 18⁽¹/9
x = 66/9 + 18/9
x = 714/9 = 85/9
Ответ: 85/9.
в) х + 103/14 = 1211/42
x = 1211⁽¹/42 − 103⁽³/14
x = 1211/42 − 109/42
x = 22 : 2/42 : 2 = 21/21.
Ответ: 21/21.
г) х − 45/36 = 34/39
x = 34⁽¹²/39 + 45⁽¹³/36
x = 348/468 + 465/468
x = 7113/468
Ответ: 7113/468.
Номер 4.
Моторная лодка в стоячей воде за 9 мин преодолевает расстояние в 3750 м. Найдите скорость моторной лодки по течению и скорость против течения, если скорость течения реки равна 205/6 м/мин.
Ответ:1) 3750 : 9 = 3750/9 = 4166 : 3/9 : 3 = 4162/3 (м/мин) − скорость лодки в стоячей воде.
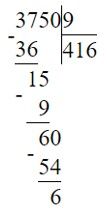
2) 4162⁽²/3 + 205/6 = 4164/6 + 205/6 = 4369 : 3/6 : 3 = 4371/2 (м/мин) − по течению; 3) 4162⁽²/3 − 205/6 = 4164/6 − 205/6 = 3955/6 (м/мин) − против течения; Ответ: 4371/2 м/мин скорость моторной лодки по течению и 3955/6 м/мин против течения.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.