Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 8

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 27.
Составь по таблице три задачи и реши их.

Задача 1:
Автобус ехал до турбазы 2 часа со скоростью 60 км/ч. Какое расстояние он прошел за это время?
60 ∙ 2 = 120 (км) – проехал автобус за 2 часа.
Ответ: 120 км всего проехал автобус за 2 часа.
Задача 2:
Поезд вёз ценный груз до города целых 120 км со скоростью 60 км/ч. Сколько времени понадобилось поезду, чтобы добраться туда?>
120 : 60 = 2 (ч) – ехал поезд.
Ответ: 2 часа всего ехал поезд.
Задача 3:
Легковая машина торопилась на автостоянку, расстояние до которой 120 км. С какой скоростью ехала машина, если она была в пути 2часа?
120 : 2 = 60 (км/ч) – скорость легкового автомобиля.
Ответ: скорость легкового автомобиля составляет 60 км/ч.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Рассмотрим таблицу, составим по ней задачи и решим их.
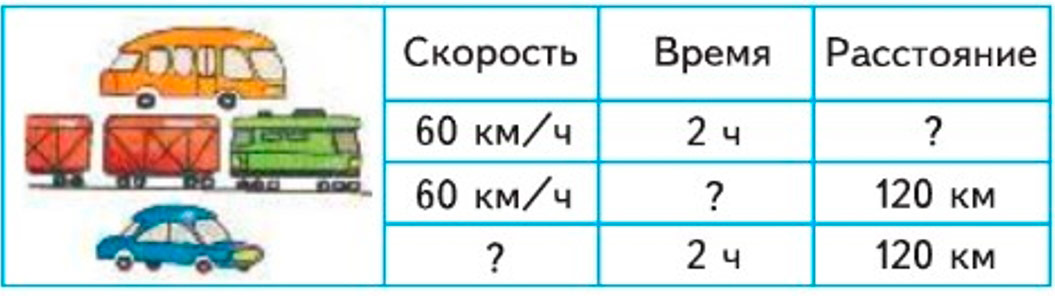
Составим и решим первую задачу, используя формулу из подсказки.
Поезд ехал до турбазы 2 часа со скоростью 60 км/ч. Какое расстояние он прошел за это время?
60 ∙ 2 = 120 (км) – прошел автобус за 2 часа.
Ответ: 120 км.
Составим и решим вторую задачу, используя формулу из подсказки.
Поезд вёз ценный груз до города целых 120 км со скоростью 60 км/ч. Сколько времени понадобилось поезду, чтобы добраться туда?
120 : 60 = 2 (ч) – ехал поезд.
Ответ: 2 часа.
Составим и решим третью задачу, используя формулу из подсказки.
Легковая машина торопилась на автостоянку, расстояние до которой 120 км. С какой скоростью ехала машина, если она была в пути 2 часа?
120 : 2 = 60 (км/ч) – скорость легкового автомобиля.
Ответ: 60 км/ч.
Номер 28.
Объясни, как можно найти:
скорость, зная расстояние и время;
расстояние, зная скорость и время;
время, зная скорость и расстояние.
Чтобы найти скорость, зная расстояние и время, нужно разделить расстояние на время, V = S : t. Чтобы найти расстояние, зная скорость и время, нужно перемножить известные величины, S = V ∙ t. Чтобы найти время, зная скорость и расстояние, нужно расстояние поделить на скорость, t = S : V.
Вспомни формулы нахождения скорости, расстояния и времени.
Как найти скорость.
Чтобы найти скорость, зная расстояние и время, нужно разделить расстояние на время, V = S : t.
Как найти расстояние.
Чтобы найти расстояние, зная скорость и время, нужно перемножить известные величины, S = V ∙ t.
Как найти время.
Чтобы найти время, зная скорость и расстояние, нужно расстояние разделить на скорость, t = S : V.
Номер 29.
1) За 1 ч, двигаясь с одинаковой скоростью, машина проходит 60 км. Сколько километров она пройдёт за 10 мин? 2) Поезд, двигаясь с одинаковой скоростью, прошёл 1 км за 1 мин. За сколько времени он пройдёт 15 км? 60 км? 3) Составь задачу по чертежу и реши её.

1)

1 час = 60 мин 1 км = 1000 м
1-й способ решения:1) 60 ∙ 1000 : 60 = 1000 (м/мин) – скорость машины.
2) 1000 ∙ 10 = 10000 (м) – пройдёт машина за 10 минут.
3) 10000 м = 10 км.
Ответ: 10 км пройдёт машина за 10 минут.
За 1 час машина проходит 60 км. 10 минут – это одна шестая часть часа. Значит машина пройдёт в 6 раз меньше.
1) 60 : 10 = 6(р.) – во столько раз меньше затратит времени.
2) 60 : 6 = 10 (км) – всего пройдёт
Ответ: 10 км пройдёт машина за 10 минут.
2)

1) 15 : 1 = 15 (мин) – потребуются поезду, чтобы пройти расстояние в 15 км.
2) 60 : 1 = 60 (мин) – потребуется поезду, чтобы пройти расстояние в 60 км.
Ответ: 15 минут нужно поезду, чтобы пройти 15 км; и 60 минут нужно поезду, чтобы пройти расстояние в 60 км.
3) Два велосипедиста выехали навстречу друг другу из разных посёлков. Скорость первого велосипедиста – 18 км/ч, а второго – 15 км/ч. До места встречи каждый ехал 3 часа. Каково расстояние между посёлками?
1) 18 ∙ 3 = 54 (км) – проехал первый велосипедист.
2) 15 ∙ 3 = 45 (км) – проехал второй велосипедист.
3) 54 + 45 = 99 (км) – расстояние между посёлками
Ответ: 99 км расстояние между поселками.
1) 18 + 15 = 33 (км) – на какое расстояние они приблизятся за 1 час
2) 33 ∙ 3 = 99 (км) – расстояние между городами
Ответ: 99 км.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Переведем скорость машины в м/мин.
1 час = 60 мин
1 км = 1000 м
1) 60 ∙ 1000 : 60 = 1000 (м/мин) – скорость машины.
Продолжаем рассуждение.
Чтобы узнать, какое расстояние машина пройдет за 10 минут, нужно скорость умножить на время.
2) 1000 ∙ 10 = 10000 (м) – пройдет машина за 10 минут.
3) 10000 м = 10 км.
Записываем ответ.
Ответ: 10 км пройдет машина за 10 минут.
Шаг 1.
Оформляем условие в виде таблицы.

Рассуждаем.
Чтобы узнать, сколько времени потребуется поезду, чтобы преодолеть 15 км, нужно расстояние разделить на скорость.
1) 15 : 1 = 15 (мин) – потребуются поезду, чтобы пройти расстояние в 15 км.
Продолжаем рассуждение.
Чтобы узнать, сколько времени потребуется поезду, чтобы преодолеть 60 км, нужно расстояние разделить на скорость.
2) 60 : 1 = 60 (мин) – потребуется поезду, чтобы пройти расстояние в 60 км.
Записываем ответ.
Ответ: 15 минут и 60 минут.
Шаг 1.
Рассмотрим чертеж и составим по нему задачу.

Два велосипедиста выехали навстречу друг другу из разных поселков. Скорость первого велосипедиста – 18 км/ч, а второго – 15 км/ч. До места встречи каждый ехал 3 часа. Каково расстояние между поселками?
Рассуждаем.
Узнаем, какое расстояние проехал первый велосипедист, для этого скорость умножим на время.
1) 18 ∙ 3 = 54 (км) – проехал первый велосипедист.
Продолжаем рассуждение.
Узнаем, какое расстояние проехал второй велосипедист, для этого скорость умножим на время.
2) 15 ∙ 3 = 45 (км) – проехал второй велосипедист.
Продолжаем рассуждение.
Чтобы узнать, какое расстояние между поселками, нужно сложить расстояния, которые преодолели оба велосипедиста.
3) 54 + 45 = 99 (км)
Записываем ответ.
Ответ: 99 км расстояние между поселками.
Номер 30.
1) За 4 одинаковых велосипеда заплатили k р. Сколько стоят 9 таких велосипедов?
2) Составь задачу по выражению (с : 5) ∙ 3.

1) k : 4 ∙ 9 2) За 5 альбомов заплатили с рублей. Сколько стоят 3 таких альбома?

Повтори, что такое буквенные выражения.
Решим задачу.
Чтобы узнать, сколько стоят 9 велосипедов, для начала нужно узнать, сколько стоит один такой велосипед.
1) k : 4 (р.) − стоит 1 велосипед;
Умножаем стоимость 1-го велосипеда на 9.
2) (k : 4) ∙ 9 (р.) − стоят 9 велосипедов.
Ответ: (k : 4) ∙ 9 (р.)
Составим задачу по выражению (с : 5) ∙ 3.
За 5 альбомов заплатили с рублей. Сколько стоят 3 таких альбома?
Номер 31.
Грузовая машина вышла из посёлка в 7 ч и прибыла в город в 13 ч того же дня. За это время она прошла 240 км. С какой скоростью шла машина?
Ответ:
Время отбытия – 7 ч
Время прибытия – 13 ч
Расстояние – 240 км
Скорость – ? км/ч
1) 13 − 7 = 6 (ч) – машина была в пути.
2) 240 : 6 = 40 (км/ч) - скорость машины
Ответ: 40 км/ч скорость машины.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде краткой записи.
Время отбытия – 7 ч
Время прибытия – 13 ч
Расстояние – 240 км
Скорость – ? км/ч
Рассуждаем.
Узнаем, сколько времени машина была в пути, для этого из времени прибытия вычитаем время отбытия.
1) 13 − 7 = 6 (ч) – машина была в пути.
Продолжаем рассуждение.
Теперь узнаем скорость машины, для этого расстояние разделим на время.
2) 240 : 6 = 40 (км/ч) – скорость машины.
Записываем ответ.
Ответ: 40 км/ч.
Номер 32.
Расстояние от Москвы до Екатеринбурга по железной дороге 1667 км, от Екатеринбурга до Новосибирска 1524 км и от Москвы до Иркутска 5042 км. Чему равно расстояние от Новосибирска до Иркутска по железной дороге?


1) 1 667 + 1 524 = 3 191 (км) – расстояние от Москвы до Новосибирска 2) 5 042 – 3 191 = 1 851 (км) – расстояние от Новосибирска до Иркутска

Ответ: 1 851 км.
2-й способ решения:1) 5 042 – 1 667 = 3 375 (км) – расстояние от Екатеринбурга да Иркутска 2) 3 375 – 1 524 = 1 851 (км) – расстояние от Новосибирска до Иркутска

Ответ: 1 851 км.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Узнаем, какое расстояние от Москвы до Новосибирска.
1) 1667 + 1524 = 3191 (км) – от Москвы до Новосибирска.
Продолжаем рассуждение.
Узнаем, какое расстояние от Новосибирска до Иркутска.
2) 5042 – 3191 = 1851 (км)
Записываем ответ.
Ответ: 1851 км от Новосибирска до Иркутска.
Оформляем задание в тетрадь.

Номер 33.
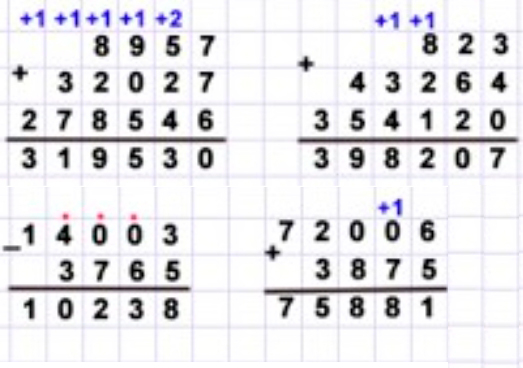
Проверь вычисления на калькуляторе.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем и выполняем вычисление.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч):
278 546 + 8 957 + 32 027.
Складываю единицы:
6 + 7 + 7 = 20. 20 ед. – это 2 дес. и 0 ед.; 0 ед. пишу под единицами, а 2 дес. прибавлю к десяткам.
Складываю десятки:
4 + 5 + 2 = 11, да ещё 2.
11 + 2 = 13.
13 дес. – это 1 сот. и 3 дес.; 3 дес. пишу под десятками, а 1 сот. прибавлю к сотням.
Складываю сотни:
5 + 9 + 0 = 14, да ещё 1.
14 + 1 = 15.
15 сот. – это 1 ед. тыс. и 5 сот.; 5 сот. пишу под сотнями, а 1 ед. тыс. прибавлю к единицам тысяч.
Складываю единицы тысяч:
8 + 8 + 2 = 18, да ещё 1.
18 + 1 = 19.
19 ед. тыс. – это 1 дес. тыс. и 9 ед. тыс.; 9 ед. тыс. пишу под единицами тысяч, а 1 дес. тыс. прибавлю к десяткам тысяч.
Складываю десятки тысяч:
7 + 3 = 10, да ещё 1.
10 + 1 = 11.
11 дес. тыс. – это 1 сот. тыс. и 1 ед. тыс.; 1 дес. тыс. пишу под десятками тысяч, а 1 сот. тыс. прибавлю к сотням тысяч.
Складываю сотни тысяч:
2, да ещё 1.
2 + 1 = 3. Пишу 3 под сотнями тысяч.
Читаю ответ: 319 530.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
Номер 34.
Ответ:3 · (14 + 8) : 2 = 33 1) 14 + 8 = 22 2) 3 · 22 = 3 · (20 + 2) = 60 + 6 = 66 3) 66 : 2 = (60 + 6) : 2 = 30 + 3 = 33

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.
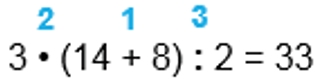
1) 14 + 8 = 22
2) 3 • 22 = 66
3) 66 : 2 = 33
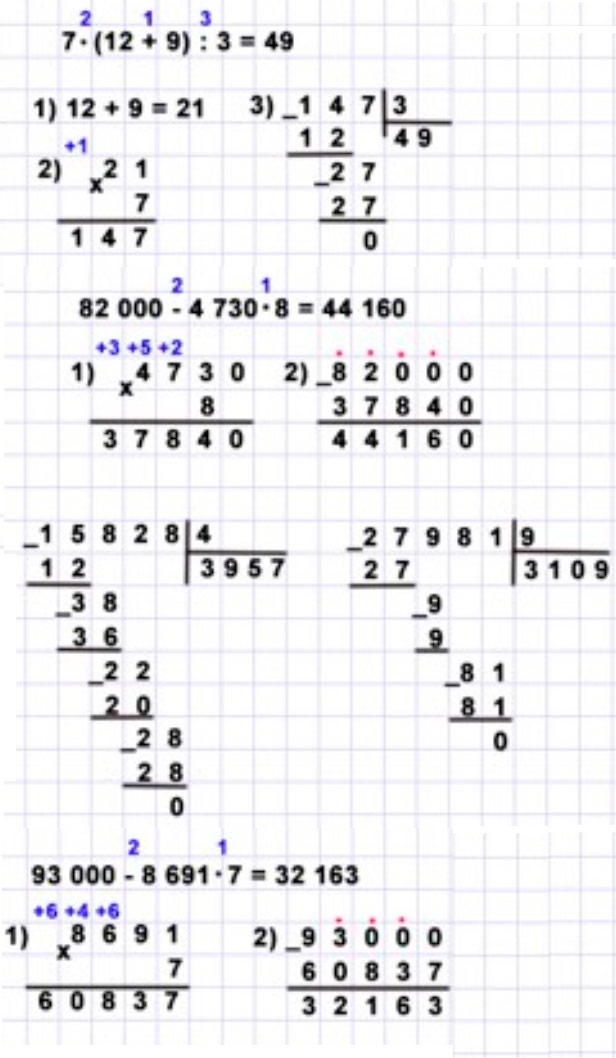
Оформляем задание в тетрадь.
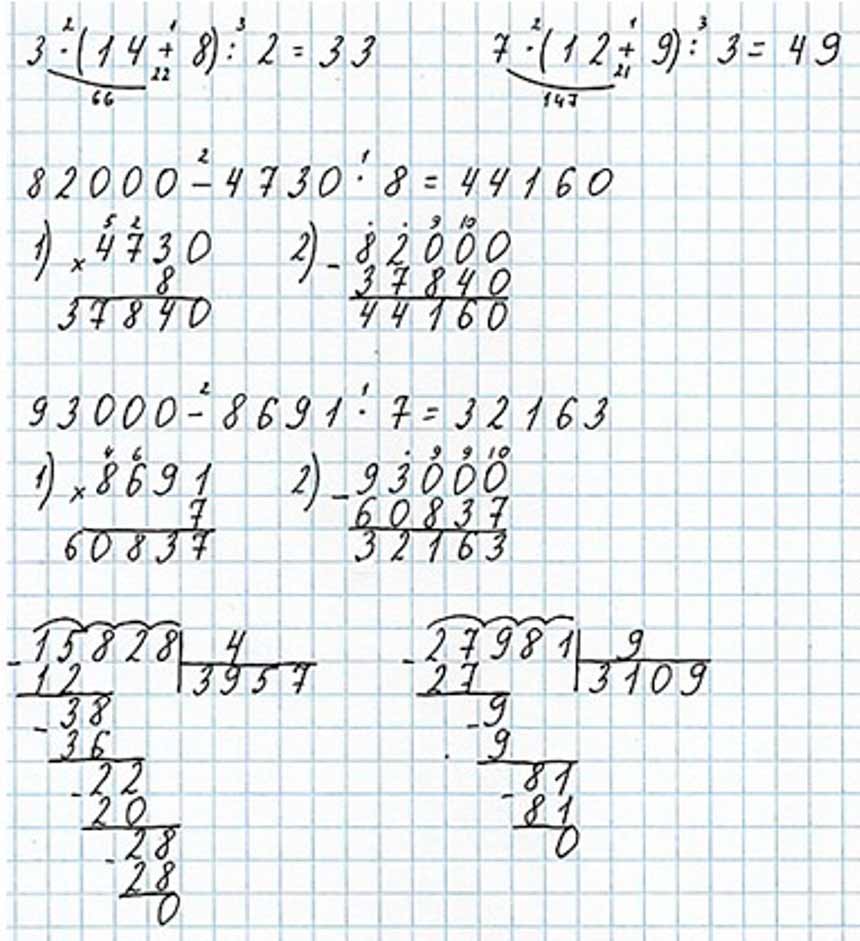
Задание внизу страницы
Проверочные работы с.54 Проверочные работы с.55
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.