Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 34

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 129.
Найди ошибки в вычислениях и реши правильно.


В первом решении ошибка была в том, что второе неполное делимое 45 не смогли разделить, так как оно меньше и сазу снесли следующую цифру, не записав 0 в частном.
Во втором решении ошибка была в том, что третье неполное делимое 600 не разделили, приняв его за остаток.
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Рассмотрим данные примеры и их решения.
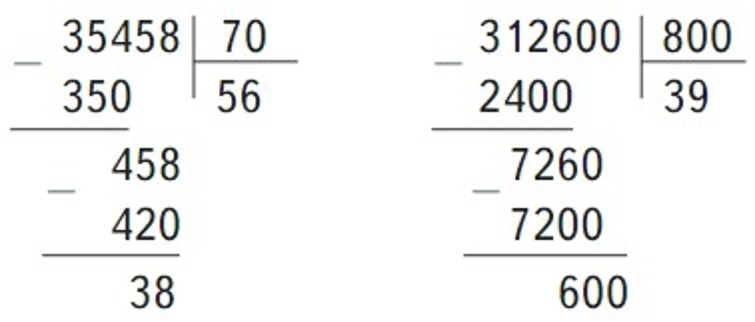
Решим примеры правильно и объясним, в чем была ошибка предыдущего решения.
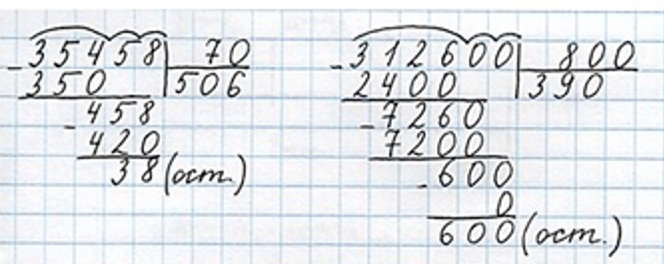
В первом решении ошибка была в том, что второе неполное делимое 45 не смогли разделить, так как оно меньше и сазу снесли следующую цифру, не записав 0 в частном.
Во втором решении ошибка была в том, что третье неполное делимое 600 не разделили, приняв его за остаток.
Номер 130.
Выполни деление с остатком и проверь решение.
Ответ:

Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Вспоминаем как выполнять проверку.
Проверка:
1) Остаток должен быть меньше делителя.
2) Умножим частное на делитель.
3) Прибавим к результату остаток. Сумма должна быть равна делимому.
Выполняем вычисления и оформляем задание в тетрадь.

Номер 131.
В ящике помещается 20 кг моркови. Сколько потребуется таких ящиков, чтобы отправить в магазин 675 кг моркови? Сколько килограммов моркови будет в последнем ящике?
Ответ:1 ящ. – 20 кг ? ящ. – 675 кг 675 : 20 = 33 (ост. 15) 33 целых ящика и 1 ящик, в котором будет только 15 кг.

Ответ: 34 ящика потребуется, но в последнем будет 15 кг.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
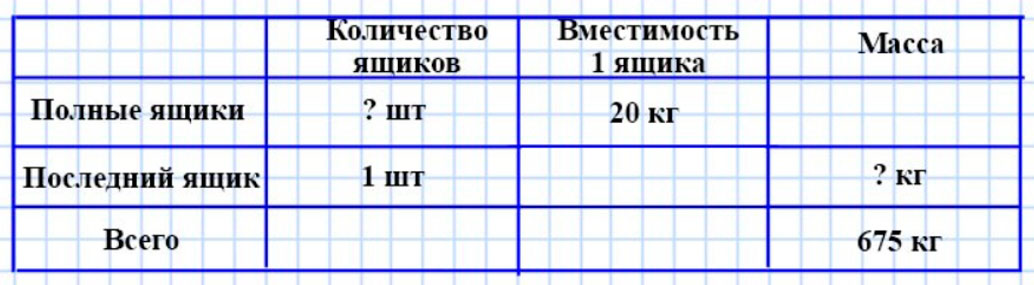
Рассуждаем.
Чтобы узнать, сколько ящиков потребуется для отправки моркови, нужно всю массу моркови разделить на количество килограмм в одном ящике.
675 : 20 = 33 (ост. 15)
33 целых ящика и 1 ящик, в котором будет только 15 кг.
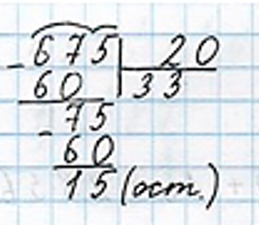
Записываем ответ.
Ответ: 34 ящика потребуется, но в последнем будет 15 кг.
Номер 132.
В каждом ряду кинозала 30 мест. На сеанс продано 942 билета. Сколько полных рядов в этом зале могут занять зрители с билетами?
Ответ:1 ряд – 30 мест ? рядов – 942 б. 942 : 30 = 31 (ост. 12)

Ответ: 31 ряд могут занять.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
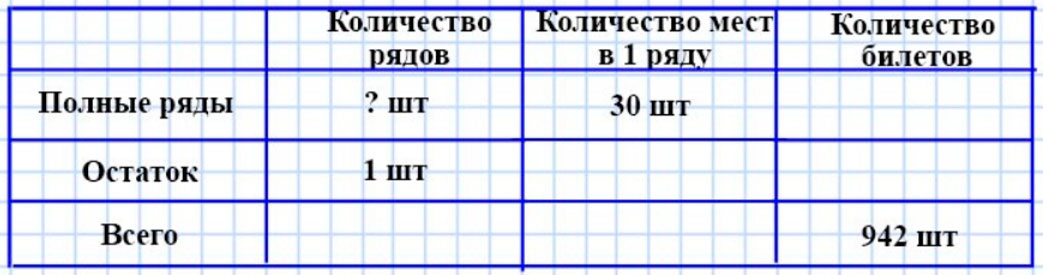
Рассуждаем.
Чтобы узнать, сколько полных рядов могут занять зрители, нужно количество проданных билетов разделить на количество мест в ряду.
942 : 30 = 31 (ост. 12)
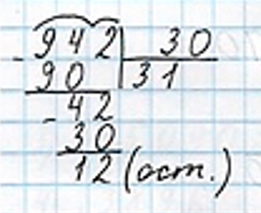
Записываем ответ.
Ответ: 31 ряд могут занять.
Номер 133.
Два лыжника вышли из посёлка одновременно в противоположных направлениях. Один из них шёл со скоростью 12 км/ч, а другой – 10 км/ч. Через сколько часов расстояние между ними будет 44 км? Какое расстояние пройдёт за это время каждый лыжник?
Ответ:

1) 12 + 10 = 22 (км/ч) – скорость удаления лыжников.
2) 44 : 22 = 2 (ч) – будут в пути лыжники.
3) 12 ∙ 2 = 24 (км) – прошёл 1-ый лыжник.
4) 10 ∙ 2 = 20 (км) – прошёл 2-ой лыжник.
Ответ: через 2 часа; первый лыжник – 24 км.; второй лыжник – 20 км.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Рассуждаем и выполняем вычисление.
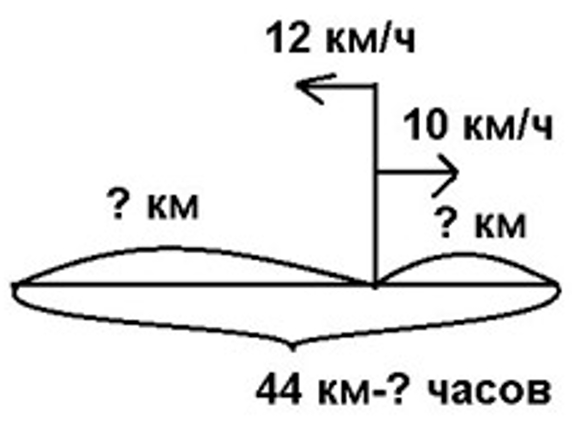
Рассуждаем.
Узнаем общую скорость удаления лыжников.
1) 12 + 10 = 22 (км/ч) – скорость удаления лыжников
Продолжаем рассуждение.
Узнаем, сколько времени лыжники будут в пути, для этого общее расстояние делим на общую скорость.
2) 44 : 22 = 2 (ч) – будут в пути лыжники
Продолжаем рассуждение.
Узнаем, сколько км прошел первый лыжник. Для этого скорость, с которой он двигался, умножим на время в пути.
3) 12 ∙ 2 = 24 (км) – прошёл 1-ый лыжник
Продолжаем рассуждение.
Узнаем, сколько км прошел второй лыжник. Для этого скорость, с которой он двигался, умножим на время в пути.
4) 10 ∙ 2 = 20 (км) – прошёл 2-ой лыжник
Записываем ответ.
Ответ: через 2 часа; 1-ый л. – 24 км.; 2-ой л. – 20 км.
Номер 134.
Из двух посёлков выехали одновременно навстречу друг другу два всадника. Первый ехал со скоростью 200 м/мин, а второй проезжал в минуту на 20 м меньше. Всадники встретились через 50 мин. Найди расстояние между посёлками.
Ответ:
1) 200 − 20 = 180 (м/мин) – скорость второго всадника.
2) 200 + 180 = 380 (м/мин) – скорость сближения.
3) 380 ∙ 50 = 19000 (м) – расстояние между посёлками.
19000 м = 19 км
Ответ:расстояние между посёлками составляет 19 км.
1) 200 − 20 = 180 (м/мин) – скорость второго всадника.
2) 200 · 50 = 10 000 (м) – проехал первый всадник.
3) 180 ∙ 50 = 9000 (м) – проехал второй всадник.
4) 10 000 + 9 000 = 19 000 (м) – расстояние между посёлками.
19000 м = 19 км
Ответ: расстояние между посёлками составляет 19 км.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
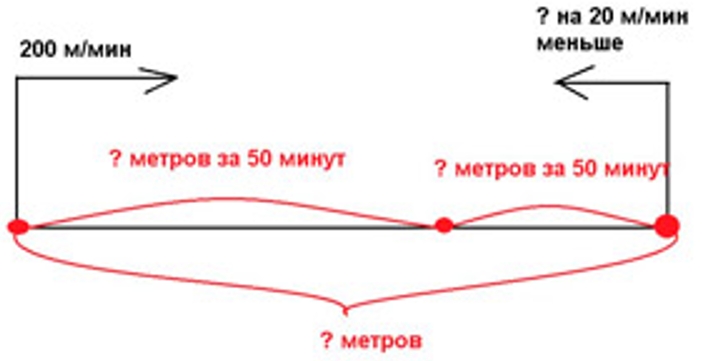
Рассуждаем.
Узнаем скорость второго всадника, для этого из скорости первого всадника вычтем 20 м/мин, потому что известно, что скорость второго на 20 м/мин меньше.
1) 200 − 20 = 180 (м/мин) – скорость второго всадника.
Продолжаем рассуждение.
Найдем скорость сближения всадников, для этого сложим скорости каждого из них вместе.
2) 200 + 180 = 380 (м/мин) – скорость сближения.
Продолжаем рассуждение.
Теперь можем найти расстояние между поселками, для этого скорость сближения всадников умножим на время, через которое они встретились.
3) 380 ∙ 50 = 19000 (м) – расстояние между посёлками.
19000 м = 19 км
Записываем ответ.
Ответ: 19 км.
Номер 135.
Найди значение выражения 120 : 4 + 2 ∙ 3. Измени порядок действий в этом выражении с помощью скобок так, чтобы его значение стало равно 60; 96; 12.
Ответ:120 : 4 + 2 ∙ 3 = 30 + 6 = 36 120 : (4 + 2) ∙ 3 = 120 : 6 · 3 = 20 · 3 = 60 (120 : 4 + 2) ∙ 3 = (30 + 2) · 3 = 32 · 3 = 96 120 : (4 + 2 ∙ 3) = 120 : (4 + 6) = 120 : 10 = 12
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления.
120 : 4 + 2 ∙ 3 = 36
Изменим порядок действий, чтобы получились значения: 60; 96; 12.
120 : (4 + 2) ∙ 3 = 60
(120 : 4 + 2) ∙ 3 = 96
120 : (4 + 2 ∙ 3) = 12
Оформляем задание в тетрадь.
Номер 136.
Выполни деление и проверь умножением.
Ответ:
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисления с пояснениями.
Пишу: 432 240 : 60.
Первое неполное делимое – 432 тысячи. В записи частного будет 4 цифры.
Разделю 432 на 60. Для этого разделю 43 на 6, получу 7 – столько тысяч будет в частном.
Умножу 60 на 7, получу 420 – столько тысяч разделили.
Вычту 420 из 432, получу 12 – столько тысяч осталось разделить.
Сравню остаток с делителем: сотен осталось меньше, чем 60.
Второе неполное делимое – 122 сотни.
Разделю 122 на 60. Для этого разделю 12 на 6, получу 2 – столько сотен будет в частном.
Умножу 60 на 2, получу 120 – столько сотен разделили.
Вычту 120 из 122, получу 2 – столько сотен осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 60.
Третье неполное делимое – 24 десятка.
Разделю 24 на 60. Неполное делимое меньше делителя, поэтому пишу в частном 0.
Добавляем к 24 десяткам 0 единиц, получается 240 единиц.
Разделю 240 на 60. Для этого разделю 24 на 6, получу 4 – столько единиц будет в частном.
Умножу 60 на 4, получу 240 – все единицы разделили.
Читаю ответ: частное равно 1 204.
Чтобы проверить деление умножением, нужно частное умножить на делитель и в результате вычислений должно получится делимое.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
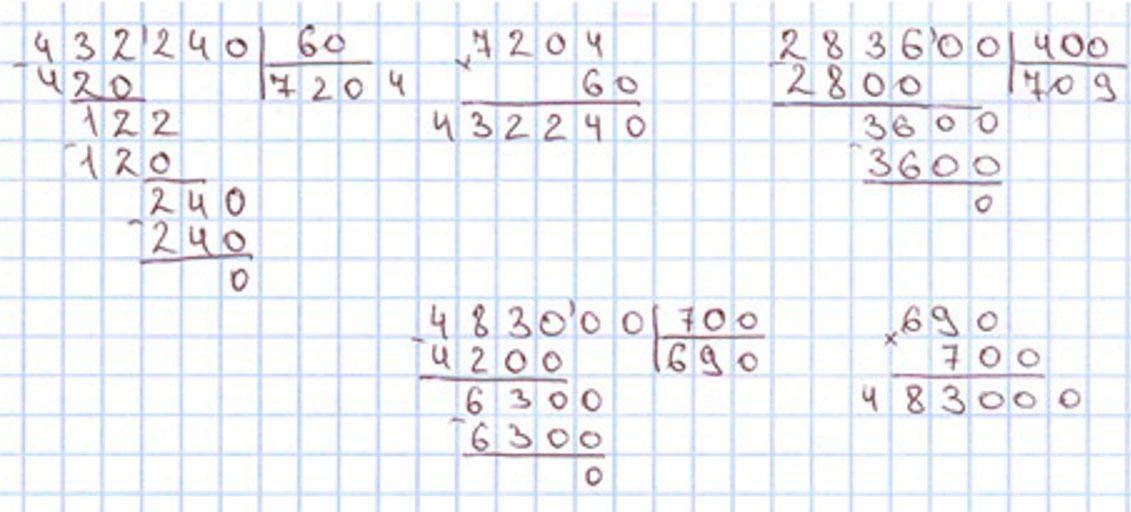
Номер 137.
Ответ:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.

Оставшиеся примеры решаем самостоятельно.
Выполняем вычисления и оформляем задание в тетрадь.

Номер 138.
Ответ:
1 ч − 15 мин = 60 мин − 15 мин = 45 мин
1 сут. − 15 ч = 24 ч − 15 ч = 9 ч
1 т − 8 ц = 10 ц − 8 ц = 2 ц
1 ц − 8 кг = 100 кг − 8 кг = 92 кг
1 м2 − 10 дм2 = 100 дм2 − 10 дм2 = 90 дм2
1 дм2 − 10 см2 = 100 см2 − 10 см2 = 90 см2
Помним о соотношении числовых значений единиц измерения массы:
1 кг = 1000 г
1 ц = 100 кг
1 т = 1000 кг
Помни о соотношении числовых значений единиц измерения площади:
1 см2 = 100 мм2
1 дм2 = 100 см2
1 м2 = 10 000 см2
1 м2 = 100 дм2
Помни о соотношении числовых значений единиц измерения времени:
1 мин = 60 сек
1 час – 60 мин
1 сут = 24 часа
Выполняем вычисления.
1 ч − 15 мин = 60 мин − 15 мин = 45 мин
1 сут. − 15 ч = 24 ч − 15 ч = 9 ч
1 т − 8 ц = 10 ц − 8 ц = 2 ц
1 ц − 8 кг = 100 кг − 8 кг = 92 кг
1 м² − 10 дм² = 100 дм² − 10 дм² = 90 дм²
1 дм² − 10 см² = 100 см² − 10 см² = 90 см²
Оформляем задание в тетрадь.
Задание на полях страницы
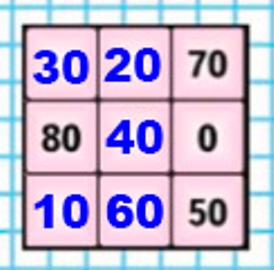
Магический квадрат.

Ответ:

Проверка: 30 + 20 + 70 = 100 + 20 = 120 80 + 40 + 0 = 120 + 0 = 120 10 + 60 + 50 = 70 + 50 = 120 30 + 80 + 10 = 40 + 80 = 120 20 + 40 + 60 = 60 + 60 = 120 70 + 0 + 50 = 120 + 0 = 120 30 + 40 + 50 = 70 + 50 = 120 10 + 40 + 70 = 10 + 110 = 120
Магический квадрат — таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Выполняем вычисления.
70 + 0 + 50 = 120
120 – (80 + 0) = 40
120 – (40 + 50) = 30
120 – (30 + 70) = 20
120 – (20 + 40) = 60
120 – (60 + 50) = 10
Заполняем магический квадрат.
Задание внизу страницы
Задание вверху страницы
1) Объясни решение.
2) Объясни, как более кратко записаны те же вычисления.


425400 : 600
Первое неполное делимое 4254 сотни, значит, в записи частного будет три цифры.
Найду, сколько сотен будет в частном,
Разделю 4254 на 600, для этого разделю 42 на 6, получится 7 – столько сотен будет в частном.
Умножу 600 на 7, получится 4200 – столько сотен разделил.
Вычту 4200 из числа 4254, получится 54 сотни – столько сотен осталось разделить.
Сравню остаток с делителем: сотен осталось меньше, чем 600.
Второе неполное делимое 54 сотни, или 540 десятков.
Найду число десятков в частном: разделю 540 на 600, получится 0 десятков.
Умножу 600 на 0, получится 0.
Вычту 0 из 540, получится 540 десятков – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 600.
Третье неполное делимое 5400.
Разделю 5400 единиц на 600, получится 9.
Умножу 600 на 9, получится 5400, все единицы разделили.
Ответ: 709.
28500 : 30
Первое неполное делимое 285 сотен, значит, в записи частного будет три цифры.
Найду, сколько сотен будет в частном,
Разделю 285 на 30, для этого разделю 28 на 3, получится 9 – столько сотен будет в частном.
Умножу 30 на 9, получится 270 – столько сотен разделил.
Вычту 270 из числа 285, получится 15 сотен – столько сотен осталось разделить.
Сравню остаток с делителем: сотен осталось меньше, чем 30.
Второе неполное делимое 15 сотен, или 150 десятков.
Найду число десятков в частном: разделю 150 на 30, получится 5 десятков.
Умножу 30 на 5, получится 150.
Вычту 150 из 150, получится 0 – все десятки разделили.
Третье неполное делимое 0 единиц.
Разделю 0 единиц на 30, получится 0.
Умножу 0 на 30, получится 0, все единицы разделили.
Ответ: 950.
В остальных случаях рассуждаем аналогично, особое внимание при этом надо уделить записи нулей в частном (не приписывать нули, а получать их делением).
При сокращенной записи если неполное делимое меньше делителя можно просто приписать в частном 0 и списать следующую цифру. В случае, когда в делимом в разряде 0 единиц, а десятки разделены полностью, последний 0 можно не сносить для деления, а списать его в частное.
Помни, как выполнять деление многозначных чисел столбиком на числа, оканчивающиеся нулями.
Рассуждаем.
425400 : 600 = 709

Первое неполное делимое – 4254 сотни. В записи частного будет 3 цифры.
Делим 4254 на 600, для этого 42 делим на 6, получаем 7 – столько сотен будет в частном.
600 ∙ 7 = 4200 – столько сотен разделили
4254 – 4200 = 54 – столько сотен осталось разделить
54 < 600
Второе неполное делимое – 540 десятков.
Делим 540 на 600, для этого 5 делим на 6, получаем 0 – столько десятков будет в частном.
600 ∙ 0 = 0 – столько десятков разделили
540 – 0 = 540 – столько десятков осталось разделить
540 < 600
Третье неполное делимое – 5400 единиц.
Делим 5400 на 600, для этого 54 делим на 6, получаем 9 – столько единиц будет в частном.
600 ∙ 9 = 5400 – разделили все единицы.
Продолжаем рассуждения.
28500 : 30 = 950

Первое неполное делимое – 285 сотен. В записи частного будет 3 цифры.
Делим 285 на 30, для этого 28 делим на 3, получаем 9 – столько сотен будет в частном.
30 ∙ 9 = 270 – столько сотен разделили
285 – 270 = 15 – столько сотен осталось разделить
15 < 30
Второе неполное делимое – 150 десятков.
Делим 150 на 30, для этого 15 делим на 3, получаем 5 – столько десятков будет в частном.
30 ∙ 5 = 150 – столько десятков разделили
150 – 150 = 0 – столько десятков осталось разделить
0 < 30
Третье неполное делимое – 0 единиц.
Делим 0 на 30, получаем 0 – столько единиц будет в частном.
Продолжаем рассуждения.
43600 : 40 = 1090
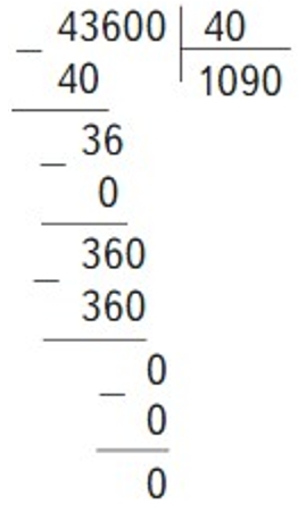
Первое неполное делимое – 43 тысячи. В записи частного будет 4 цифры.
Делим 43 на 40, для этого 4 делим на 4, получаем 1 – столько тысяч будет в частном.
40 ∙ 1 = 40 – столько тысяч разделили
43 – 40 = 3 – столько тысяч осталось разделить
3 < 40
Второе неполное делимое – 36 сотен.
Делим 36 на 40, для этого 3 делим на 4, получаем 0 – столько сотен будет в частном.
40 ∙ 0 = 0 – столько сотен разделили
36 – 0 = 36 – столько сотен осталось разделить
36 < 40
Третье неполное делимое – 360 десятков.
Делим 360 на 40, для этого 36 делим на 4, получаем 9 – столько десятков будет в частном.
40 ∙ 9 = 360 – столько десятков разделили
360 – 360 = 0 – столько десятков осталось разделить
0 < 40
Четвёртое неполное делимое – 0 единиц.
Делим 0 на 40, получаем 0 – столько единиц будет в частном.
Рассмотрим, как более кратко записаны те же примеры.
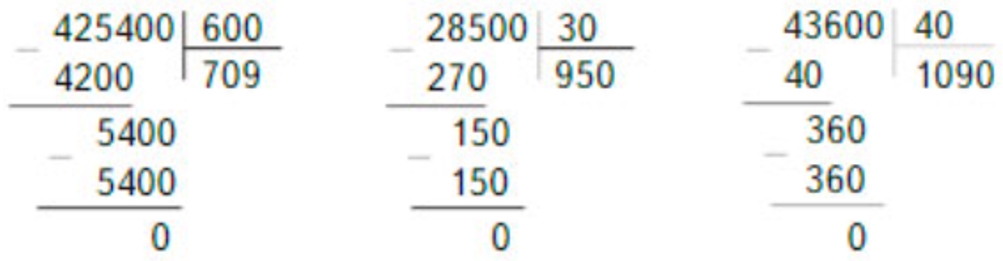
При сокращенной записи, если неполное делимое меньше делителя можно просто приписать в частном 0 и списать следующую цифру. В случае, когда в делимом в разряде 0 единиц, а десятки разделены полностью, последний 0 можно не сносить для деления, а списать его в частное.
Номер 125.
Реши, записывая вычисления подробно или кратко.
Ответ:
Помни, как выполнять деление многозначных чисел столбиком на числа, оканчивающиеся нулями.
Выполняем вычисления.
35210 : 70 = 503
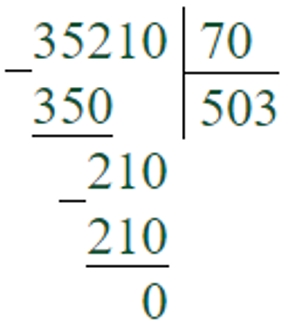
Первое неполное делимое – 352 сотни. В записи частного будет 3 цифры.
Делим 352 на 70, для этого 35 делим на 7, получаем 5 – столько сотен будет в частном.
70 ∙ 5 = 350 – столько сотен разделили
352 – 350 = 2 – столько сотен осталось разделить
2 < 70
Второе неполное делимое – 21 десяток.
21 < 70, поэтому получаем 0 – столько десятков будет в частном.
Третье неполное делимое – 210 единиц.
Делим 210 на 70, для этого 21 делим на 7, получаем 3 – столько единиц будет в частном.
70 ∙ 3 = 210 – разделили все единицы.
40150 : 50 = 803
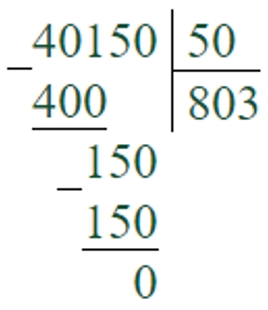
Первое неполное делимое – 401 сотня. В записи частного будет 3 цифры.
Делим 401 на 50, для этого 40 делим на 5, получаем 8 – столько сотен будет в частном.
50 ∙ 8 = 400 – столько сотен разделили
401 – 400 = 1 – столько сотен осталось разделить
1 < 50
Второе неполное делимое – 15 десятков.
15 < 50, поэтому получаем 0 – столько десятков будет в частном.
Третье неполное делимое – 150 единиц.
Делим 150 на 50, для этого 15 делим на 5, получаем 3 – столько единиц будет в частном.
50 ∙ 3 = 150 – разделили все единицы.
168000 : 400 = 420
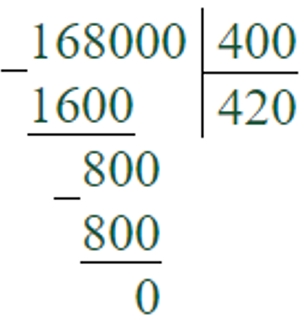
Первое неполное делимое – 1680 сотен. В записи частного будет 3 цифры.
Делим 1680 на 400, для этого 16 делим на 4, получаем 4 – столько сотен будет в частном.
400 ∙ 4 = 1600 – столько сотен разделили
1680 – 1600 = 80 – столько сотен осталось разделить
80 < 400
Второе неполное делимое – 800 десятков.
Делим 800 на 400, для этого 8 делим на 4, получаем 2 – столько десятков будет в частном.
400 ∙ 2 = 800 – разделили все десятки.
Так как все десятки разделили, а в делимом в разряде единиц – 0, то получаем 0 – столько единиц будет в частном.
258000 : 300 = 860
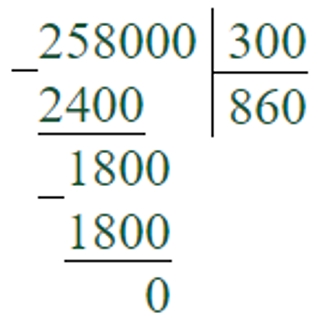
Первое неполное делимое – 2580 сотен. В записи частного будет 3 цифры.
Делим 2580 на 300, для этого 25 делим на 3, получаем 8 – столько сотен будет в частном.
300 ∙ 8 = 2400 – столько сотен разделили
2580 – 2400 = 180 – столько сотен осталось разделить
180 < 300
Второе неполное делимое – 1800 десятков.
Делим 1800 на 300, для этого 18 делим на 3, получаем 6 – столько десятков будет в частном.
300 ∙ 6 = 1800 – разделили все десятки.
Так как все десятки разделили, а в делимом в разряде единиц – 0, то получаем 0 – столько единиц будет в частном.
456000 : 400 = 1140
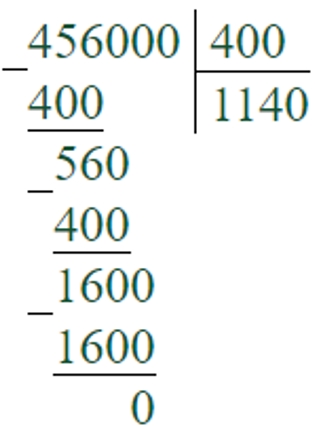
Первое неполное делимое – 456 тысяч. В записи частного будет 4 цифры.
Делим 456 на 400, для этого 4 делим на 4, получаем 1 – столько сотен будет в частном.
400 ∙ 1 = 400 – столько тысяч разделили
456 – 400 = 56 – столько тысяч осталось разделить
56 < 400
Второе неполное делимое – 560 сотен.
Делим 560 на 400, для этого 5 делим на 4, получаем 1 – столько сотен будет в частном.
400 ∙ 1 = 400 – столько сотен разделили
560 – 400 = 160 – столько сотен осталось разделить
160 < 400
Третье неполное делимое – 1600 десятков.
Делим 1600 на 400, для этого 16 делим на 4, получаем 4 – столько десятков будет в частном.
400 ∙ 4 = 1600 – разделили все десятки.
Так как все десятки разделили, а в делимом в разряде единиц – 0, то получаем 0 – столько единиц будет в частном.
260100 : 900 = 289
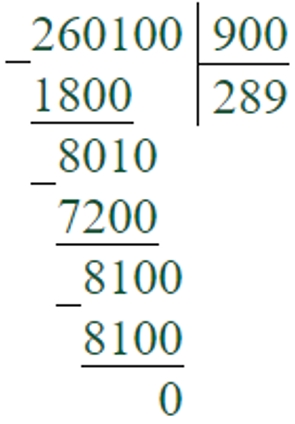
Первое неполное делимое – 2601 сотня. В записи частного будет 3 цифры.
Делим 2601 на 900, для этого 26 делим на 9, получаем 2 – столько сотен будет в частном.
900 ∙ 2 = 1800 – столько сотен разделили
2601 – 1800 = 801 – столько сотен осталось разделить
801 < 900
Второе неполное делимое – 8010 десятков.
Делим 8010 на 900, для этого 80 делим на 9, получаем 8 – столько десятков будет в частном.
900 ∙ 8 = 7200 – столько десятков разделили
8010 – 7200 = 810 – столько десятков осталось разделить
810 < 900
Третье неполное делимое – 8100 единиц.
Делим 8100 на 900, для этого 81 делим на 9, получаем 9 – столько единиц будет в частном.
900 ∙ 9 = 8100 – разделили все единицы.
Оформляем задание в тетрадь.

Номер 126.
Выполни деление с остатком.
Ответ:
1) Помни, как выполнять деление многозначных чисел столбиком на числа, оканчивающиеся нулями.
2) Помни, как выполнять деление с остатком.
Выполняем вычисления.
83056 : 40 = 2076 (ост. 16)
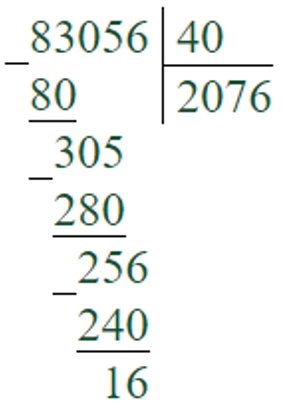
Первое неполное делимое – 83 тысячи. В записи частного будет 4 цифры.
Делим 83 на 40, для этого 8 делим на 4, получаем 2 – столько тысяч будет в частном.
40 ∙ 2 = 80 – столько тысяч разделили
83 – 80 = 3 – столько тысяч осталось разделить
3 < 40
Второе неполное делимое – 30 сотен.
30 < 40, поэтому получаем 0 – столько сотен будет в частном.
Третье неполное делимое – 305 десятков.
Делим 305 на 40, для этого 30 делим на 4, получаем 7 – столько десятков будет в частном.
40 ∙ 7 = 280 – столько десятков разделили
305 – 280 = 25 – столько десятков осталось разделить
25 < 40
Четвёртое неполное делимое – 256 единиц.
Делим 256 на 40, для этого 25 делим на 4, получаем 6 – столько единиц будет в частном.
40 ∙ 6 = 240 – столько единиц разделили
256 – 240 = 16 – столько единиц осталось разделить
Но 16 < 40, поэтому остаток – 16.
48179 : 80 = 602 (ост. 19)
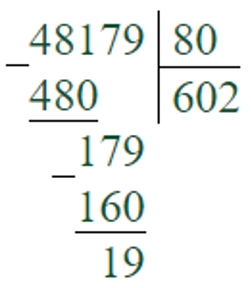
Первое неполное делимое – 481 сотня. В записи частного будет 3 цифры.
Делим 481 на 80, для этого 48 делим на 8, получаем 6 – столько сотен будет в частном.
80 ∙ 6 = 480 – столько сотен разделили
481 – 480 = 1 – столько сотен осталось разделить
1 < 80
Второе неполное делимое – 17 десятков.
17 < 80, поэтому получаем 0 – столько десятков будет в частном.
Третье неполное делимое – 179 единиц.
Делим 179 на 80, для этого 17 делим на 8, получаем 2 – столько единиц будет в частном.
80 ∙ 2 = 160 – столько единиц разделили
179 – 160 = 19 – столько единиц осталось разделить
Но 19 < 80, поэтому остаток – 19.
80630 : 200 = 403 (ост. 30)
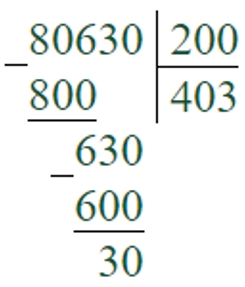
Первое неполное делимое – 806 сотен. В записи частного будет 3 цифры.
Делим 806 на 200, для этого 8 делим на 2, получаем 4 – столько сотен будет в частном.
200 ∙ 4 = 800 – столько сотен разделили
806 – 800 = 6 – столько сотен осталось разделить
6 < 200
Второе неполное делимое – 63 десятка.
63 < 200, поэтому получаем 0 – столько десятков будет в частном.
Третье неполное делимое – 630 единиц.
Делим 630 на 200, для этого 6 делим на 2, получаем 3 – столько единиц будет в частном.
200 ∙ 3 = 600 – столько единиц разделили
630 – 600 = 30 – столько единиц осталось разделить
Но 30 < 200, поэтому остаток – 30.
216349 : 700 = 309 (ост. 49)
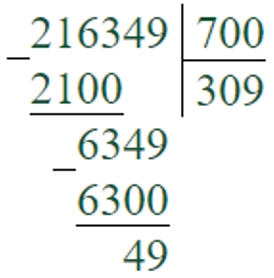
Первое неполное делимое – 2163 сотни. В записи частного будет 3 цифры.
Делим 2163 на 700, для этого 21 делим на 7, получаем 3 – столько сотен будет в частном.
700 ∙ 3 = 2100 – столько сотен разделили
2163 – 2100 = 63 – столько сотен осталось разделить
63 < 700
Второе неполное делимое – 634 десятка.
634 < 700, поэтому получаем 0 – столько десятков будет в частном.
Третье неполное делимое – 6349 единиц.
Делим 6349 на 700, для этого 63 делим на 7, получаем 9 – столько единиц будет в частном.
700 ∙ 9 = 6300 – столько единиц разделили
6349 – 6300 = 49 – столько единиц осталось разделить
Но 49 < 700, поэтому остаток – 49.
Оформляем задание в тетрадь.
83056 : 40 = 2076 (ост. 16)
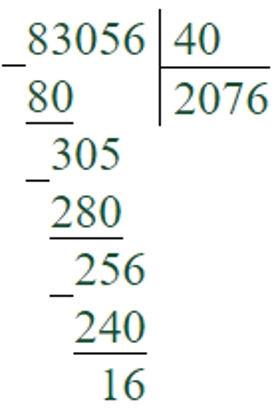
48179 : 80 = 602 (ост. 19)
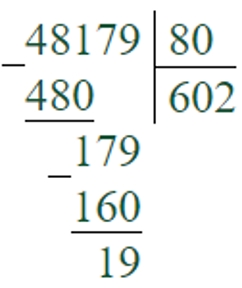
80630 : 200 = 403 (ост. 30)
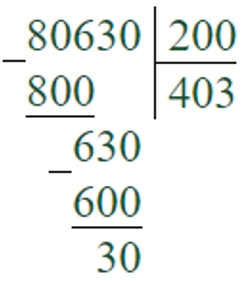
216349 : 700 = 309 (ост. 49)
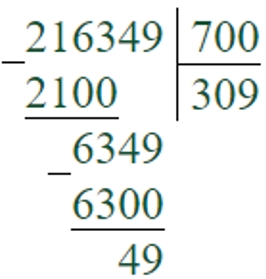
Номер 127.
Два пловца одновременно поплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывёт второй пловец, когда первый проплывёт 270 м? Сделай схематический чертёж и реши задачу. Составь и реши задачи, обратные данной.
Ответ:
1) 270 : 90 = 3 (мин) – время заплыва 1-ого пловца.
2) 40 ∙ 3 = 120 (м) – проплывёт 2-ой пловец.
Ответ: 120 метров в этот момент проплывёт второй пловец.
Обратная задача 1:
Два пловца спрыгнули одновременно с лодки и проплыли по реке в противоположных направлениях: первый проплыл 270 м, второй – 120 м. С какой скоростью плыл второй пловец, если скорость первого – 90 м/мин?
1) 270 : 90 = 3 (мин) – время проплыва 1-ого пловца.
2) 120 : 3 = 40 (м/мин) – скорость 2-ого пловца.
Ответ: скорость второго пловца составляет 40 м/мин.
Обратная задача 2:
Два пловца спрыгнули одновременно с лодки и проплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывет первый спортсмен, когда второй спортсмен проплывет 120 м?
1) 120 : 40 = 3 (мин) – время проплыва 2-ого пловца.
2) 90 ∙ 3 = 270 (м) – проплывёт 1-ый пловец.
Ответ: 270 метров на тот момент проплывёт первый пловец.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Оформляем условие в виде схематического чертежа.
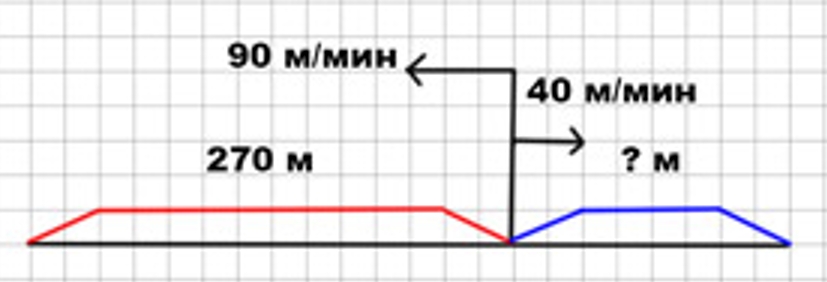
Рассуждаем.
Узнаем время заплыва одного пловца. Для этого расстояние разделим на скорость, с которой он двигался.
270 : 90 = 3 (мин) – время заплыва 1-ого пловца.
Продолжаем рассуждение.
Узнаем, сколько метров проплывет второй пловец. Для этого скорость, с которой он двигался, умножим на время заплыва одного пловца.
40 ∙ 3 = 120 (м) – проплывёт 2-ой пловец.
Записываем ответ.
Ответ: 120 метров проплывёт второй пловец.
Шаг 1.
Составляем задачу.
Два пловца спрыгнули одновременно с лодки и проплыли по реке в противоположных направлениях: первый проплыл 270 м, второй – 120 м. С какой скоростью плыл второй пловец, если скорость первого – 90 м/мин?
Рассуждаем.
Узнаем время заплыва первого пловца. Для этого расстояние разделим на скорость, с которой он двигался.
270 : 90 = 3 (мин) – время заплыва 1-ого пловца.
Продолжаем рассуждение.
Узнаем, скорость второго пловца. Для этого расстояние, которое преодолел второй пловец разделить на время заплыва одного пловца.
120 : 3 = 40 (м/мин) – скорость 2-ого пловца.
Записываем ответ.
Ответ: со скоростью 40 м/мин плыл второй пловец.
Шаг 1.
Составляем задачу.
Два пловца спрыгнули одновременно с лодки и проплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывет первый спортсмен, когда второй спортсмен проплывет 120 м?
Рассуждаем.
Узнаем время заплыва второго пловца. Для этого расстояние разделим на скорость, с которой он двигался.
120 : 40 = 3 (мин) – время заплыва 2-ого пловца.
Продолжаем рассуждение.
Чтобы узнать, сколько метров проплывет второй пловец, нужно скорость его движения умножить на время.
90 ∙ 3 = 270 (м) – проплывёт 1-ый пловец.
Записываем ответ.
Ответ: 270 метров проплывёт первый пловец.
Номер 128.
Реши уравнения.
Ответ:
х : 5 = 1400 − 900
х : 5 = 500
х = 500 ∙ 5
х = 2500
2500 : 5 = 1400 − 900
500 = 500
Ответ: х = 2500.
х − 30 = 1000 − 200
х − 30 = 800
х = 800 + 30
х = 830
830 − 30 = 1000 − 200
800 = 800
Ответ: х = 830.
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Рассуждаем.
х : 5 = 1400 – 900
Произведём вычисления в правой части уравнения.
х : 5 = 500
Чтобы найти делимое, нужно частное умножить на делитель.
х = 500 ∙ 5
х = 2500
Проверка:
Чтобы сделать проверку, нужно найденное значение подставить в уравнение.
2500 : 5 = 1400 – 900
500 = 500 – верно
Продолжаем рассуждения.
х – 30 = 1000 – 200
Произведём вычисления в правой части уравнения.
х – 30 = 800
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
х = 800 + 30
х = 830
Проверка:
Чтобы сделать проверку, нужно найденное значение подставить в уравнение.
830 – 30 = 1000 – 200
800 = 800 – верно
Оформляем задание в тетрадь.
1) х : 5 = 1400 – 900
х : 5 = 500
х = 500 ∙ 5
х = 2500
2) х – 30 = 1000 – 200
х – 30 = 800
х = 800 + 30
х = 830
Номер 129.
Расставь знаки действий и скобки так, чтобы получились верные равенства.
Ответ:
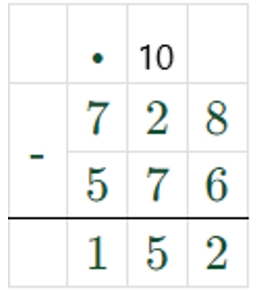
728 − (72 ∙ 8) = 152
728 − 72 : 8 = 719
(728 + 72) : 8 = 100
728 + 72 : 8 = 737
1) Помним о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем.
728 ◯ 72 ◯ 8 = 152
Расставим знаки и скобки.
728 − (72 ∙ 8) = 152
Проверим, верно ли равенство, выполнив вычисление по действиям.
1) 72 ∙ 8 = 576
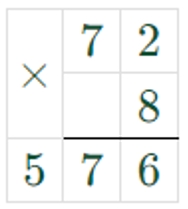
2) 728 – 576 = 152
Продолжаем рассуждения.
728 ◯ 72 ◯ 8 = 719
Расставим знаки.
728 − 72 : 8 = 719
Проверим, верно ли равенство, выполнив вычисление по действиям.
1) 72 : 8 = 9
2) 728 – 9 = 719
Продолжаем рассуждения.
728 ◯ 72 ◯ 8 = 100
Расставим знаки и скобки.
(728 + 72) : 8 = 100
Проверим, верно ли равенство, выполнив вычисление по действиям.
1) 728 + 72 = 700 + 28 + 72 = 700 + 100 = 800
2) 800 : 8 = 8 сот. : 8 = 1 сот. = 100
Продолжаем рассуждения.
728 ◯ 72 ◯ 8 = 737
Расставим знаки.
728 + 72 : 8 = 737
Проверим, верно ли равенство, выполнив вычисление по действиям.
1) 72 : 8 = 9
2) 728 + 9 = 737
Оформляем задание в тетрадь.
728 − (72 ∙ 8) = 152
728 − 72 : 8 = 719
(728 + 72) : 8 = 100
728 + 72 : 8 = 737
Задание внизу страницы
Выполни деление с остатком.
Ответ:
1) Помни, как выполнять деление многозначных чисел столбиком на числа, оканчивающиеся нулями.
2) Помни, как выполнять деление с остатком.
Выполняем вычисления.
438500 : 700 = 626 (ост. 300)
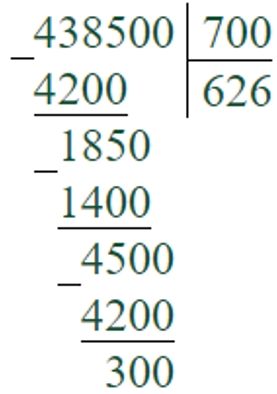
Первое неполное делимое – 4385 сотен. В записи частного будет 3 цифры.
Делим 4385 на 700, для этого 43 делим на 7, получаем 6 – столько сотен будет в частном.
700 ∙ 6 = 4200 – столько сотен разделили
4385 – 4200 = 185 – столько сотен осталось разделить
185 < 700
Второе неполное делимое – 1850 десятков.
Делим 1850 на 700, для этого 18 делим на 7, получаем 2 – столько десятков будет в частном.
700 ∙ 2 = 1400 – столько десятков разделили
1850 – 1400 = 450 – столько десятков осталось разделить
450 < 700
Третье неполное делимое – 4500 единиц.
Делим 4500 на 700, для этого 45 делим на 7, получаем 6 – столько единиц будет в частном.
700 ∙ 6 = 4200 – столько единиц разделили
4500 – 4200 = 300 – столько единиц осталось разделить
Но 300 < 700, поэтому остаток – 300.
Оформляем задание в тетрадь.
438500 : 700 = 626 (ост. 300)
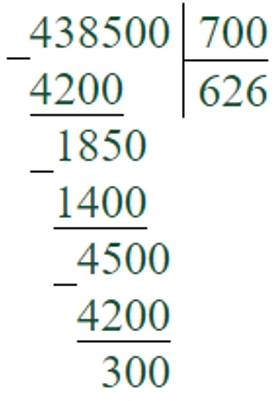
Задание на полях страницы
Магический квадрат.


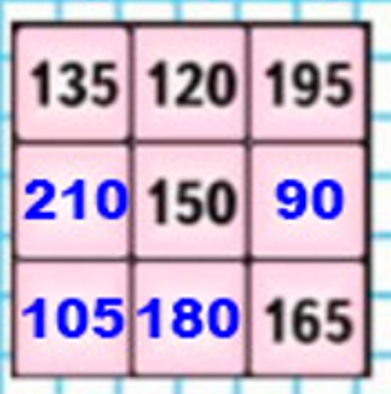
Проверка: 135 + 120 + 195 = 330 + 120 = 450 210 + 150 + 90 = 300 + 150 = 450 105 + 180 + 165 = 270 + 180 = 450 135 + 210 + 105 = 240 + 210 = 450 120 + 150 + 180 = 300 + 150 = 450 195 + 90 + 165 = 360 + 90 = 450 135 + 150 + 165 = 300 + 150 = 450 105 + 150 + 195 = 150 + 300 = 450
Магический квадрат – квадрат, в котором все числа на одной линии в сумме по горизонтали, вертикали и диагонали образуют в сумме одно и то же число.
Рассуждаем.
Чтобы узнать, какая сумма должна быть на каждой линии, сложим имеющиеся числа по диагонали.
135 + 150 + 165 = 100 + 100 + 100 + 35 + 50 + 65 = 300 + 150 = 450
Рассмотрим первую строку.
135 + ☐ + 195 = 450
В строке не хватает второго числа.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
450 – (135 + 195) = 450 – 330 = 120
120 – недостающее число в первой строке.
Продолжаем рассуждения.
Рассмотрим третий столбец.
195 + ☐ + 165 = 450
В столбце не хватает второго числа.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
450 – (195 + 165) = 450 – 360 = 90
90 – недостающее число в третьем столбце.
Продолжаем рассуждения.
Рассмотрим вторую строку.
☐ + 150 + 90 = 450
В строчке не хватает первого числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
450 – (150 + 90) = 450 – 240 = 210
210 – недостающее число во второй строке.
Продолжаем рассуждения.
Рассмотрим второй столбец.
120 + 150 + ☐ = 450
В столбце не хватает третьего числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
450 – (120 + 150) = 450 – 270 = 180
180 – недостающее число во втором столбце.
Продолжаем рассуждения.
Рассмотрим первый столбец.
135 + 210 + ☐ = 450
В столбце не хватает третьего числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
450 – (135 + 210) = 450 – 345 = 105
105 – недостающее число в первом столбце.
Запишем недостающие числа в квадрат.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.