Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 30

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 109.
Объясни по записи, как выполнили деление 3570 : 90. Назови частное и остаток.
Ответ:
3570 : 90 = 39 (ост. 60)
Объяснение:
Первое неполное делимое – 357 десятков. В записи частного будет 2 цифры.
Разделю 357 на 90. Для этого разделю 35 на 9, получу 3 – столько десятков будет в частном.
Умножу 90 на 3, получу 270 – столько десятков разделили.
Вычту 270 из 357, получу 87 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 90.
Второе неполное делимое – 870 единиц.
Разделю 870 на 90. Для этого разделю 87 на 9, получу 9 – столько единиц будет в частном.
Умножу 90 на 9, получу 810.
Вычту 810 из 870, получу 60 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 90.
Читаю ответ: частное равно 39, остаток 60.
Краткий ответ:
Деление выполнено так: попробуем по 3.
3 умножить на 90 будет 270.
357 минус 270 будет 87 сносим ноль.
Попробуем по 9. 9 умножить на 90 будет 810.
870 минус 810 будет 60, и это остаток, а 39 – неполное частное.
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисление.
3570 : 90 = 39 (ост. 60)
Объясняем вычисление.
Первое неполное делимое – 357 десятков. В записи частного будет 2 цифры.
Разделю 357 на 90. Для этого разделю 35 на 9, получу 3 – столько десятков будет в частном.
Умножу 90 на 3, получу 270 – столько десятков разделили.
Вычту 270 из 357, получу 87 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 90.
Второе неполное делимое – 870 единиц.
Разделю 870 на 90. Для этого разделю 87 на 9, получу 9 – столько единиц будет в частном.
Умножу 90 на 9, получу 810.
Вычту 810 из 870, получу 60 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 90.
Читаю ответ: частное равно 39, остаток 60.
Номер 110.
Ответ:
В примере 360 : 60 - 20 : 1 опечатка. Вместо знака "-" должен быть "+".

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисление с пояснением.
Пишу: 6020 : 70.
Первое неполное делимое – 602 десятка. В записи частного будет 2 цифры.
Разделю 602 на 70. Для этого разделю 60 на 7, получу 8 – столько десятков будет в частном.
Умножу 70 на 8, получу 560 – столько десятков разделили.
Вычту 560 из 602, получу 42 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 70.
Второе неполное делимое – 420 единиц.
Разделю 420 на 70. Для этого разделю 42 на 7, получу 6 – столько единиц будет в частном.
Умножу 70 на 6, получу 420 – все единицы разделили.
Читаю ответ: частное равно 86.
Далее рассуждаю аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
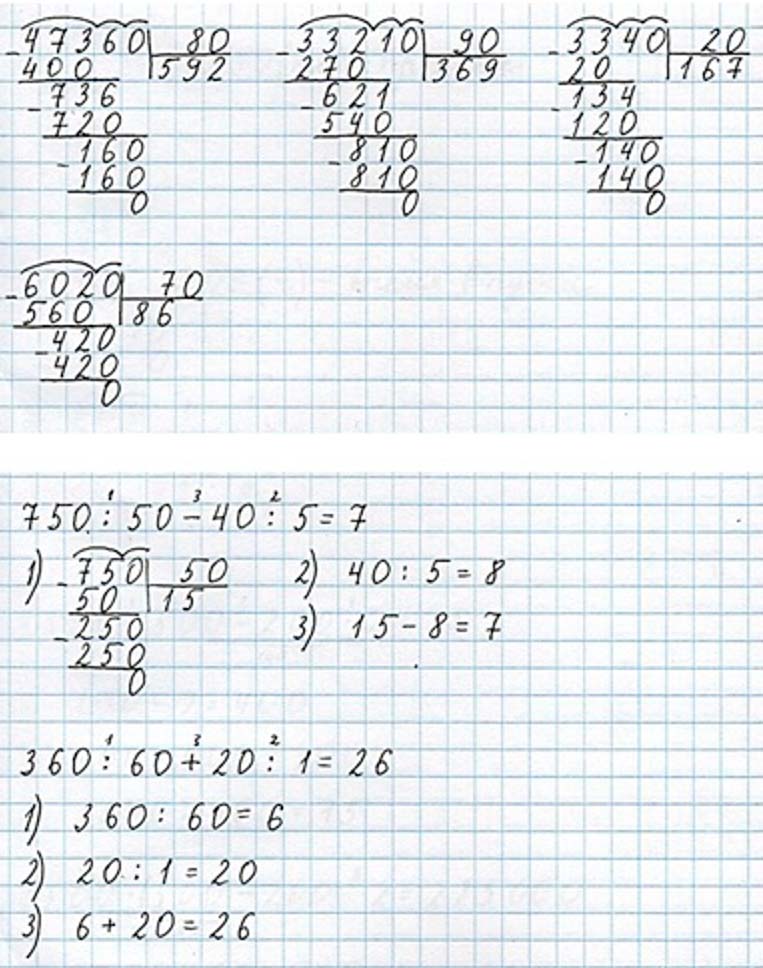
Номер 111.
Выполни деление с остатком.
Ответ:
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Выполняем вычисление с пояснениями.
Пишу: 7 940 : 40.
Первое неполное делимое – 79 сотен. В записи частного будет 3 цифры.
Разделю 79 на 40. Для этого разделю 7 на 4, получу 1 – столько сотен будет в частном.
Умножу 40 на 1, получу 40 – столько сотен разделили.
Вычту 40 из 79, получу 39 – столько сотен осталось разделить.
Сравню остаток с делителем: сотен осталось меньше, чем 40.
Второе неполное делимое – 394 десятка.
Разделю 394 на 40. Для этого разделю 39 на 4, получу 9 – столько десятков будет в частном.
Умножу 40 на 9, получу 360 – столько десятков разделили.
Вычту 360 из 394, получу 34 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 40.
Третье неполное делимое– 340 единиц.
Разделю 340 на 40. Для этого разделю 34 на 4, получу 8 – столько единиц будет в частном.
Умножу 40 на 8, получу 320 – столько единиц разделили.
Вычту 320 из 340, получу 20 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 40.
Читаю ответ: частное равно 198, остаток 20.
Пишу: 6 780 : 90.
Первое неполное делимое – 678 десятков. В записи частного будет 2 цифры.
Разделю 678 на 90. Для этого разделю 67 на 9, получу 7 – столько десятков будет в частном.
Умножу 90 на 7, получу 630 – столько десятков разделили.
Вычту 630 из 678, получу 48 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 90.
Второе неполное делимое – 480 единиц.
Разделю 480 на 90. Для этого разделю 48 на 9, получу 5 – столько единиц будет в частном.
Умножу 90 на 5, получу 450 – столько единиц разделили.
Вычту 450 из 480, получу 30 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 90.
Читаю ответ: частное равно 75, остаток 30.
Пишу: 47 350 : 60.
Первое неполное делимое – 473 сотен. В записи частного будет 3 цифры.
Разделю 473 на 60. Для этого разделю 47 на 6, получу 7 – столько сотен будет в частном.
Умножу 60 на 7, получу 420 – столько сотен разделили.
Вычту 420 из 473, получу 53 – столько сотен осталось разделить.
Сравню остаток с делителем: сотен осталось меньше, чем 60.
Второе неполное делимое – 535 десятка.
Разделю 535 на 60. Для этого разделю 53 на 6, получу 8 – столько десятков будет в частном.
Умножу 60 на 8, получу 480 – столько десятков разделили.
Вычту 480 из 535, получу 55 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 60.
Третье неполное делимое – 550 единиц.
Разделю 550 на 60. Для этого разделю 55 на 6, получу 9 – столько единиц будет в частном.
Умножу 60 на 9, получу 540 – столько единиц разделили.
Вычту 540 из 550, получу 10 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 60.
Читаю ответ: частное равно 789, остаток 10.
Пишу: 23 070 : 40.
Первое неполное делимое – 230 сотен. В записи частного будет 3 цифры.
Разделю 230 на 40. Для этого разделю 23 на 4, получу 5 – столько сотен будет в частном.
Умножу 40 на 5, получу 200 – столько сотен разделили.
Вычту 200 из 230, получу 30 – столько сотен осталось разделить.
Сравню остаток с делителем: сотен осталось меньше, чем 40.
Второе неполное делимое – 307 десятков.
Разделю 307 на 40. Для этого разделю 30 на 4, получу 7 – столько десятков будет в частном.
Умножу 40 на 7, получу 280 – столько десятков разделили.
Вычту 280 из 307, получу 27 – столько десятков осталось разделить.
Сравню остаток с делителем: десятков осталось меньше, чем 40.
Третье неполное делимое – 270 единиц.
Разделю 270 на 40. Для этого разделю 27 на 4, получу 6 – столько единиц будет в частном.
Умножу 40 на 6, получу 240 – столько единиц разделили.
Вычту 240 из 270, получу 30 – столько единиц осталось разделить.
Сравню остаток с делителем: единиц осталось меньше, чем 40.
Читаю ответ: частное равно 576, остаток 40.
Оформляем задание в тетрадь.
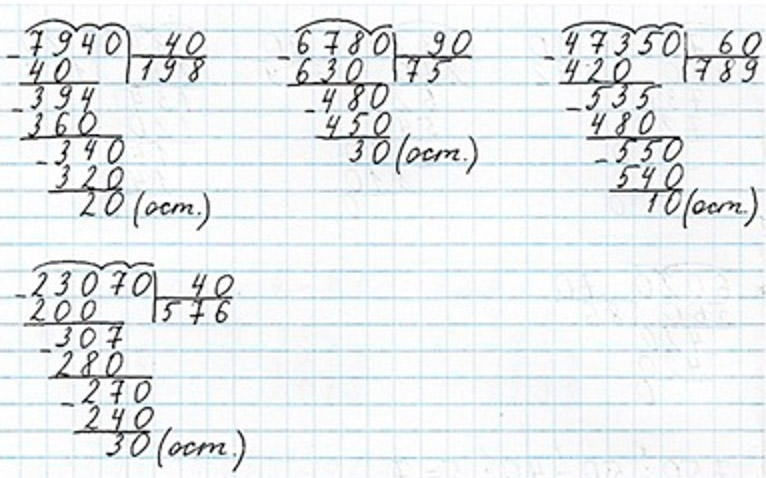
Номер 112.
На завод отправлено 3600 т угля в вагонах, по 60 т в каждом, и столько же угля в вагонах, по 90 т в каждом. Каких вагонов потребовалось больше и на сколько больше?
Ответ:
1) 3600 : 60 = 60 (в.) – угля, было по 60 т.
2) 3600 : 90 = 40 (в.) – угля, было по 90 т.
3) 60 − 40 = 20 (в.) - больше потребовалось вместимостью 60 тонн.
Ответ: на 20 штук потребовалось больше вагонов вместимостью 60 тонн.
Масса – величина предмета, которая может выражаться в граммах, килограммах, центнерах и тонных.
Помним о соотношении числовых значений единиц измерения массы:
1 кг = 1000 г
1 ц = 100 кг
1 т = 1000 кг
Оформляем условие в виде таблицы.

Рассуждаем.
Узнаем, сколько вагонов по 60 тонн перевозили уголь. Для этого количество угля в этих вагонах разделим на количество угля в одном таком вагоне.
1) 3600 : 60 = 60 (в.) – угля, было по 60 т.
Продолжаем рассуждение.
Узнаем, сколько вагонов по 90 тонн перевозили уголь. Для этого количество угля в этих вагонах разделим на количество угля в одном таком вагоне.
2) 3600 : 90 = 40 (в.) – угля, было по 90 т.
Продолжаем рассуждение.
Чтобы узнать, каких вагонов больше перевозили уголь и на сколько, нужно из большего количества вагонов вычесть меньшее.
3) 60 − 40 = 20 (в.)
Записываем ответ.
Ответ: на 20 штук потребовалось больше вагонов вместимостью 60 тонн.
Номер 113.
За 8 мин самолёт, двигаясь с одинаковой скоростью, пролетел 96 км. Какое расстояние он пролетит за 40 мин, если его скорость увеличится на 2 км/мин?
Ответ:
1) 96 : 8 = 12 (км/мин) – была скорость самолёта.
2) 12 + 2 = 14 (км/мин) – увеличенная скорость самолёта.
3) 14 ∙ 40 = 560 (км) - всего пролетит самолёт за 40 минут
Ответ: 560 км пролетит самолёт за 40 мин.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде таблицы.

Рассуждаем.
Найдем скорость самолета, для этого расстояние, которое пролетел самолет разделим на время в пути.
1) 96 : 8 = 12 (км/мин) – была скорость самолета.
Продолжаем рассуждение.
Найдем скорость самолета, после ее увеличения.
2) 12 + 2 = 14 (км/мин) – увеличенная скорость самолета.
Продолжаем рассуждение.
Чтобы узнать расстояние, которое пролетел самолет после увеличения скорости, нужно увеличенную скорость самолета умножить на время в пути.
3) 14 ∙ 40 = 560 (км)
Записываем ответ.
Ответ: 560 км пролетит самолёт за 40 мин.
Задание внизу страницы
Выполни деление с остатком и сделай проверку.
Ответ:
Алгоритм письменного деления на числа, оканчивающиеся нулями:
1. Выделить первое неполное делимое.
2. Определить количество цифр в частном.
3. Разделить неполное делимое на делитель.
4. Умножить делитель на полученное число.
5. Найти остаток от деления вычитанием.
6. Сравнить остаток с делителем.
Вспомним как выполняется проверка.
Проверка:
1) Остаток должен быть меньше делителя.
2) Умножим частное на делитель.
3) Прибавим к результату остаток. Сумма должна быть равна делимому.
Выполняем вычисление и оформляем задание в тетрадь.

Задание на полях страницы
Начерти узор
Ответ:
Рассмотри, из каких фигур состоит узор, какими цветами он раскрашен.
Рассмотрим узор и посчитаем количество клеток.
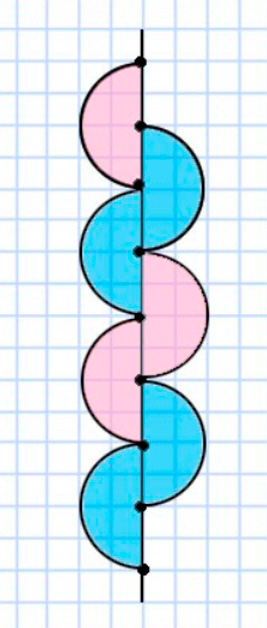
Оформим задание в тетрадь.

Номер 100.
Из 2 м полотна получается 3 наволочки. Сколько таких наволочек получится из 42 м полотна?

2 м – 3 н.
42 м – ? н.
1) 42 : 2 = 21 (раз) – вмещается по 2 м в 42 м.
2) 21 ∙ 3 = 63 (н.) - всего получится из 42 м полотна
Ответ: 63 наволочки всего получится из 42 м полотна.
Вспомни внетабличное умножение и деление.
Оформляем краткую запись.
2 м полотна – 3 наволочки
42 м полотна – ? наволочек
Рассуждаем.
Узнаем, сколько раз по 2 метра вмещается в 42 метра. Для этого разделим 42 метра на 2 метра.
42 : 2 = 21 (раз) – вмещается по 2 м в 42 м.
Продолжаем рассуждение.
Чтобы узнать, сколько наволочек получится из 42 метров полотна, нужно количество наволочек в 2 м умножить на количество раз, сколько эти 2 м вмещаются в 42 м.
3 ∙ 21 = 63 (н.) – получится из 42 м.
Записываем ответ.
Ответ: 63 наволочки получится из 42 м полотна.
Номер 101.
В 10 одинаковых банках 16 кг мёда. Сколько килограммов мёда в 20 таких банках?
Ответ:
10 б. – 16 кг
20 б. – ? кг
1) 20 : 10 = 2 (раза) – во столько раз банок взяли больше.
2) 16 ∙ 2 = 32 (кг) - мёда всего в 20 банках.
Ответ: 32 кг мёда в 20 банках.
Вспомни внетабличное умножение и деление.
Оформляем краткую запись.
10 банок – 16 кг мёда
20 банок – ? кг мёда
Рассуждаем.
Узнаем, во сколько раз банок взяли больше.
20 : 10 = 2 (раза) – во столько раз банок взяли больше.
Продолжаем рассуждение.
Узнаем, сколько кг мёда в 20 банках, для этого количество мёда в 10 банках умножим на 2.
16 ∙ 2 = 32 (кг) – мёда в 20 банках.
Записываем ответ.
Ответ: 32 кг мёда в 20 банках.
Номер 102.
Из двух городов выехали одновременно навстречу друг другу два мотоциклиста. Один из них двигался со скоростью 70 км/ч и проехал до встречи 140 км, а другой двигался со скоростью 65 км/ч. Найди расстояние между городами. Составь и реши задачи, обратные данной.
Ответ:
1) 140 : 70 = 2 (ч) – в пути.
2) 65 ∙ 2 = 130 (км) – проехал второй мотоциклист.
3)140 + 130 = 270 (км) – расстояние между городами.
Ответ: общее расстояние между городами составляет 270 км.
Обратная задача 1:
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоцикла. Один из них двигался со скоростью 70 км/ч, и проехал 140 км. С какой скоростью двигался второй мотоциклист?
1) 140 : 70 = 2 (ч) – время движения.
2) 270 − 140 = 130 (км) – проехал 2-ой мотоциклист.
3) 130 : 2 = 65 (км/ч) – скорость 2-ого мотоциклиста.
Ответ: скорость второго мотоциклиста составляет 65 км/ч.
Обратная задача 2:
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоцикла. Один из них двигался со скоростью 65 км/ч, и проехал 130 км. С какой скоростью двигался второй мотоциклист?
1) 130 : 65 = 2 (ч) – время движения.
2) 270 − 130 = 140 (км) – проехал 2-ой мотоциклист.
3) 140 : 2 = 70 (км/ч) – скорость 2-ого мотоциклиста.
Ответ: скорость второго мотоциклиста составляет 70 км/ч.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Оформляем условие в виде схематического чертежа.
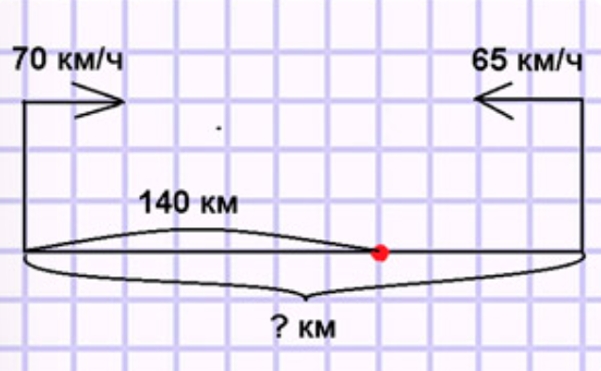
Рассуждаем.
Узнаем, какое время мотоциклисты были в пути. Для этого расстояние, которое проехал первый мотоциклист разделим на его скорость.
140 : 70 = 2 (ч) – были в пути мотоциклисты.
Продолжаем рассуждение.
Зная время, мы можем узнать расстояние, которое проехал второй мотоциклист. Для этого скорость второго мотоциклиста умножаем на время.
65 ∙ 2 = 130 (км) – проехал второй мотоциклист.
Продолжаем рассуждение.
Чтобы узнать расстояние между городами, нужно сложить вместе расстояния, которые проехали оба мотоциклиста до встречи друг с другом.
140 + 130 = 270 (км) – расстояние между городами.
Записываем ответ.
Ответ: расстояние между городами составляет 270 км.
Шаг 1.
Составляем задачу.
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоциклиста. Один из них двигался со скоростью 70 км/ч и проехал 140 км. С какой скоростью двигался второй мотоциклист?
Рассуждаем.
Узнаем, какое время мотоциклисты были в пути. Для этого расстояние, которое проехал первый мотоциклист разделим на его скорость.
140 : 70 = 2 (ч) – были в пути мотоциклисты.
Продолжаем рассуждение.
Чтобы узнать, какое расстояние проехал второй мотоциклист, нужно из общего расстояния между городами вычесть расстояние, которое проехал первый мотоциклист.
270 – 140 = 130 (км) – проехал второй мотоциклист.
Продолжаем рассуждение.
Зная время, мы можем узнать скорость, с которой ехал второй мотоциклист. Для этого расстояние, которое проехал второй мотоциклист, разделим на время.
130 : 2 = 65 (км/ч) – скорость второго мотоциклиста.
Записываем ответ.
Ответ: скорость второго мотоциклиста составляет 65 км/ч.
Шаг 1.
Составляем задачу.
Из двух городов, расстояние между которыми 270 км, выехали одновременно навстречу друг другу два мотоциклиста. Второй мотоциклист ехал со скоростью 65 км/ч и проехал 130 км. С какой скоростью двигался первый мотоциклист?
Рассуждаем.
Узнаем, какое время мотоциклисты были в пути. Для этого расстояние, которое проехал второй мотоциклист разделим на его скорость.
130 : 65 = 2 (ч) – были в пути мотоциклисты.
Продолжаем рассуждение.
Чтобы узнать, какое расстояние проехал первый мотоциклист, нужно из общего расстояния между городами вычесть расстояние, которое проехал второй мотоциклист.
270 – 130 = 140 (км) – проехал первый мотоциклист.
Продолжаем рассуждение.
Чтобы узнать скорость первого мотоциклиста, нужно расстояние, которое он проехал, разделить на время.
140 : 2 = 70 (км/ч) – скорость первого мотоциклиста.
Записываем ответ.
Ответ: скорость первого мотоциклиста составляет 70 км/ч.
Номер 103.
Запиши равенства и неравенства, проверь, верны ли они.
1) Произведение чисел 293 и 70 равно разности чисел 2900 и 849.
2) Сумма чисел 9391 и 7028 равна частному чисел 82095 и 5.
3) Частное чисел 70236 и 9 меньше их разности.
4) Произведение чисел 8019 и 7 больше их суммы.
1) 293 ∙ 70 = 2900 − 849 – неверно 2) 9391 + 7028 = 82095 : 5 – верно 3) 70236 : 9 < 70236 − 9 – верно 4) 8019 ∙ 7 > 8019 + 7 – верно


«>» – знак «больше»
«<» – знак «меньше»
«=» – знак «равно»
Рассуждаем.
1) 293 ∙ 70 = 2900 − 849
Проверим верно ли это равенство.
Для этого вычислим выражения.
293 ∙ 70 = 20510
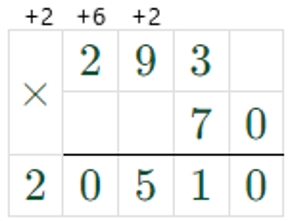
2900 – 849 = 2051
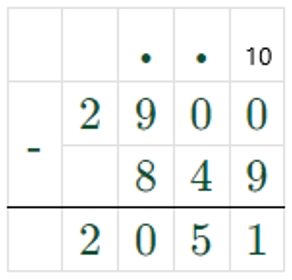
20510 ≠ 2051, значит
293 ∙ 70 = 2900 – 849 – неверно
2) 9391 + 7028 = 82095 : 5
Проверим верно ли это равенство.
Для этого вычислим выражения.
9391 + 7028 = 16419
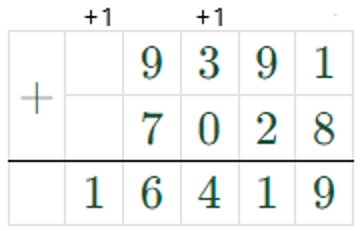
82095 : 5 = 16419
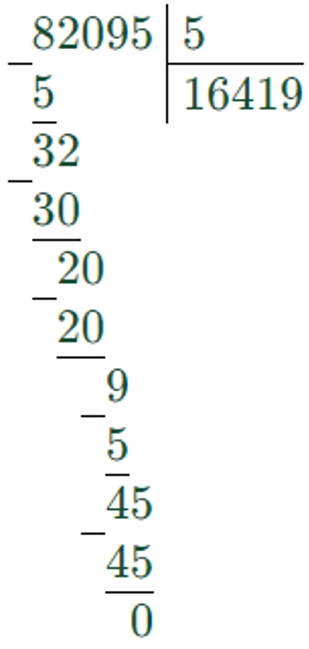
16419 = 16419, значит
9391 + 7028 = 82095 : 5 – верно
3) 70236 : 9 < 70236 − 9
Проверим верно ли это неравенство.
Для этого вычислим выражения.
70236 : 9 = 7804
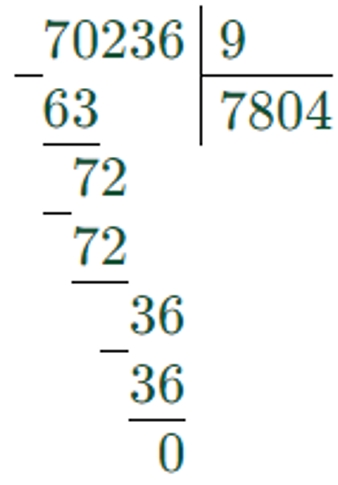
70236 – 9 = 70227
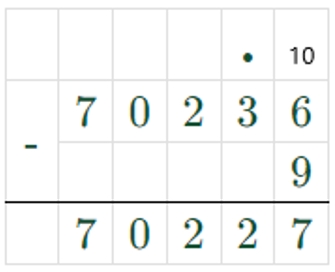
7804 < 70227, значит
70236 : 9 < 70236 − 9 – верно
4) 8019 ∙ 7 > 8019 + 7
Проверим верно ли это неравенство.
Для этого вычислим выражения.
8019 ∙ 7 = 56133
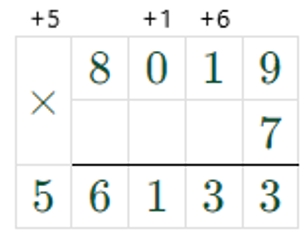
8019 + 7 = 8026
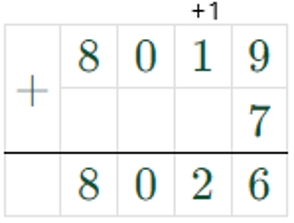
56133 > 8026, значит
8019 ∙ 7 > 8019 + 7 – верно
Запишем ответ.
1) 293 ∙ 70 = 2900 − 849 – неверно
2) 9391 + 7028 = 82095 : 5 – верно
3) 70236 : 9 < 70236 − 9 – верно
4) 8019 ∙ 7 > 8019 + 7 – верно
Номер 104.
Выполни деление с остатком и проверь решение.
Ответ:1724 : 10 = 172 (ост.4) Проверка: 1) 4 < 10 2) 172 ∙ 10 + 4 = 1724 1720 2540 : 100 = 25 (ост.40) Проверка: 1) 40 < 100 2) 25 ∙ 100 + 40 = 2540 2500 65032 : 1000 = 65 (ост.32) Проверка: 1) 32 < 1000 2) 65 ∙ 1000 + 32 = 65032 65000
1) Вспомни, как выполнять деление с остатком и делать проверку.
2) Вспомни, как делить на 10, на 100 и на 1000.
Вычисляем.
1724 : 10 = 172 (ост. 4)
Без остатка 1724 на 10 не разделится.
1720 : 10 = 172 – частное
1724 – 1720 = 4 – остаток
Проверка:
1) 4 < 10
2) 172 ∙ 10 + 4 = 1724
2540 : 100 = 25 (ост. 40)
Без остатка 2540 на 100 не разделится.
2500 : 100 = 25 – частное
2540 – 2500 = 40 – остаток
Проверка:
1) 40 < 100
2) 25 ∙ 100 + 40 = 2540
65032 : 1000 = 65 (ост. 32)
Без остатка 65032 на 1000 не разделится.
65000 : 1000 = 65 – частное
65032 – 65000 = 32 – остаток
Проверка:
1) 32 < 1000
2) 65 ∙ 1000 + 32 = 65032
Оформим задание в тетрадь.
1724 : 10 = 172 (ост. 4)
Проверка:
1) 4 < 10
2) 172 ∙ 10 + 4 = 1724
2540 : 100 = 25 (ост. 40)
Проверка:
1) 40 < 100
2) 25 ∙ 100 + 40 = 2540
65032 : 1000 = 65 (ост. 32)
Проверка:
1) 32 < 1000
2) 65 ∙ 1000 + 32 = 65032
Номер 105.
Ответ:


1) Помни, как разделить число на произведение.
2) Помни, как разделить число на 10 и на 100.
Вычисляем.
140 : 20 = 140 : (10 ∙ 2) = 140 : 10 : 2 = 14 : 2 = 7
Представим делитель 20 в виде произведения чисел 10 и 2, разделим число 140 на первый множитель – 10, затем полученный результат разделим на второй множитель – 2.
560 : 7 = 56 дес. : 7 = 8 дес. = 80
10 = 1 дес.
8100 : 900 = 8100 : (100 ∙ 9) = 8100 : 100 : 9 = 81 : 9 = 9
Представим делитель 900 в виде произведения чисел 100 и 9, разделим число 8100 на первый множитель – 100, затем полученный результат разделим на второй множитель – 9.
3200 : 800 = 3200 : (100 ∙ 8) = 3200 : 100 : 8 = 32 : 8 = 4
Представим делитель 800 в виде произведения чисел 100 и 8, разделим число 3200 на первый множитель – 100, затем полученный результат разделим на второй множитель – 8.
500 + (600 – 3 ∙ 100) : 10 = 500 + (600 – 300) : 10 = 500 + 300 : 10 = 500 + 30 = 530
Сначала выполняются действия в скобках – умножение, затем сложение. После этого действия вне скобок – деление, затем вычитание.
9000 : (100 – 90) : 9 ∙ 2 = 9000 : 10 : 9 ∙ 2 = 900 : 9 ∙ 2 = 100 ∙ 2 = 200
Сначала выполняется действие в скобках – вычитание, затем действия вне скобок по порядку слева направо.
Оформим задание в тетрадь.
140 : 20 = 140 : (10 ∙ 2) = 140 : 10 : 2 = 14 : 2 = 7
560 : 7 = 56 дес. : 7 = 8 дес. = 80
8100 : 900 = 8100 : (100 ∙ 9) = 8100 : 100 : 9 = 81 : 9 = 9
3200 : 800 = 3200 : (100 ∙ 8) = 3200 : 100 : 8 = 32 : 8 = 4
500 + (600 – 3 ∙ 100) : 10 = 500 + (600 – 300) : 10 = 500 + 300 : 10 = 500 + 30 = 530
9000 : (100 – 90) : 9 ∙ 2 = 9000 : 10 : 9 ∙ 2 = 900 : 9 ∙ 2 = 100 ∙ 2 = 200
Номер 106.
У моей мамы рост 164 см. Мой брат на 16 см выше мамы, а я пока на 8 см ниже мамы. Какой у меня рост? Сделай схематический чертёж к задаче и определи, на сколько сантиметров брат выше меня.
Ответ:
1) 164 + 16 = 180 (см) – рост брата.
2) 164 − 8 = 156 (см) – мой рост.
3) 180 − 156 = 24 (см) – разница.
Задачу проще решить, сделав схематический чертёж:

8 + 16 = 24 (см) - всего брат выше меня
Ответ: на 24 см брат выше меня.
Чтобы узнать, насколько одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
Оформляем краткую запись.
Рассуждаем.
Чтобы узнать рост брата, нужно к росту мамы прибавить 16 см, потому что брат выше мамы на 16 см.
164 + 16 = 180 (см) – рост брата.
Продолжаем рассуждение.
Узнаем, какой рост у меня. Для этого из роста мамы вычтем 8 см, потому что известно, что я ниже мамы на 8 см.
164 – 8 = 156 (см) – мой рост.
Продолжаем рассуждение.
Теперь узнаем, на сколько сантиметров мой брат выше меня, для этого нужно из роста брата вычесть мой рост.
180 – 156 = 24 (см) – на столько брат выше меня.
Продолжаем рассуждение.
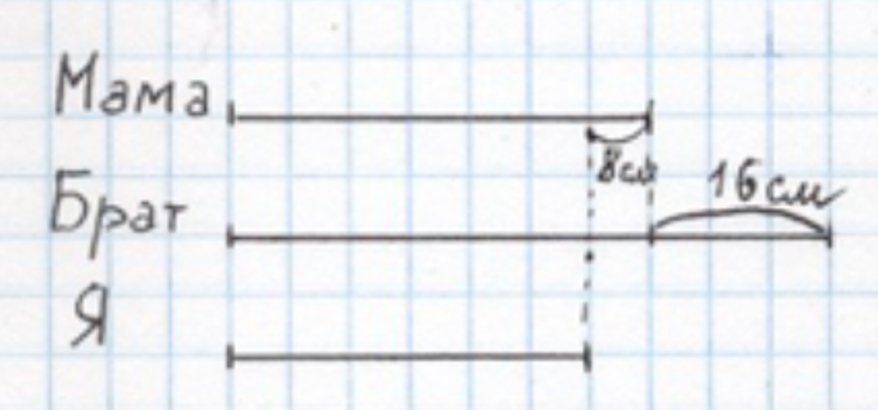
Если сделать схематический чертёж, то, чтобы найти разницу в росте у нас с братом, достаточно сложить нашу разницу в росте с мамой.
8 + 16 = 24 (см) – разница в росте.
Записываем ответ.
Ответ: мой рост – 156 см, брат выше на 24 см.
Задание внизу страницы
Сумма трёх чисел 2010. Первое слагаемое 980, оно в 2 раза больше второго. Найди третье слагаемое.
Ответ:
1) 980 : 2 = 490 – слагаемое.
2) 980 + 490 = 1470 – сумма 1 и 2 слагаемых.
3) 2010 – 1470 = 540 – третье слагаемое.
Выражение:
2010 − (980 + 980 : 2) = 540
Ответ: 540 третье слагаемое.
Оформляем условие задачи в виде краткой записи.
Оформляем краткую запись.
1 слагаемое – 980
2 слагаемое – ? в 2 раза меньше первого
3 слагаемое – ?
Сумма – 2010
Рассуждаем.
Найдем второе слагаемое, для этого значение первого слагаемого разделим на 2, так как известно, что второе слагаемое в два раза меньше, чем первое.
980 : 2 = (800 + 180) : 2 = 400 + 90 = 490 – второе слагаемое.
Продолжаем рассуждение.
Узнаем сумму 1-го и 2-го слагаемых, для этого сложим их значения.
980 + 490 = 900 + 80 + 400 + 90 = 1300 + 170 = 1470 – сумма 1 и 2 слагаемых.
Продолжаем рассуждение.
Чтобы узнать значение третьего слагаемого, нужно из суммы всех значений вычесть сумму 1 и 2 слагаемых.
2010 – 1470 = 540 – третье слагаемое.
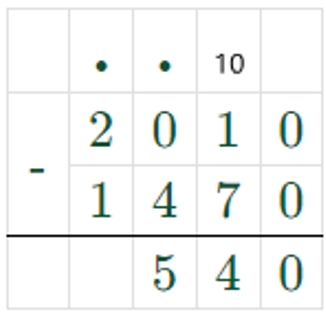
Записываем ответ.
Ответ: 540 третье слагаемое.
Решение выражением: 2010 − (980 + 980 : 2) = 540
Задание на полях страницы


Вместо фигур нужно вставить числа, чтобы равенства стали верными.
Рассмотрим рисунок.
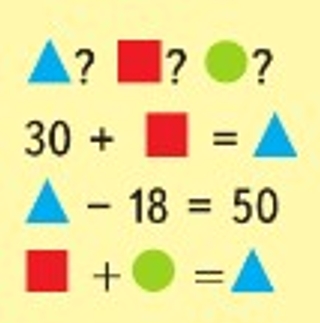
Рассуждаем.
Рассмотрим второе выражение.
△ – 18 = 50
Неизвестно уменьшаемое.
Чтобы найти уменьшаемое, нужно к сумме прибавить вычитаемое.
50 + 18 = 68
Значит, число за синим треугольником – это число 68.
Продолжаем рассуждение.
Рассмотрим первое выражение.
Во первом примере заменим треугольник на число 68, получим:
30 + ☐ = 68
Неизвестно слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
68 – 30 = 38
Значит, число за красным квадратом – это число 38.
Продолжаем рассуждение.
Рассмотрим третье выражение.
В третьем примере заменим треугольник на число 68, а квадрат – на число 38, получим:
38 + ◯ = 68
Неизвестно слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
68 – 38 = 30
Значит, число за зеленым кругом – это число 30.
Делаем проверку.
30 + 38 = (30 + 30) + 8 = 60 + 8 = 68
68 – 18 = 60 + 8 – 10 – 8 = 60 – 10 = 50
38 + 30 = (30 + 30) + 8 = 60 + 8 = 68
Оформляем задание в тетрадь.
Треугольник = 68
Квадрат = 38
Круг = 30
Проверка:

С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.