Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 23

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 29.
Сравни:
1) сумму чисел 5237 и 786 с числом 6000; 2) число 800 с разностью чисел 1560 и 760; 3) произведение чисел 384 и 200 с числом 7800; 4) число 460 с частным от деления чисел 3000 и 6.
Ответ:1) 5237 + 786 > 6000 6023 > 6000

2) 1560 − 760 = 800 800 = 800

3) 384 ∙ 200 > 7800 76800 > 7800

4) 3000 : 6 > 460 500 > 460
«>» – знак «больше»
«<» – знак «меньше»
«=» – знак «равно»
Сравним сумму чисел 5237 и 786 с числом 6000.
1) 5237 + 786 > 6000
6023 > 6000
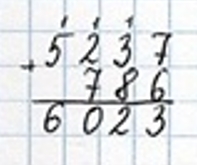
Сравним число 800 с разностью чисел 1560 и 760.
2) 1560 − 760 = 800
800 = 800
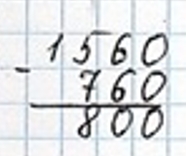
Сравним произведение чисел 384 и 200 с числом 7800.
3) 384 ∙ 200 > 7800
76800 > 7800
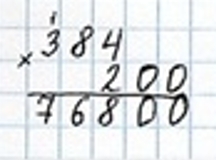
Сравним число 460 с частным от деления чисел 3000 и 6.
4) 3000 : 6 > 460
500 > 460
Номер 30.
Вспомни виды треугольников (с. 126).
1) Найди суммы чисел, записанных в остроугольных треугольниках.
2) Из чисел, записанных в прямоугольных треугольниках, составь разности, которые ты можешь вычислить. Умножь каждый из полученных результатов на число, записанное в тупоугольном треугольнике.

Остроугольные треугольники: 739 и 60.
Прямоугольные треугольники: 400, 675, 928, 586.
Тупоугольные треугольники: 100.
1) 739 + 60 = 799
2) 675 − 400 = 275
675 − 586 = 89
275 ∙ 100 = 27500
89 ∙ 100 = 8900
586 − 400 = 186
928 − 675 = 253
186 ∙ 100 = 18600
253 ∙ 100 = 25300
928 − 400 = 528
928 − 586 = 342
528 ∙ 100 = 52800
342 ∙ 100 = 34200
Виды треугольников
1) По видам углов треугольники различаются так:
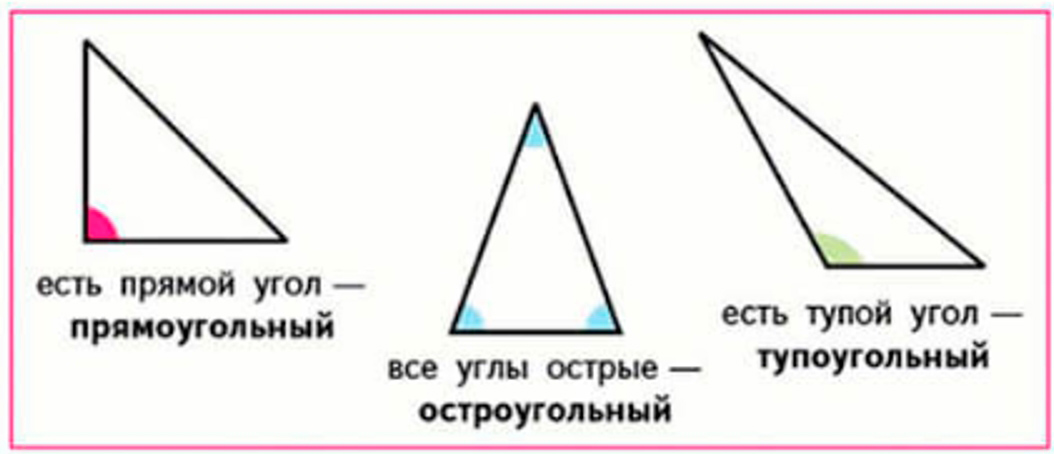
2) Треугольники различаются по тому, равны ли длины сторон:
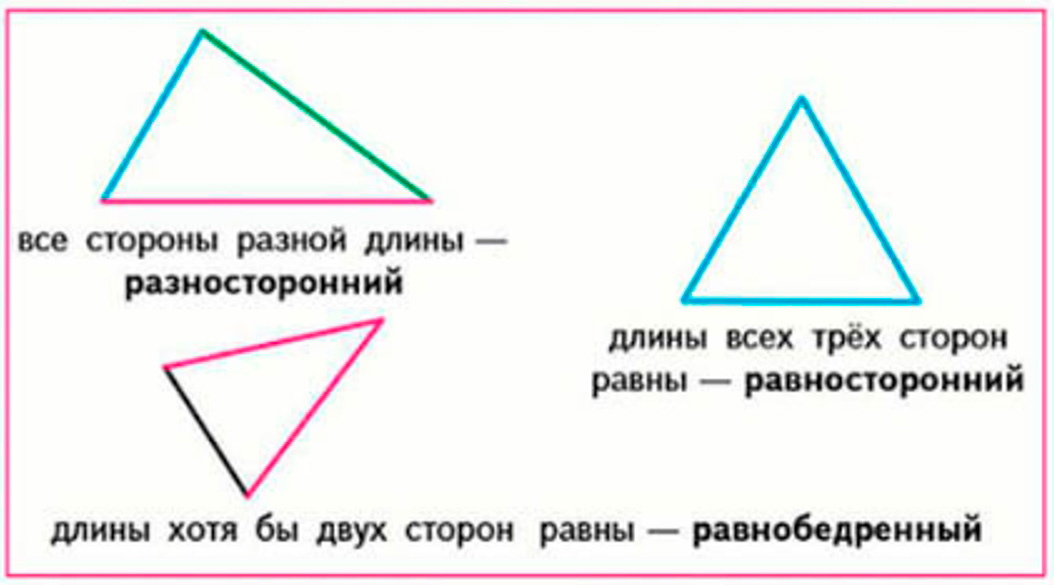
Внимательно рассмотрим треугольники, данные в задании, и охарактеризуем их.
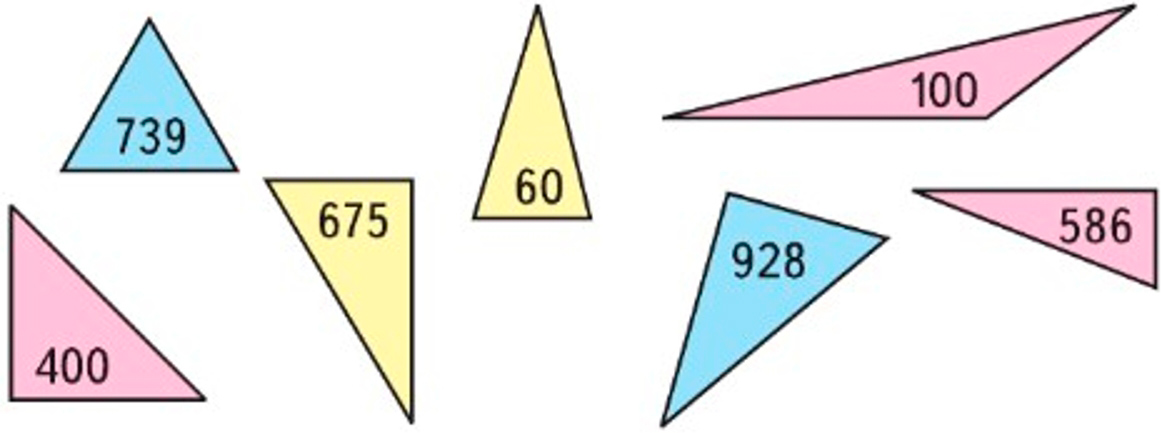
Остроугольные треугольники: 739 и 60.
Прямоугольные треугольники: 400, 675, 928, 586.
Тупоугольные треугольники: 100.
Найдем суммы чисел, записанных в остроугольных треугольниках.
739 + 60 = 799
Выполним вычисления по данным в задании.
675 – 400 = 275
675 – 586 = 89
275 ∙ 100 = 27500
89 ∙ 100 = 8900
586 – 400 = 186
928 – 675 = 253
186 ∙ 100 = 18600
253 ∙ 100 = 25300
928 – 400 = 528
928 – 586 = 342
528 ∙ 100 = 52800
342 ∙ 100 = 34200
Номер 31.
На книжной выставке представлены 1370 книг. Из них учебников для младших школьников – 156, это в 3 раза меньше, чем учебников для старших школьников, а учебников для студентов столько, сколько учебников для младших и старших школьников вместе. Остальные книги – для учителей. Сколько книг для учителей представлено на выставке?
Ответ:
1) 156 ∙ 3 = 468 (кн.) - для старших школьников.
2) 156 + 468 = 624 (кн.) - для студентов.
3) 156 + 468 + 624 = 1248 (кн.) - всего.
4) 1370 − 1248 = 122 (кн.) - для учителей.
Ответ: 122 книги для учителей всего представлено на выставке.
Оформляем условие задачи в виде краткой записи.
Оформляем условие.

Рассуждаем.
Узнаем сколько учебников для старших школьников. Для этого количество учебников для младших школьников умножим на 3, так как известно, что книг для старших школьников в три раза больше.
1) 156 ∙ 3 = 468 (кн.) – для старших школьников.
Продолжаем рассуждение .
Узнаем сколько учебников для студентов. Для этого сложим количество учебников для младших и для старших школьников.
2) 156 + 468 = 624 (кн.) – для студентов.
Продолжаем рассуждение.
Теперь мы можем узнать, сколько учебников всего для учащихся.
3) 156 + 468 + 624 = 1248 (кн.) – всего.
Продолжаем рассуждение.
Чтобы узнать, сколько книг для учителей, нужно из общего количества книг вычесть количество книг для учащихся.
4) 1370 − 1248 = 122 (кн.) – для учителей.
Записываем ответ.
Ответ: 122 книги.
Номер 32.
Вычислительная машина работает так:

Какое число будет получаться на выходе из машины, если на входе будет число: 5; 7; 11; 9; 12?
Ответ:5 ∙ 300 – 1 = 1500 – 1 = 1499; 7 ∙ 300 – 1 = 2100 – 1 = 2099; 11 ∙ 300 – 1 = 3300 – 1 = 3299; 9 ∙ 300 – 1 = 2700 – 1 = 2699; 12 ∙ 300 – 1 = 3600 – 1 = 3599.
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассмотрим как работает вычислительная машина.
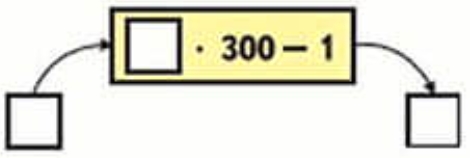
Выполним вычисления с данными числами.
5 ∙ 300 – 1 = 1500 – 1 = 1499;
7 ∙ 300 – 1 = 2100 – 1 = 2099;
11 ∙ 300 – 1 = 3300 – 1 = 3299;
9 ∙ 300 – 1 = 2700 – 1 = 2699;
12 ∙ 300 – 1 = 3600 – 1 = 3599.
Номер 1.
Какие свойства умножения ты знаешь? (с. 120.)
Ответ:Я знаю такие свойства умножения: 1. При перестановке множителей произведение не меняется. 2. При умножении числа на произведение можно это число умножить на одно из двух чисел произведения и записать это действие в скобках, а затем новое произведение умножить на оставшееся число. 3. При умножении суммы на число, можно отдельно умножить на число каждое слагаемое, а результаты сложить.
Чтобы ответить на вопросы обратись к странице 120 учебника.
Перечислим известные нам свойства умножения.
1. При перестановке множителей произведение не меняется.
2. При умножении числа на произведение можно это число умножить на одно из двух чисел произведения и записать это действие в скобках, а затем новое произведение умножить на оставшееся число.
3. При умножении суммы на число, можно отдельно умножить на число каждое слагаемое, а результаты сложить.
Оформим задание.
Номер 2.
Объясни на примере, как можно умножить число на произведение.
Ответ:Например, 6 ∙ (2 ∙ 5) = (6 ∙ 2) ∙ 5, при этом значение выражения не меняется. 6 ∙ (2 ∙ 5) = 60 и (6 ∙ 2) ∙ 5 = 60
Чтобы ответить на вопросы обратись к странице 120 учебника.
Приведем пример вычислений по данным из задания.
Например:
• 6 ∙ (2 ∙ 5) = (6 ∙ 2) ∙ 5, при этом значение выражения не меняется.
• 6 ∙ (2 ∙ 5) = 60
• (6 ∙ 2) ∙ 5 = 60
Оформим задание.
Задание на полях страницы
Продолжи 111 : 3, 222 : 3, 333 : 3, 444 : 3, ...
Ответ:555 : 3, 666 : 3, 777 : 3, 888 : 3 , 999 : 3.
Внимательно рассмотри примеры и найди закономерность построения ряда.
Продолжим ряд 111 : 3, 222 : 3, 333 : 3, 444 : 3, ...
555 : 3
666 : 3
777 : 3
888 : 3
999 : 3
Оформим задание в тетрадь.
Номер 10.
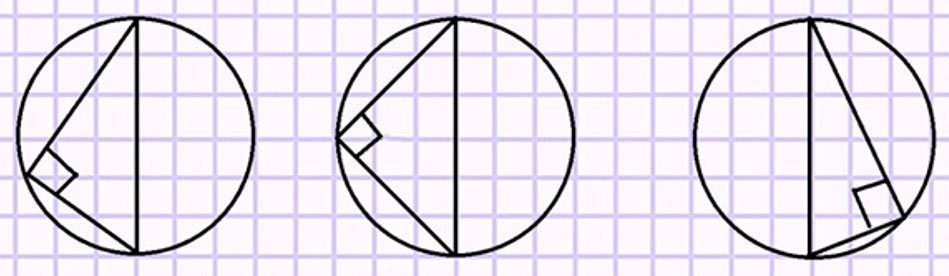
Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Какого вида треугольник начертили? Подтверди свой ответ.
Ответ:
Получился прямоугольный треугольник.
1) Вспомни виды треугольников.
2) Диаметр – это прямая, проходящая через центр окружности и соединяющая две точки на окружности.
Начертим окружность.
Чтобы начертить окружность, воспользуемся циркулем.
Возьмём радиус 1,5 см, зафиксируем центр окружности и начертим окружность.
Проведём диаметр.
Соединим концы диаметра с произвольной точкой на окружности.
Получился прямоугольный треугольник, так как один из его углов равен 90°.
Делаем вывод.
Какую бы точку на окружности мы не отметили, если её соединить с концами диаметра, то в результате получается прямоугольный треугольник.
Оформим задание в тетрадь.
Номер 11.
Вычисли значение выражения а : b, если: 1) а = 7020 и b = 6; 2) а = 17418 и b = 3.
Ответ:
Вспомни, как делить многозначные числа столбиком.
Выполняем вычисления.
Если а = 7020 и b = 6, то
a : b = 7020 : 6 = 1170
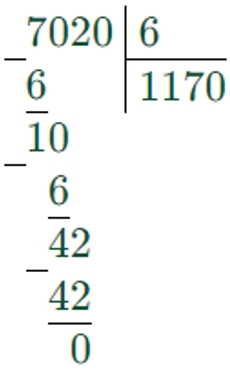
Делим по разрядам, слева направо.
Делим тысячи:
7 : 6 = 1 (ост. 1)
В частное пишем 1 тыс., а остаток уходит в сотни.
Делим сотни:
В остатке осталась 1 тыс. = 10 сот.
В делимом в разряде сотни 0, получаем 10 + 0 = 10
10 : 6 = 1 (ост. 4)
В частное пишем 1 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 4 сот. = 40 дес.
В делимом в разряде десятков 2, получаем 40 + 2 = 42
42 : 6 = 7
В частном пишем 7 дес.
Делим единицы:
0 : 6 = 0
В частном пишем 0 ед.
Если а = 17418 и b = 3
a : b = 17418 : 3 = 5806
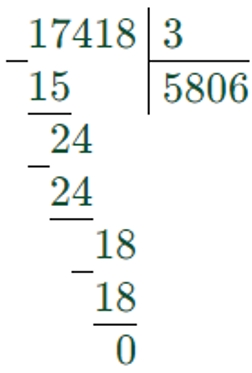
Делим по разрядам, слева направо.
Делим десятки тысяч:
1 : 3 = 0 (ост. 1)
В ответ ничего не пишем, а остаток уходит в тысячи.
Делим тысячи:
В остатке 1 дес.тыс. = 10 тыс.
В делимом в разряде тысячи 7, получаем 10 + 7 = 17
17 : 3 = 5 (ост. 2)
В частное пишем 5 тыс., а остаток уходит в сотни.
Делим сотни:
В остатке 2 тыс. = 20 сот.
В делимом в разряде сотни 4, получаем 20 + 4 = 24
24 : 3 = 8
В частное пишем 8 сот.
Делим десятки:
1 : 3 = 0 (ост. 1)
В частном пишем 0 дес., а остаток уходит в единицы.
Делим единицы:
В остатке 1 дес. = 10 ед.
В делимом в разряде единицы 8, получаем 10 + 8 = 18
18 : 3 = 6
В частное пишем 6 ед.
Оформим задание в тетрадь.
1) 7020 : 6 = 1170
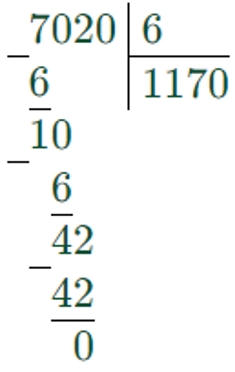
2) 17418 : 3 = 5806
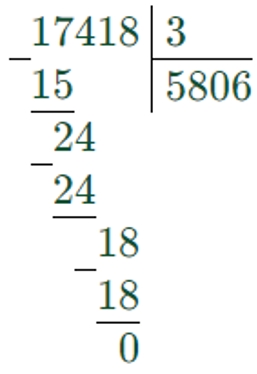
Номер 12.
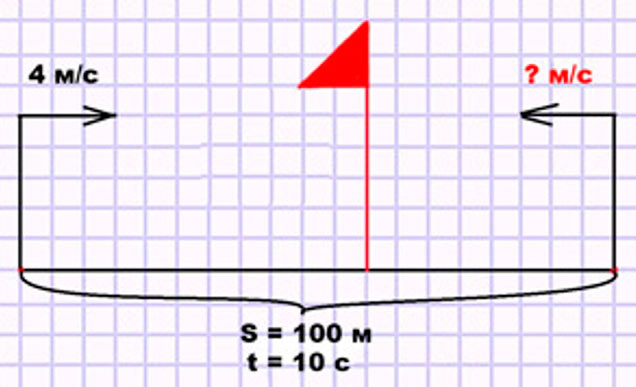
Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скоростью 4 м/с. С какой скоростью бежал второй мальчик?
Ответ:
1) 4 ∙ 10 = 40 (м) – пробежал первый мальчик.
2) 100 − 40 = 60 (м) – пробежал второй мальчик.
3) 60 : 10 = 6 (м/с) - скорость второго мальчика.
Ответ: 6 м/с скорость второго мальчика.
1) 100 : 10 = 10 (м/с) – скорость сближения.
2) 10 – 4 = 6 (м/с)
Ответ: 6 м/с скорость второго мальчика.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
Шаг 1.
Рассуждаем.
Узнаем, сколько метров пробежал первый мальчик, для этого скорость умножим на время.
4 ∙ 10 = 40 (м) – пробежал первый мальчик.
Продолжаем рассуждение.
Чтобы узнать, сколько метров пробежал второй мальчик, нужно из длины всей дорожки вычесть количество метров, которые пробежал первый мальчик.
100 − 40 = 60 (м) – пробежал второй мальчик.
Продолжаем рассуждение.
Чтобы узнать, с какой скоростью бежал второй мальчик, нужно расстояние, которое он пробежал разделить на время.
60 : 10 = 6 (м/с) – скорость второго мальчика.
Записываем ответ.
Ответ: 6 м/с скорость второго мальчика.
Шаг 1.
Рассуждаем.
Узнаем скорость, с которой мальчики приближались друг к другу, для этого расстояние разделим на время, через которое они встретились.
100 : 10 = 10 (м/с) – скорость сближения.
Продолжаем рассуждение.
Чтобы узнать, с какой скоростью бежал второй мальчик, нужно из общей скорость мальчиков вычесть скорость, с которой бежал первый мальчик.
10 – 4 = 6 (м/с) – скорость второго мальчика.
Записываем ответ.
Ответ: 6 м/с скорость второго мальчика.
Номер 13.
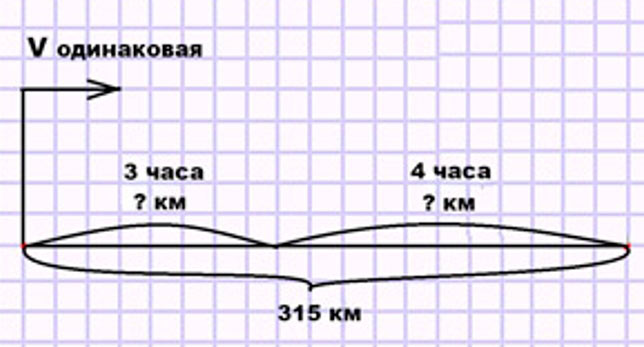
Товарный поезд прошёл 315 км. Он был в пути до остановки 3 ч и после остановки 4 ч. Сколько километров прошёл поезд до остановки и сколько после, если он шёл с одинаковой скоростью?
Ответ:
1) 3 + 4 = 7 (ч) – поезд был в пути.
2) 315 : 7 = 45 (км/ч) – скорость поезда.
3) 45 ∙ 3 = 135 (км) – прошел до остановки.
4) 315 − 135 = 180 (км) – прошел после остановки.
Ответ: 135 км прошёл поезд до остановки всего, 180 км всего шёл поезд до остановки и после.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
Рассуждаем.
Узнаем, сколько часов поезд был в пути. Для этого сложим время в пути до остановки и после.
3 + 4 = 7 (ч) – поезд был в пути.
Продолжаем рассуждение.
Узнаем скорость поезда, для этого расстояние, которое он прошел, разделим на время, которое он был в пути.
315 : 7 = 45 (км/ч) – скорость поезда.
Продолжаем рассуждение.
Теперь узнаем, сколько километров поезд прошел до остановки. Для этого скорость поезда умножим на время, которое он был в пути до остановки.
45 ∙ 3 = 135 (км) – прошел до остановки.
Продолжаем рассуждение.
Чтобы узнать, сколько километров поезд прошел после остановки, нужно из всего расстояния, которое он прошел, вычесть расстояние, которое поезд прошел до остановки.
315 − 135 = 180 (км) – прошел после остановки.
Записываем ответ.
Ответ: 135 км прошёл поезд до остановки, 180 км прошёл поезд после остановки.
Номер 14.
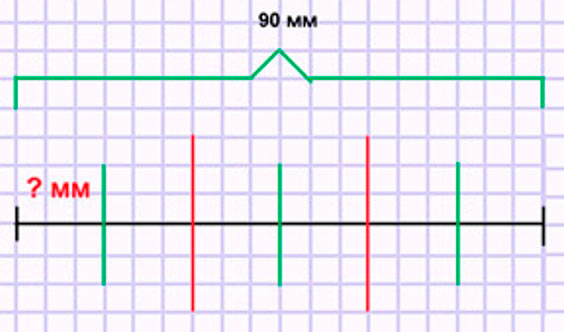
Отрезок длиной 90 мм разделили сначала на 3 равные части, а затем каждую из них разделили на 2 равные части. На сколько равных частей разделили весь отрезок? Чему равна длина одной шестой части данного отрезка? Сделай по задаче чертёж и реши её.
Ответ:
Отрезок разделили на 6 равных частей.
90 : 6 = 15 (мм) – длина одной шестой части данного отрезка.
Ответ:на 6 частей всего разделили отрезок, длина одной шестой части отрезка составляет 15 мм.
Вспомни единицы измерения длины, что 1 см = 10 мм.
Оформляем условие в виде схематического чертежа.
Рассуждаем.
Сначала отрезок разделили на 3 равные части, затем каждую часть ещё раз разделили, но уже на 2 равные части, то есть частей стало в 2 раза больше.
3 ∙ 2 = 6 (ч.) – на столько частей разделили отрезок.
Продолжаем рассуждения.
Чтобы узнать, чему равна одна шестая части отрезка, весь отрезок нужно разделить на 6 равных частей.
90 : 6 = 15 (мм) – длина одной шестой части данного отрезка.
Записываем ответ.
Ответ: 6 равных частей, 15 мм длина одной части отрезка.
Номер 15.
На день работы автобусному парку нужно было 736 л бензина. После установки на автобусы гибридных двигателей расход топлива уменьшился в 4 раза. Сколько литров бензина нужно теперь автобусному парку на 1 день? на 3 дня?
Гибридный двигатель совмещает работу двух двигателей. Один из них работает на бензине, а другой – на электричестве.

1) 736 : 4 = 184 (л) – бензина нужно теперь на 1 день;
2) 184 · 3 = 552 (л) – бензина нужно теперь на 3 дня.
Ответ: 184 л бензина нужно всего на 1 день автобусному парку; 552 л бензина всего нужно на 3 дня автобусному парку.
«В 4 раза меньше» – решается делением.
Оформляем краткую запись.
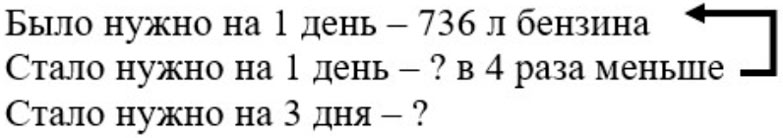
Рассуждаем.
По условию задачи расход топлива уменьшился в 4 раза. Чтобы узнать, сколько литров бензина нужно теперь автобусному парку на 1 день, нужно количество бензина, которое раньше требовалось, разделить на 4.
736 : 4 = 184 (л) – бензина нужно на 1 день.
Продолжаем рассуждение.
Чтобы узнать, сколько литров бензина нужно теперь автобусному парку на 3 день, нужно количество бензина, которое требуется теперь на 1 день, умножить на 3.
184 ∙ 3 = 552 (л) – бензина нужно на 3 дня.
Записываем ответ.
Ответ: 184 л бензина теперь нужно на 1 день, 552 л бензина теперь нужно на 3 дня.
Номер 16.
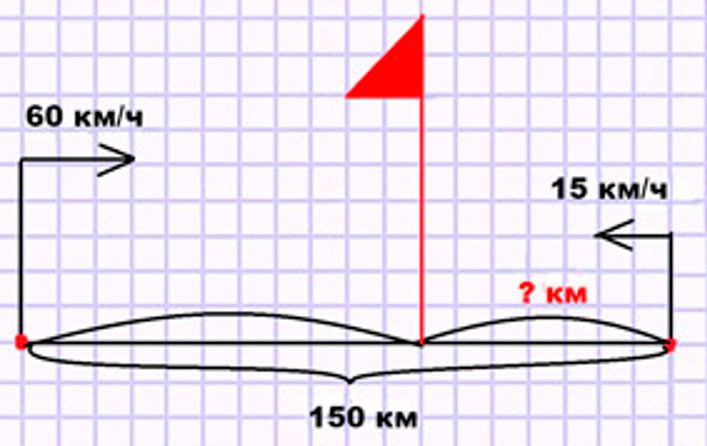
Расстояние между городом и зимовкой 150 км. Из города к зимовке выехали аэросани и двигались со скоростью 60 км/ч. В это же время навстречу им из зимовки по той же дороге пошёл лыжник со скоростью 15 км/ч. На каком расстоянии от зимовки он встретил аэросани?
Ответ:
1) 60 + 15 = 75 (км/ч) – скорость сближения.
2) 150 : 75 = 2 (ч) – время пути.
3) 15 ∙ 2 = 30 (км) – на таком расстоянии от зимовки лыжник встретил аэросани.
Ответ: лыжник встретил аэросани на расстоянии 30 километров от зимовки.
1) Чтобы найти расстояние, надо скорость умножить на время.
2) Чтобы найти скорость, надо расстояние разделить на время.
3) Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
Рассуждаем.
Найдем скорость сближения лыжника с аэросанями. Для этого сложим скорости каждого вместе.
60 + 15 = 75 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Узнаем, какое время они провели в пути до встречи. Для этого расстояние делим на скорость сближения.
150 : 75 = 2 (ч) – время пути.
Продолжаем рассуждение.
Узнаем, на каком расстоянии от зимовки лыжник встретил аэросани. Для этого скорость лыжника умножим на время в пути.
15 ∙ 2 = 30 (км) – на таком расстоянии от зимовки лыжник встретил аэросани.
Записываем ответ.
Ответ: на расстоянии 30 км от зимовки лыжник встретил аэросани.
Номер 17.
Найди ошибки в вычислениях и реши правильно.
Ответ:
1751 : 5 = 350 (ост. 1) решено неверно, так как первое неполное делимое 17, в частном должно быть 3 цифры.
1983 : 9 = 22 (ост. 3) решено неверно, так как первое неполное делимое 19, в частном должно быть 3 цифры.
2930 : 7 = 41 (ост. 6) решено неверно, так как первое неполное делимое 29, в частном должно быть 3 цифры.
40202 : 6 = 670 (ост. 2) решено неверно, так как первое неполное делимое 40, в частном должно быть 4 цифры.
Правильное решение:


Помни, как выполнять деление многозначных чисел и деление с остатком.
Рассуждаем.
1751 : 5 = 35 (ост. 1) решено неверно, так как первое неполное делимое 17, в частном должно быть 3 цифры.
1983 : 9 = 22 (ост. 3) решено неверно, так как первое неполное делимое 19, в частном должно быть 3 цифры.
2930 : 7 = 41 (ост. 6) решено неверно, так как первое неполное делимое 29, в частном должно быть 3 цифры.
40202 : 6 = 670 (ост. 2) решено неверно, так как первое неполное делимое 40, в частном должно быть 4 цифры.
Выполняем вычисления.
1751 : 5 = 350 (ост. 1)
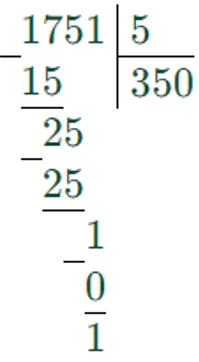
Делим по разрядам, слева направо.
Делим тысячи:
1 : 5 = 0 (ост. 1)
В частное ничего не пишем, а остаток уходит в сотни.
Делим сотни:
В остатке осталась 1 тыс. = 10 сот.
В делимом в разряде сотни 7, получаем 10 + 7 = 17
17 : 5 = 3 (ост. 2)
В частное пишем 1 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 2 сот. = 20 дес.
В делимом в разряде десятков 5, получаем 20 + 5 = 25
25 : 5 = 5
В частном пишем 5 дес.
Делим единицы:
1 : 5 = 0 (ост. 1)
В частном пишем 5 ед.
Остаток 1.
1983 : 9 = 220 (ост. 3)
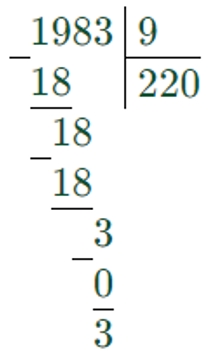
Делим по разрядам, слева направо.
Делим тысячи:
1 : 9 = 0 (ост. 1)
В частное ничего не пишем, а остаток уходит в сотни.
Делим сотни:
В остатке осталась 1 тыс. = 10 сот.
В делимом в разряде сотни 9, получаем 10 + 9 = 19
19 : 9 = 2 (ост. 1)
В частное пишем 2 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 1 сот. = 10 дес.
В делимом в разряде десятков 8, получаем 10 + 8 = 18
18 : 9 = 2
В частном пишем 2 дес.
Делим единицы:
3 : 9 = 0 (ост. 3)
В частном пишем 0 ед.
Остаток 3.
2930 : 7 = 418 (ост. 4)
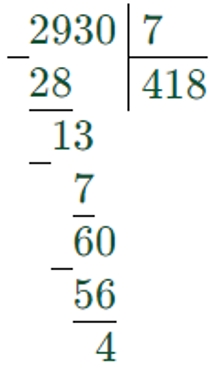
Делим по разрядам, слева направо.
Делим тысячи:
2 : 5 = 0 (ост. 2)
В частное ничего не пишем, а остаток уходит в сотни.
Делим сотни:
В остатке осталась 2 тыс. = 20 сот.
В делимом в разряде сотни 9, получаем 20 + 9 = 29
29 : 7 = 4 (ост. 1)
В частное пишем 4 сот., а остаток уходит в десятки.
Делим десятки:
В остатке осталось 1 сот. = 10 дес.
В делимом в разряде десятков 3, получаем 10 + 3 = 13
13 : 7 = 1 (ост. 6)
В частном пишем 1 дес., а остаток уходит в единицы.
Делим единицы:
В остатке осталось 6 дес. = 60 ед.
В делимом в разряде единиц 0, получаем 60 + 0 = 60
60 : 7 = 8 (ост. 4)
В частном пишем 8 ед.
Остаток 4.
40202 : 6 = 6700 (ост. 2)
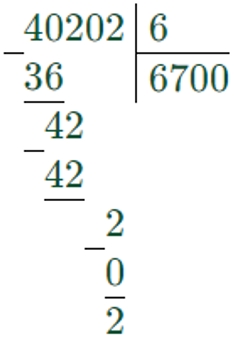
Делим по разрядам, слева направо.
Делим десятки тысяч:
4 : 6 = 0 (ост. 4)
В частное ничего не пишем, а остаток уходит в тысячи.
Делим тысячи:
В остатке осталась 4 дес.тыс. = 40 тыс.
В делимом в разряде тысячи 0, получаем 40 + 0 = 40
40 : 6 = 6 (ост. 4)
В частное пишем 6 тыс., а остаток уходит в сотни.
Делим сотни:
В остатке осталась 4 тыс. = 40 сот.
В делимом в разряде сотни 2, получаем 40 + 2 = 42
42 : 6 = 7
В частное пишем 7 сот.
Делим десятки:
0 : 6 = 0
В частном пишем 0 дес.
Делим единицы:
2 : 6 = 0 (ост. 2)
В частном пишем 0 ед.
Остаток 2.
Оформляем задание в тетрадь.
1751 : 5 = 350 (ост. 1)
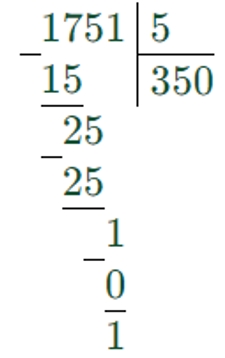
2930 : 7 = 418 (ост. 4)
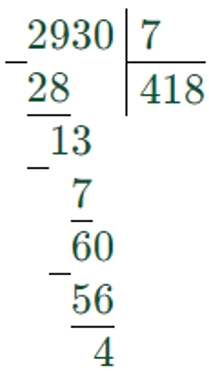
1983 : 9 = 220 (ост. 3)
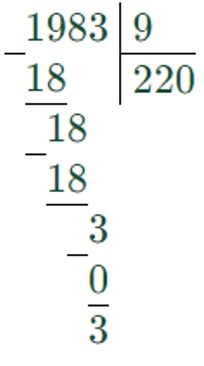
40202 : 6 = 6700 (ост. 2)
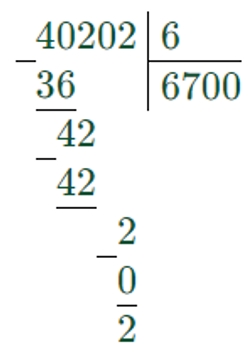
Номер 18.
Ответ:
32340 : 10 = 3234 56400 : 100 = 564
1) Помним о порядке выполнения арифметических действий.
2) Вспомни, как делить многозначные числа столбиком.
3) Вспомни, как складывать и вычитать многозначные числа столбиком.
Выполняем вычисления.
Расставим порядок действий и вычислим по действиям.
4527 ∙ 50 − 710037 : 9 = 147457
Сначала выполняем умножение, затем – деление, а потом вычитание.
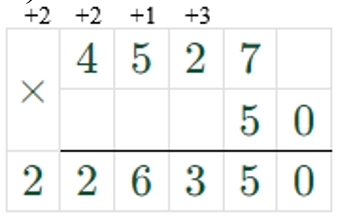
1) 4527 ∙ 50 = 226350
2) 710037 : 9 = 78893
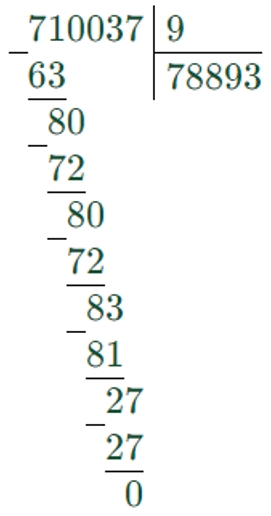
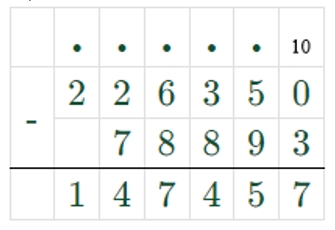
3) 226350 – 78893 = 147457
(932 + 17692) : 6 ∙ 80 = 248320
Сначала выполняем действие в скобках – сложение, затем деление, а потом умножение.
1) 932 + 17692 = 18624
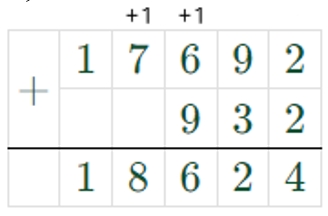
2) 18624 : 6 = 3104
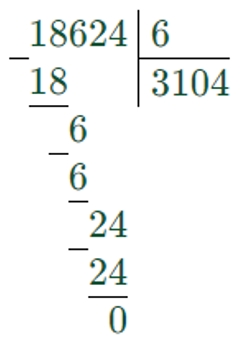
3) 3104 ∙ 80 = 248320
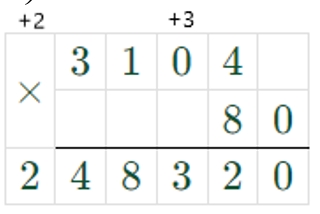
397 ∙ 600 = 238200
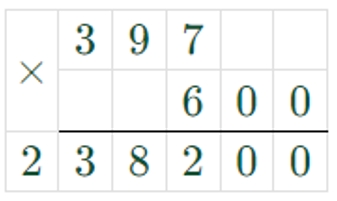
600 = 6 ∙ 100
Достаточно умножить число на 6, а потом приписать справа два нуля.
4030 ∙ 90 = 362700
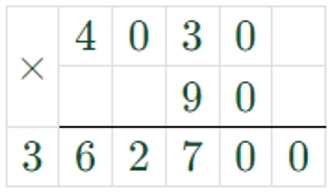
90 = 9 ∙ 10
Достаточно умножить число на 9, а потом приписать справа один нуль.
32340 : 10 = 3234
Чтобы число разделить на 10, то нужно справа отбросить один нуль.
56400 : 100 = 564
Чтобы число разделить на 100, то нужно справа отбросить два нуля.
Оформляем задание в тетрадь.
4527 ∙ 50 − 710037 : 9 = 147457
1) 4527 ∙ 50 = 226350
2) 710037 : 9 = 78893
3) 226350 – 78893 = 147457
(932 + 17692) : 6 ∙ 80 = 248320
1) 932 + 17692 = 18624
2) 18624 : 6 = 3104
3) 3104 ∙ 80 = 248320
397 ∙ 600 = 238200
4030 ∙ 90 = 362700
32340 : 10 = 3234
56400 : 100 = 564
Задание на полях страницы
Начерти узор. Проведи все оси симметрии.
Ответ:
У данной фигуры 4 оси симметрии.
Чтобы проще было перечертить узор, проведи оси симметрии.
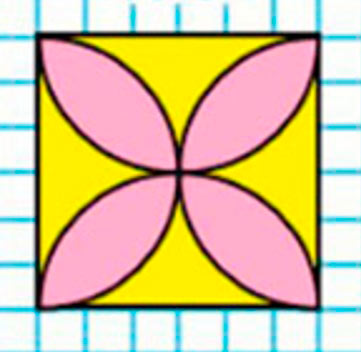
Начертим узор.
Внимательно рассмотри узор на полях страницы, подготовь необходимые инструменты и перечерти его в тетрадь.
Сторона квадрата – 6 клеток.
Проведём оси симметрии.
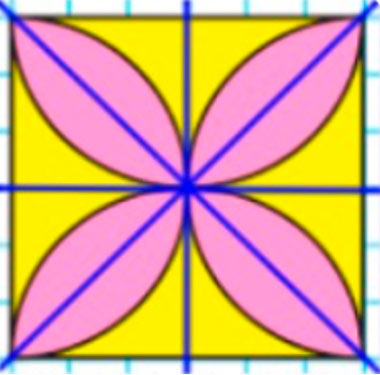
У данной фигуры 4 оси симметрии: вертикальная, горизонтальная и две по диагонали.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.