Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 21
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Математика 4 класс Моро, Волкова - 2 часть страница 21")
Номер 10.
Начерти окружность, проведи в ней диаметр и соедини концы диаметра с любой точкой окружности. Проверь, какого вида треугольник получился.
Ответ:
Получился прямоугольный треугольник.
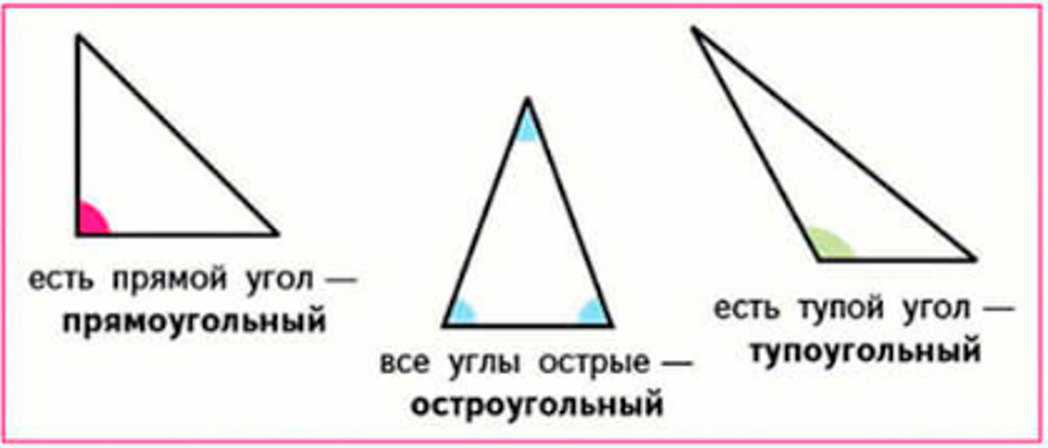
Виды треугольников
1) По видам углов треугольники различаются так:
Начертим окружность и выполним задание.
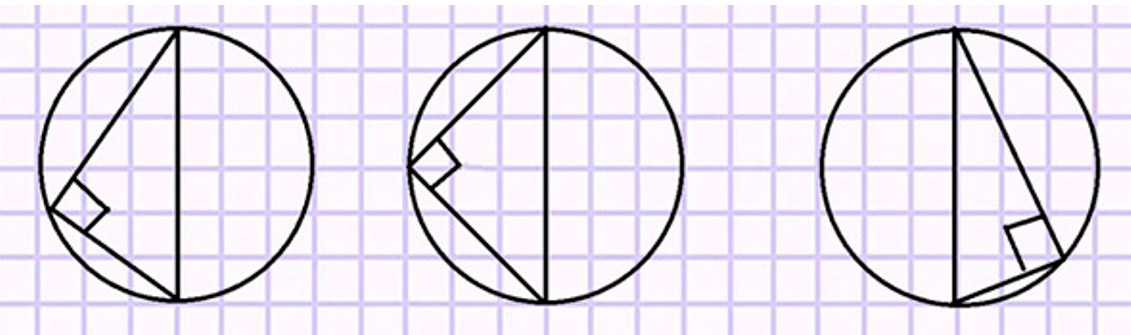
Сделаем вывод.
Какую бы точку на прямой мы не отметили, в результате получается прямоугольный треугольник.
Оформим задание в тетрадь.
Номер 11.
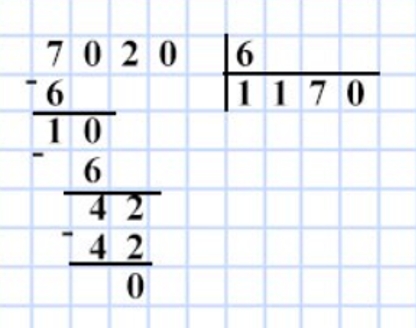
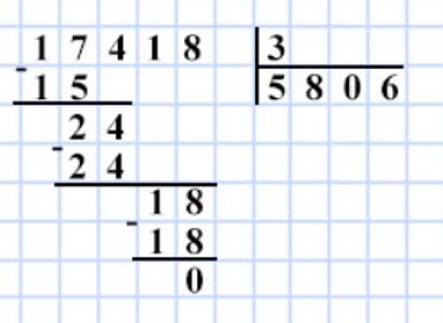
Вычисли значение выражения а : b, если: 1) а = 7020 и b = 6; 2) а = 17418 и b = 3.
Ответ:
Помним алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Выполним вычисления при а = 7 020 и b = 6.
Выполним вычисления при а = 17 418 и b = 3.
Оформим задание в тетрадь.
Номер 12.
Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 100 м. Они встретились через 10 с. Первый мальчик бежал со скоростью 4 м/с. С какой скоростью бежал второй мальчик?
Ответ:
1) 4 ∙ 10 = 40 (м) – пробежал первый мальчик.
2) 100 – 40 = 60 (м) – пробежал второй мальчик.
3) 60 : 10 = 6 (м/с)
Ответ: 6 м/с скорость второго мальчика.
1) 100 : 10 = 10 (м/с) – скорость сближения.
2) 10 – 4 = 6 (м/с)
Ответ: 6 м/с скорость второго мальчика.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
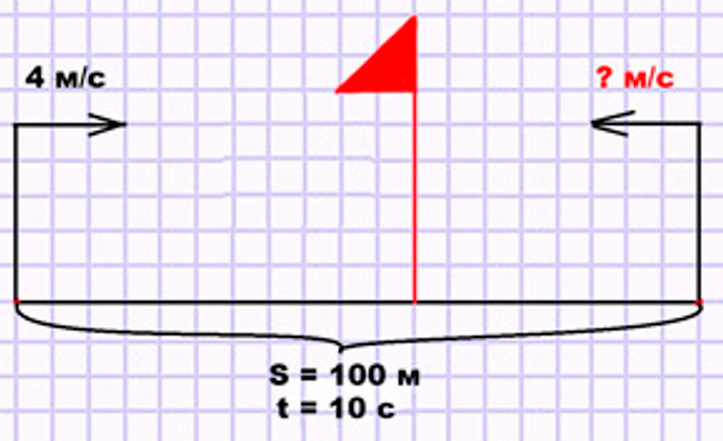
Рассуждаем.
Узнаем, сколько метров пробежал первый мальчик, для этого скорость умножим на время.
1) 4 ∙ 10 = 40 (м) – пробежал первый мальчик.
Продолжаем рассуждение.
Чтобы узнать, сколько метров пробежал второй мальчик, нужно из длины всей дорожки вычесть количество метров, которые пробежал первый мальчик.
2) 100 − 40 = 60 (м) – пробежал второй мальчик.
Продолжаем рассуждение.
Чтобы узнать, с какой скоростью бежал второй мальчик, нужно расстояние, которое он пробежал разделить на время.
3) 60 : 10 = 6 (м/с)
Записываем ответ.
Ответ: 6 м/с скорость второго мальчика.
Номер 13.
Товарный поезд прошёл 315 км. Он был в пути до остановки 3 ч и после остановки 4 ч. Сколько километров прошёл поезд до остановки и сколько после, если он шёл с одинаковой скоростью?
Ответ:
1) 3 + 4 = 7 (ч) – поезд был в пути.
2) 315 : 7 = 45 (км/ч) – скорость поезда.
3) 45 ∙ 3 = 135 (км) – прошел до остановки.
4) 315 − 135 = 180 (км) – прошел после остановки.
Ответ: 135 км прошёл до остановки поезд, 180 км прошёл поезд до остановки и после.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
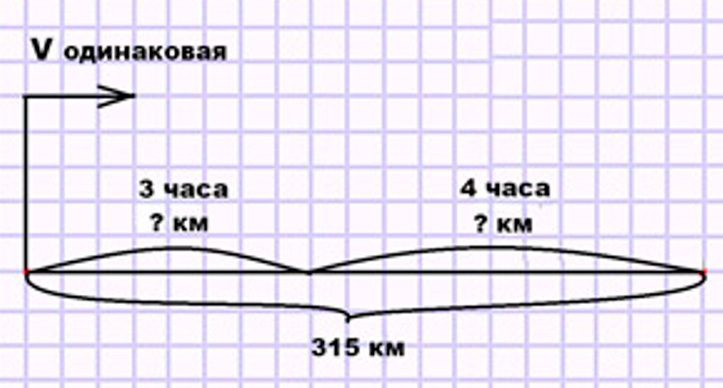
Рассуждаем.
Узнаем, сколько часов поезд был в пути. Для этого сложим время в пути до остановки и после.
1) 3 + 4 = 7 (ч) – поезд был в пути.
Продолжаем рассуждение.
Узнаем скорость поезда, для этого расстояние, которое он прошел разделим на время, которое он был в пути.
2) 315 : 7 = 45 (км/ч) – скорость поезда.
Продолжаем рассуждение.
Теперь узнаем, сколько километров поезд прошел до остановки. Для этого скорость поезда умножим на время, которое он был в пути до остановки.
3) 45 ∙ 3 = 135 (км) – прошел до остановки.
Продолжаем рассуждение.
Чтобы узнать, сколько километров поезд прошел после остановки, нужно из всего расстояния, которое он прошел, вычесть расстояние, которое поезд прошел до остановки.
4) 315 − 135 = 180 (км) – прошел после остановки.
Записываем ответ.
Ответ: 135 км, 180 км.
Номер 14.
Отрезок длиной 90 мм разделили сначала на 3 равные части, а затем каждую из них разделили на 2 равные части. На сколько равных частей разделили весь отрезок? Чему равна длина одной шестой части данного отрезка? Сделай по задаче чертёж и реши её.
Ответ:
Отрезок разделили на 6 равных частей.
90 : 6 = 15 (мм) – длина одной шестой части данного отрезка.
Ответ: на 6 частей всего разделили отрезок, длина одной шестой части данного отрезка составляет 15 мм.
Измерение длины отрезка:
1) Прикладываю линейку к отрезку.
2) Совмещаю нуль на линейке с началом отрезка.
3) Определяю число, соответствующее концу отрезка. Это длина отрезка.
4) Записываю результат измерения.
1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 км = 1000 м
Оформляем условие в виде схематического чертежа.
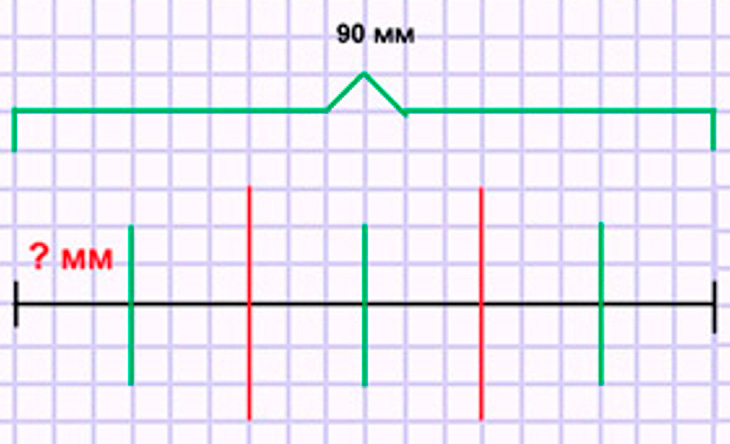
Рассуждаем.
Чтобы узнать, чему равна одна шестая части отрезка, весь отрезок нужно разделить на 6 равных частей.
90 : 6 = 15 (мм) – длина одной шестой части данного отрезка.
Записываем ответ.
Ответ: 6 равных частей, 15 мм.
Номер 15.
Молочный завод отправил в магазин 56 ящиков сливочного масла, по 20 кг в каждом. За день продали одну седьмую часть этого масла. Сколько килограммов масла осталось?
Ответ:
Всего – 56 ящ. по 20 кг
Продали – 
часть
Осталось – ? кг
1) 20 ∙ 56 = 1120 (кг) – масла отправили.
2) 1120 : 7 = 160 (кг) – масла продали.
3) 1120 − 160 = 960 (кг) – масла осталось.
Ответ: 960 кг масла осталось в магазине.
Оформляем условие задачи в виде краткой записи.
Оформляем условие.
Всего – 56 ящ. по 20 кг
Продали – 1/7 часть
Осталось – ? кг
Рассуждаем.
Узнаем, сколько всего килограмм масла отправили в магазин, для этого количество ящиков умножим на количество килограмм в одном ящике.
1) 20 ∙ 56 = 1120 (кг) – отправили масла.
Продолжаем рассуждение.
Узнаем, сколько килограмм масла продали. Для этого массу всего масла разделим на 7, потому что известно, что продали 1/7 часть.
2) 1120 : 7 = 160 (кг) – продали.
Продолжаем рассуждение.
Чтобы узнать, сколько масла осталось после продажи, нужно из всего количества масла вычесть количество проданного.
3) 1120 − 160 = 960 (кг) – осталось.
Записываем ответ.
Ответ: 960 кг.
Номер 16.
Расстояние между городом и зимовкой 150 км. Из города к зимовке выехали аэросани и двигались со скоростью 60 км/ч. В это же время навстречу им из зимовки по той же дороге пошёл лыжник со скоростью 15 км/ч. На каком расстоянии от зимовки он встретил аэросани?
Ответ:
1) 60 + 15 = 75 (км/ч) – скорость сближения.
2) 150 : 75 = 2 (ч) – время пути.
3) 15 ∙ 2 = 30 (км) – на таком расстоянии от зимовки лыжник встретил аэросани.
Ответ: лыжник встретил аэросани на расстоянии от зимовки в 30 км.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
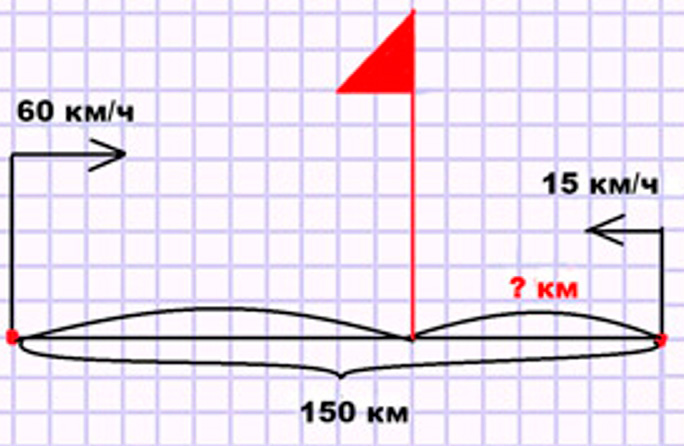
Рассуждаем.
Найдем скорость сближения лыжника с аэросанями. Для этого сложим скорости каждого вместе.
1) 60 + 15 = 75 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Узнаем, какое время они провели в пути до встречи. Для этого расстояние делим на скорость сближения.
2) 150 : 75 = 2 (ч) – время пути.
Продолжаем рассуждение .
Узнаем, на каком расстоянии от зимовки лыжник встретил аэросани. Для этого скорость лыжника умножим на время в пути.
3) 15 ∙ 2 = 30 (км) – на таком расстоянии от зимовки лыжник встретил аэросани.
Записываем ответ.
Ответ: 30 километров.
Номер 17.
Найди ошибки в вычислениях и реши правильно.
Ответ:
1751 : 5 = 35 (ост. 1) решено неверно, так как первое неполное делимое 17, в частном должно быть 3 цифры.
1983 : 9 = 22 (ост. 3) решено неверно, так как первое неполное делимое 19, в частном должно быть 3 цифры.
2930 : 7 = 41 (ост. 6) решено неверно, так как первое неполное делимое 29, в частном должно быть 3 цифры.
40202 : 6 = 670 (ост. 2) решено неверно, так как первое неполное делимое 40, в частном должно быть 4 цифры.
Правильное решение:
Алгоритм деления примеров с остатком:
1) Находим наибольшее число до делимого, которое можно разделить на делитель без остатка.
2) Данное число делим на делитель. Это значение частного.
3) Вычитаем из делимого наибольшее число – это остаток.
4) Проверяем, остаток должен быть меньше делителя.
5) Делаем проверку.
Найдем ошибки в вычислениях.
1751 : 5 = 35 (ост. 1) решено неверно, так как первое неполное делимое 17, в частном должно быть 3 цифры.
1983 : 9 = 22 (ост. 3) решено неверно, так как первое неполное делимое 19, в частном должно быть 3 цифры.
2930 : 7 = 41 (ост. 6) решено неверно, так как первое неполное делимое 29, в частном должно быть 3 цифры.
40202 : 6 = 670 (ост. 2) решено неверно, так как первое неполное делимое 40, в частном должно быть 4 цифры.
Выполним вычисления правильно.
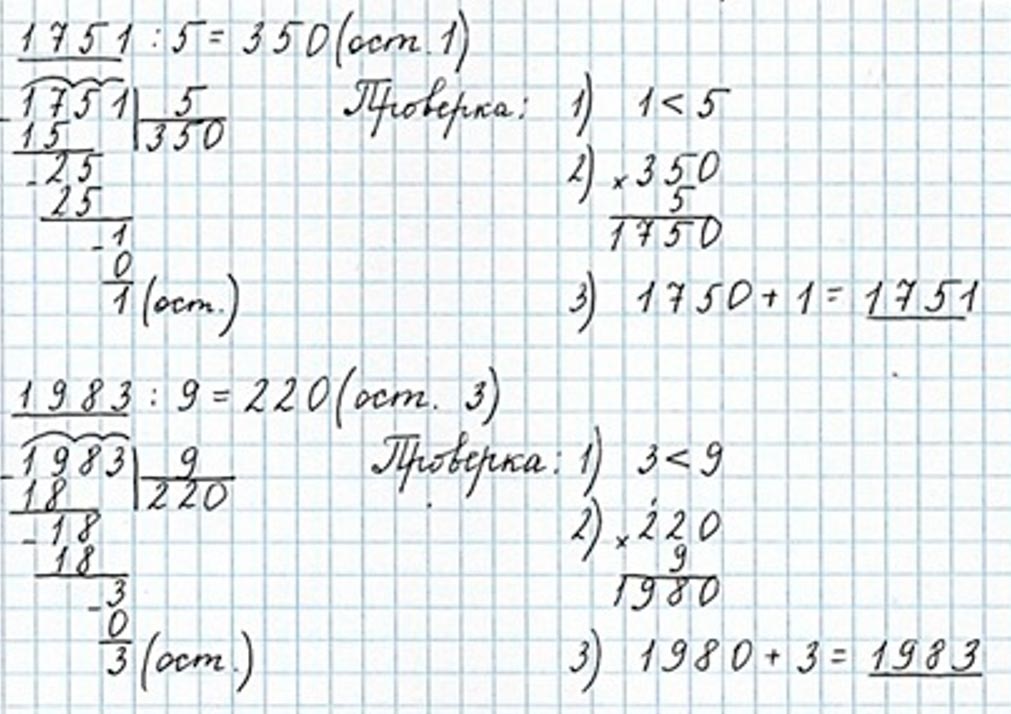
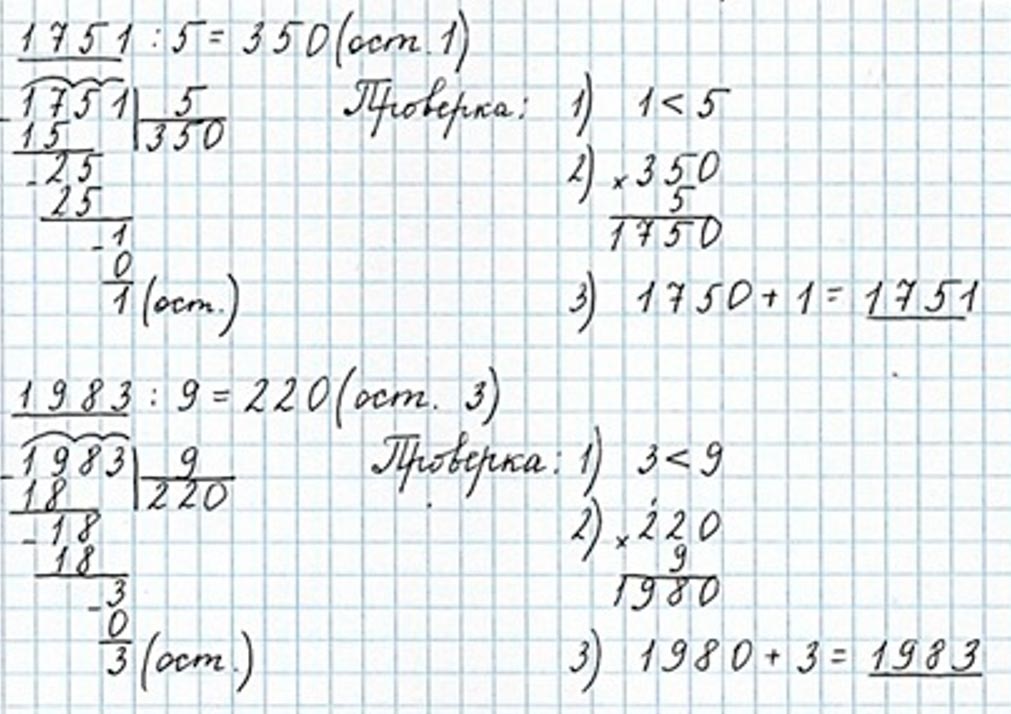
Оформим задание в тетрадь.
Номер 18.
Ответ:
32340 : 10 = 3234 56400 : 100 = 564
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним вычисления по действиям.
Оставшиеся примеры выполняем самостоятельно.
Оформим задание в тетрадь.
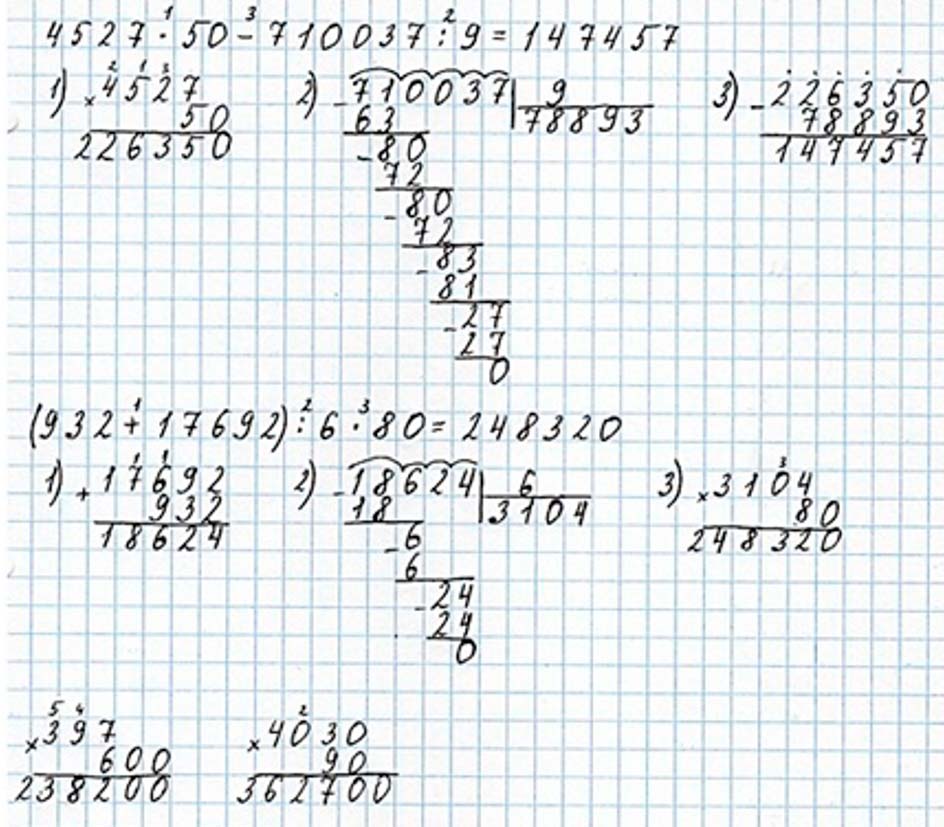
32340 : 10 = 3234
56400 : 100 = 564
Номер 19.
Запиши 5 чисел, каждое из которых делится без остатка и на 5, и на 9.
Ответ:45, 90, 135, 180, 225.
Вспомни названия компонентов действия деления и зависимости между компонентами и результатом действия деления:
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного ∙ делитель = делимое.
Подберем числа, которые без остатка делятся и на 5, и на 9.
Число 45 без остатка делится и на 5, и на 9:
• 45 : 5 = 9
• 45: 9 = 5
Число 90 без остатка делится и на 5, и на 9:
• 90 : 5 = 18
• 90 : 9 = 10
Число 135 без остатка делится и на 5, и на 9:
• 135 : 5 = 27
• 135 : 9 = 15
Число 180 без остатка делится и на 5, и на 9:
•180 : 5 = 36
• 180 : 9 = 20
Число 225 без остатка делится и на 5, и на 9:
• 225 : 5 = 45
• 225 : 9 = 25
Оформим задание в тетрадь.
Ответ: 45, 90, 135, 180, 225.
Задание на полях страницы
Начерти узор
Ответ:
Чтобы проще было перечертить узор, проведи оси симметрии.
Начертим узор.
Внимательно рассмотри узор на полях страницы, подготовь необходимые инструменты и перечерти его в тетрадь.
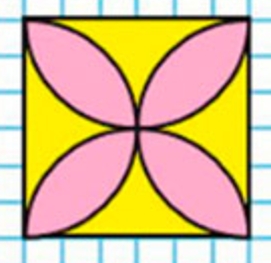
Оформим задание в тетрадь.
Номер 4.
Маша, Оля, Настя и Лена заняли четыре первых места в соревнованиях по плаванию. На вопрос, кто какое место занял, они дали три разных ответа:
Оля – второе, Настя – третье;
Лена – второе, Оля – первое;
Маша – второе, Настя – четвёртое.
Кто какое место занял, если в каждом ответе верной была только одна его часть?
Совет. Начни рассуждать так: «Предположим, что высказывание «Оля - второе» верно, тогда в ответе Маши оба высказывания будут неверными, а это противоречит условию задачи. Значит ...»
Предположим, что высказывание «Оля – второе» верно, тогда в ответе Маши оба высказывания будут неверными, а это противоречит условию задачи. Значит высказывание «Оля – второе» неверное и Настя точно заняла третье место.
Рассмотрим 3-й ответ: мы уже выяснили, что у Насти третье место, значит высказывание «Настя – четвертое» – ложное и поэтому у Маши точно второе место.
Рассмотрим 2-й ответ: мы уже выяснили, что у Маши второе место, значит высказывание «Лена – второе» – ложное и поэтому у Оли точно первое место. Остается только Лена, значит у нее 4 место.
Ответ: 1 место – Оля, 2 место – Маша, 3 место – Настя, 4 – место Лена.
Номер 5.
Для отделки платья ленту длиной 1 м 50 см надо разрезать на несколько частей по 25 см, на несколько частей по 16 см и ещё одну часть длиной 2 см так, чтобы не было обрезков. Определи, как это сделать, и запиши, сколько будет частей по 25 см и сколько будет частей по 16 см.
Ответ:4 части по 25 см, 3 части по 16 см и 1 часть по 2 см.
Номер 6.
Сергей живёт в посёлке и в школу ездит на велосипеде. Занятия в школе начинаются в 9 ч. В 8 ч 40 мин Сергей всегда уже проезжает половину пути от дома до школы. В школу Сергей приезжает за 10 мин до начала занятий. Сколько минут занимает путь Сергея до школы?
Ответ:
1) 9 ч − 10 мин = 8 ч 50 мин – время приезда Сергея в школу.
2) 8 ч 50 мин − 8 ч 40 мин = 10 мин – время затраченное на половину пути.
3) 2 ∙ 10 = 20 мин – занимает путь Сергея до школы.
Ответ: путь Сергея до школы составляет 20 минут.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.