Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 20

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Что узнали. Чему научились
Номер 1.
Объясни приём вычисления.
18 ∙ 20 = 18 ∙ (2 ∙ 10) = (18 ∙ 2) ∙ 10 = 36 ∙ 10 = 360 25 ∙ 12 = 25 ∙ (4 ∙ 3) = (25 ∙ 4) ∙ 3 = 100 ∙ 3 = 300
Ответ:Перестановка и группировка множителей.
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Рассмотрим данные примеры.
18 ∙ 20 = 18 ∙ (2 ∙ 10) = (18 ∙ 2) ∙ 10 = 36 ∙ 10 = 360
25 ∙ 12 = 25 ∙ (4 ∙ 3) = (25 ∙ 4) ∙ 3 = 100 ∙ 3 = 300
Объясним приемы вычисления.
В примерах один из множителей был разбит на два множителя, а затем, перегруппировав полученные множители, было выполнено умножение. Для решения применялось свойство умножения: «От перестановки множителей произведение не изменяется».
Номер 2.
Закончи решение.
Ответ:
1) 35 ∙ 20 = 35 ∙ (2 ∙ 10) = (35 ∙ 2) ∙ 10 = 700
25 ∙ 24 = 25 ∙ (4 ∙ 6) = (25 ∙ 4) ∙ 6 = 600
2) 16 ∙ 30 = 16 ∙ (3 ∙ 10) = (16 ∙ 3) ∙ 10 = 480
42 ∙ 20 = 42 ∙ (2 ∙ 10) = (42 ∙ 2) ∙ 10 = 840
12 ∙ 40 = 12 ∙ (4 ∙ 10) = ( 12 ∙ 4) ∙ 10 = 480
25 ∙ 16 = 5 ∙ 5 ∙ 2 ∙ 8 = (5 ∙ 2) ∙ (5 ∙ 8) = 10 ∙ 40 = 400
15 ∙ 18 = 3 ∙ 5 ∙ 2 ∙ 9 = (5 ∙ 2) ∙ (3 ∙ 9) = 10 ∙ 27 = 270
45 ∙ 14 = 9 ∙ 5 ∙ 2 ∙ 7 = (5 ∙ 2) ∙ (9 ∙ 7) = 10 ∙ 63 = 630
13 ∙ 60 = 13 ∙ (6 ∙ 10) = (13 ∙ 6) ∙ 10 = 780
45 ∙ 20 = 45 ∙ (2 ∙ 10) = (45 ∙ 2) ∙ 10 = 900
15 ∙ 30 = 15 ∙ (3 ∙ 10) = (15 ∙ 3) ∙ 10 = 450
14 ∙ 50 = 2 ∙ 7 ∙ 5 ∙ 10 = (2 ∙ 5) ∙ (7 ∙ 10) = 700
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Рассуждаем.
1. Заменим второй множитель на произведение двух множителей.
2. Используем сочетательное свойство: два соседних множителя можно заменить их произведением.
Удобно группировать множители так, чтобы хотя бы один из множителей был круглым числом.
Закончим решение.
1) 35 ∙ 20 = 35 ∙ (2 ∙ 10) = (35 ∙ 2) ∙ 10 = 700
25 ∙ 24 = 25 ∙ (4 ∙ 6) = (25 ∙ 4) ∙ 6 = 600
2) 16 ∙ 30 = 16 ∙ (3 ∙ 10) = (16 ∙ 3) ∙ 10 = 480
42 ∙ 20 = 42 ∙ (2 ∙ 10) = (42 ∙ 2) ∙ 10 = 840
12 ∙ 40 = 12 ∙ (4 ∙ 10) = ( 12 ∙ 4) ∙ 10 = 480
25 ∙ 16 = 5 ∙ 5 ∙ 2 ∙ 8 = (5 ∙ 2) ∙ (5 ∙ 8) = 10 ∙ 40 = 400
15 ∙ 18 = 3 ∙ 5 ∙ 2 ∙ 9 = (5 ∙ 2) ∙ (3 ∙ 9) = 10 ∙ 27 = 270
45 ∙ 14 = 9 ∙ 5 ∙ 2 ∙ 7 = (5 ∙ 2) ∙ (9 ∙ 7) = 10 ∙ 63 = 630
13 ∙ 60 = 13 ∙ (6 ∙ 10) = (13 ∙ 6) ∙ 10 = 780
45 ∙ 20 = 45 ∙ (2 ∙ 10) = (45 ∙ 2) ∙ 10 = 900
15 ∙ 30 = 15 ∙ (3 ∙ 10) = (15 ∙ 3) ∙ 10 = 450
14 ∙ 50 = 2 ∙ 7 ∙ 5 ∙ 10 = (2 ∙ 5) ∙ (7 ∙ 10) = 700
Оформим задание в тетрадь.
Номер 3.
Сравни выражения и поставь знак >, < или =, чтобы получились верные записи.
Ответ:
18 ∙ 40 = 18 ∙ 4 ∙ 10
18 ∙ 40 = 18 ∙ 40
72 ∙ 14 < 72 ∙ 10 ∙ 4
72 ∙ 14 < 72 ∙ 40
36 ∙ 5 ∙ 10 > 36 ∙ 15
36 ∙ 50 > 36 ∙ 15
98 ∙ 21 = 98 ∙ 3 ∙ 7
98 ∙ 21 = 98 ∙ 21
«>» – знак «больше»
«<» – знак «меньше»
«=» – знак «равно»
Рассуждаем.
Мы видим, что слева и справа есть одинаковые множители, поэтому сравниваем только отличающиеся числа.
Сравним выражения и поставим нужные знаки.
18 ∙ 40 = 18 ∙ 4 ∙ 10
18 ∙ 40 = 18 ∙ 40
72 ∙ 14 < 72 ∙ 10 ∙ 4
72 ∙ 14 < 72 ∙ 40
36 ∙ 5 ∙ 10 > 36 ∙ 15
36 ∙ 50 > 36 ∙ 15
98 ∙ 21 = 98 ∙ 3 ∙ 7
98 ∙ 21 = 98 ∙ 21
Оформим задание в тетрадь.
Номер 4.
Для ремонта квартиры купили 8 рулонов обоев длиной по 10 м 50 см. После ремонта осталась одна четвёртая часть купленных обоев. Сколько метров обоев осталось? Реши задачу разными способами.
Ответ:
Можно оформить в виде чертежа:

1) 10 м 50 см ∙ 8 = 150 см * 8 = 1050 см * 8 = 8400 (см) = 84 (м) – было куплено обоев. 2) 84 : 4 = 21 (м) – обоев осталось.
2-й способ решения:1) 8 : 4 = 2 (р.) – обоев осталось после ремонта. 2) 10 м 50 см ∙ 2 = 1050 м * 2 = 2100 (см) = 21 (м) – обоев осталось после ремонта.
Ответ: 21 м обоев всего остался после ремонта.
Оформляем условие задачи в виде краткой записи или схематического чертежа.
Шаг 1.
Оформляем условие.
Всего – 8 р. по 10 м 50 см
Осталось – 1/4 часть – ? м
Или
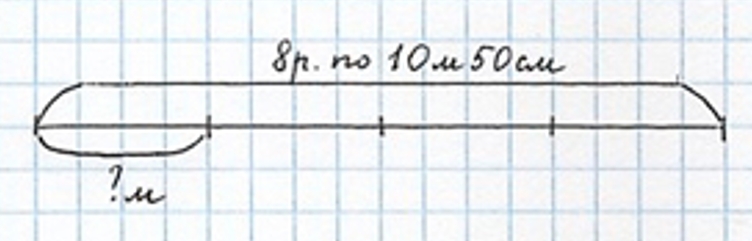
Рассуждаем.
Узнаем, сколько всего было куплено метров обоев, для этого количество метров одного рулона умножаем на количество рулонов.
1) 10 м 50 см ∙ 8 = 84 (м) – было куплено обоев.
Продолжаем рассуждение.
Узнаем, сколько метров обоев осталось, для этого все количество обоев делим на 4, потому что известно, что осталась одна четвертая часть.
2) 84 : 4 = 21 (м) – обоев осталось.
Записываем ответ.
Ответ: 21 м.
Шаг 1.
Рассуждаем.
Узнаем, сколько рулонов обоев осталось после ремонта, для этого количество всех рулонов делим на 4, потому что известно, что осталась одна четвертая часть.
1) 8 : 4 = 2 (р.) – обоев осталось после ремонта.
Продолжаем рассуждение.
Узнаем, сколько метров обоев осталось после ремонта, для этого количество оставшихся рулонов умножаем на количество метров обоев в одном рулоне.
2) 2 ∙ 10 м 50 см = 21 (м) – обоев осталось после ремонта.
Записываем ответ.
Ответ: 21 м.
Номер 5.
Школьная библиотека получила 290 новых учебников в одинаковых пачках. Учебников по русскому языку было 10 пачек, столько же пачек учебников по чтению и 9 пачек учебников по математике. Объясни, что показывают выражения.
Ответ:290 : (10 + 10 + 9) = 10 – количество учебников в одной пачке. 290 : (10 + 10 + 9) ∙ 9 = 90 – количество учебников по математике.
Оформляем условие задачи в виде таблицы, чтобы было проще объяснить, что показывают выражения.
Оформляем условие.

Рассуждаем.
Из таблицы видно, что показывает каждое выражение:
1) 290 : (10 + 10 + 9) = 10 – количество учебников в одной пачке.
2) 290 : (10 + 10 + 9) ∙ 9 = 90 – количество учебников по математике.
Номер 6.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.

200 ∙ 15 ∙ 4 ∙ 5 = (200 ∙ 5) ∙ (15 ∙ 4) = 1 000 ∙ 60 = 60 000
12 ∙ 5 ∙ 250 ∙ 4 = (12 ∙ 5) ∙ (250 ∙ 4) = 60 ∙ 1 000 = 60 000
Оформляем задание в тетрадь.
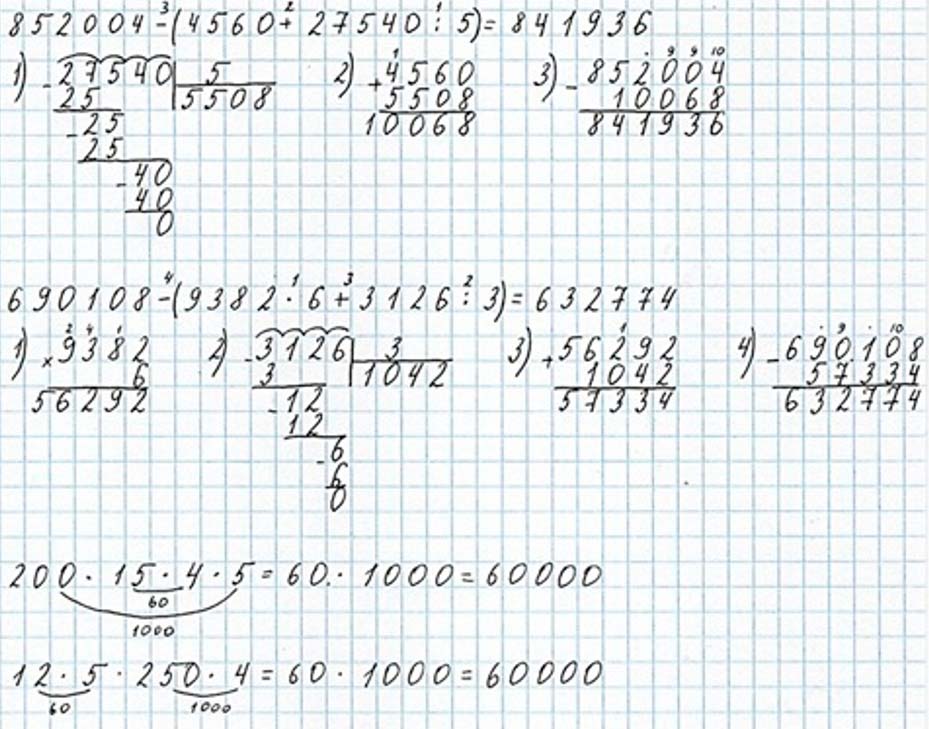
Номер 7.
Рассмотри таблицу и объясни, что обозначают выражения.
1) 30 : 5; 2) 400 : 100; 3) 100 : 5; 4) 100 − 5; 5) 30 : 5 + 400 : 100; 6) 30 : 5 − 400 : 100.

1) Время движения первого объекта. 2) Время движения второго объекта. 3) Во сколько раз скорость второго объекта больше скорости первого. 4) На сколько км/ч скорость второго объекта больше скорости первого. 5) Общее время движения обоих объектов. 6) На сколько больше был в движении первый объект, чем второй.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Рассмотрим таблицу.

Объясним, что обозначают выражения.
1) 30 : 5 – время движения первого объекта.
2) 400 : 100 – время движения второго объекта.
3) 100 : 5 – во столько раз скорость второго объекта больше скорости первого.
4) 100 – 5 – на столько км/ч скорость второго объекта больше скорости первого.
5) 30 : 5 + 400 : 100 – такое время будут двигаться первый и второй объект вместе.
6) 30 : 5 – 400: 100 – на сколько дольше был в движении первый объект, чем второй.
Номер 8.
Выполни деление с остатком и проверку.
Ответ:

Алгоритм деления примеров с остатком.
1) Находим наибольшее число до делимого, которое можно разделить на делитель без остатка.
2) Данное число делим на делитель. Это значение частного.
3) Вычитаем из делимого наибольшее число – это остаток.
4) Проверяем, остаток должен быть меньше делителя.
5) Делаем проверку.
Вспомним как выполнить проверку.
Проверка:
1) Остаток должен быть меньше делителя.
2) Умножим частное на делитель.
3) Прибавим к результату остаток. Сумма должна быть равна делимому.
Выполним вычисления и оформим задание в тетрадь.

Номер 9.
Ответ:


Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполним вычисления по действиям.


Оставшиеся примеры решаем самостоятельно.
Выполняем вычисления и оформляем задание в тетрадь.


Задания на полях страницы
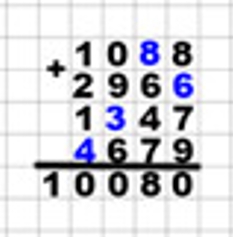
Ребус.


Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить сложение.
Рассмотрим ребус.

Разгадаем ребус.
8 + 7 + 9 = 24. Чтобы получить 0 в единицах, нужно прибавить 6. 24 + 6 = 30.
6 + 4 + 7 = 17, да еще 3 дес. 17 + 3 = 20. Чтобы получить 8 в единицах, нужно прибавить 8. 20 + 8 = 28.
0 + 9 + 6 = 15, да еще 2 сот. 15 + 2 = 17. Чтобы получить 0 в единицах, нужно прибавить 3. 17 + 3 = 20.
1 + 2 + 1 = 4, да еще 2 тыс. 4 + 2 = 6. Чтобы получить 0 в единицах, нужно прибавить 4. 6 + 4 = 10.
Оформим задание в тетрадь.
Реши. Найди лишнее уравнение.

х ∙ 8 = 56
х = 56 : 8
х = 7
Проверка: 7 ∙ 8 = 56
56 = 56
Ответ: х = 7
х ∙ 14 = 98
х = 98 : 14
х = 7
Проверка: 7 ∙ 14 = 98
98 = 98
Ответ: х = 7
84 : х = 12
х = 84 : 12
х = 7
Проверка: 84 : 7 = 12
12 = 12
Ответ: х = 7
5 ∙ х = 35
х = 35 : 5
х = 7
Проверка: 5 ∙ 7 = 35
35 = 35
Ответ: х = 7
х ∙ 7 = 42
х = 42 : 7
х = 6
Проверка: 6 ∙ 7 = 42
42 = 42
Ответ: х = 6
Вывод: лишнее уравнение: х ∙ 7 = 42
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое
Выполняем вычисления.
Решим все уравнения, чтобы определить лишнее.
х ∙ 8 = 56
х = 56 : 8
х = 7
Проверка:
7 ∙ 8 = 56
х ∙ 14 = 98
х = 98 : 14
х = 7
Проверка:
7 ∙ 14 = 98
84 : х = 12
х = 84 : 12
х = 7
Проверка:
84 : 7 = 12
5 ∙ х = 35
х = 35 : 5
х = 7
Проверка:
5 ∙ 7 = 35
х ∙ 7 = 42
х = 42 : 7
х = 6
Проверка:
6 ∙ 7 = 42
Вывод.
Лишним является последнее уравнение, так как у него отличается значение х от всех остальных уравнений.
х ∙ 7 = 42
х = 42 : 7
х = 6 – лишнее уравнение.
Проверка:
6 ∙ 7 = 42
Странички для любознательных
Номер 1.
Витя ждал гостей на день рождения. Вокруг стола поставили несколько табуретов и несколько стульев. У каждого табурета было по 3 ножки, а у каждого стула – по 4. Ребята заняли все стулья и табуреты, и оказалось, что всех ножек – у стульев, табуретов и ребят – 49. Сколько всего ребят было за столом?
Ответ:9 детей, 5 табуретов, 4 стула. 5 ∙ 3 = 15 4 ∙ 4 = 16 9 ∙ 2 = 18 15 + 16 + 18 = 49
Вспомни, как выполняется деление с остатком.
Оформляем краткую запись.
У табурета – 3 ножки
У стула – 4 ножки
У гостя – 2 ноги
Всего – 49 ножек
Сколько ребят было за столом?
Рассуждаем.
Мы знаем, что каждый из ребят обязательно сидел либо на табурете, либо на стуле. Посчитаем, сколько ног (ножек) было у сиденья и сидящего на нём человека всего.
Если человек сидел на табурете:
2 + 3 = 5 (н) – было у табурета и сидящего вместе.
Если человек сидел на стуле:
2 + 4 = 6 (н) – было у стула и сидящего вместе.
Продолжаем рассуждение.
Предположим, что какое-то количество гостей поровну сидело на табуретах и на стульях. Узнаем, сколько ножек будет у пары, если один сидит на стуле, а другой на табурете.
5 + 6 = 11 (н.) – у пары, сидящей на стуле и на табурете.
Продолжаем рассуждение.
Узнаем, сколько таких пар было, разделив общее количество ножек на количество ножек в паре.
49 : 11 = 4 (ост. 5) – пары было.
Значит, 4 ребят сидело на стуле и 4 ребят – на табурете.
Осталось 5 ножек, значит, ещё один человек сидел на табурете.
Делаем вывод.
Получается, что 4 ребят сидело на стуле и 5 ребят сидело на табурете.
4 + 5 = 9 (р.) – было за столом.
Проверим:
4 ∙ 6 + 5 ∙ 5 = 24 + 25 = 49 (ножек) – всего.
Записываем ответ.
Ответ: 9 ребят сидело за столом.
Номер 2.
Крепость окружена стеной, имеющей форму квадрата. На каждой стороне есть ворота, у которых всегда стоят 2 солдата. Начальнику караула нужно усилить охрану так, чтобы у каждой стены было не 2 солдата, а 3, но чтобы общее их число не изменилось. Начальник караула справился с задачей. Попытайся и ты (рис. 1).
Ответ:
Оставляем одного солдата у ворот, а остальных расставляем по углам.
Внимательно рассмотрим рисунок 1 к данному заданию. Подбирая различные варианты, найдем подходящий под наши условия.
Рассуждаем.
Рассмотрим рисунок.
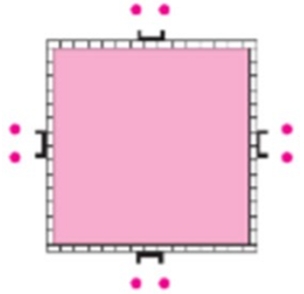
У каждой стены стоят 2 солдата. А требуется, чтобы у каждой стены было по 3 солдата, но их общее число не изменилось.
Продолжаем рассуждение.
Для того, чтобы выполнить это условие, надо оставить по одному солдату у ворот, а остальных расставить по углам крепости.
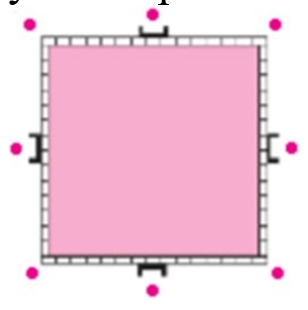
Номер 3.
3. Какое число обозначает каждая буква в квадрате (рис. 2), если известно, что:
1) А в 2 раза меньше, чем С;
2) С равно сумме К и D;
3) К равно разности D и В;
4) D в 3 раза больше, чем В;
5) В в 4 раза меньше, чем 944?
Проверь: сумма всех чисел равна 3186.

1) В = 944 : 4 = 236; 2) D = 236 ∙ 3 = 708; 3) K = 708 − 236 = 472; 4) C = 472 + 708 = 1180; 5) A = 1180 : 2 = 590. Проверка: 236 + 708 + 472 + 1180 + 590 = 3186.
Внимательно рассмотри рисунок к данному заданию. Используя данные задания, ответь на вопросы.
Рассуждаем.
Рассмотрим рисунок к заданию.
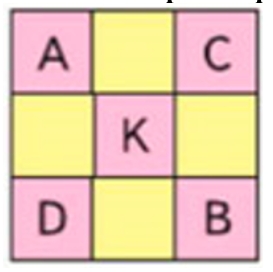
Необходимо найти значение каждой буквы в квадрате.
Известно, что В в 4 раза меньше, чем 944.
Значит, чтобы найти В, нужно 944 разделить на 4.
944 : 4 = 236
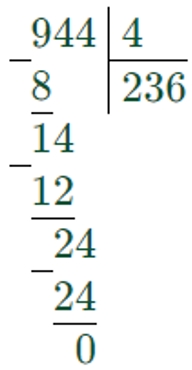
В = 236
Продолжаем рассуждение.
Сказано, что D в 3 раза больше, чем В.
Значит, чтобы найти D, нужно В умножить на 3.
236 ∙ 3 = 708
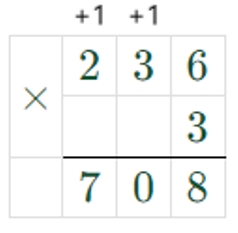
D = 708
Продолжаем рассуждение.
По условию задачи К равно разности D и В.
Значит, чтобы найти К, нужно из D вычесть В.
708 – 236 = 472
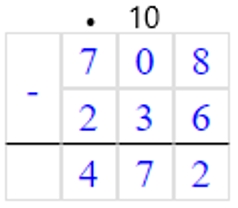
К = 472
Продолжаем рассуждение.
Известно, сто С равно сумме К и D.
Значит, чтобы найти С, нужно к К прибавить D.
472 + 708 = 1180
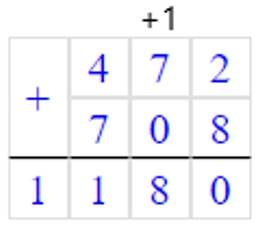
С = 1180
Продолжаем рассуждение.
Сказано, что А в 2 раза меньше, чем С.
Значит, чтобы найти А, нужно С разделить на 2.
1180 : 2 = 590
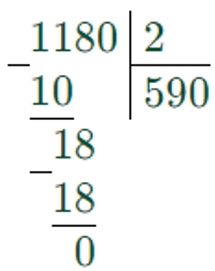
А = 590
Выполним проверку.
Проверка:
236 + 708 + 472 + 1180 + 590 = 3186.
Оформим задание в тетрадь.
1) В = 944 : 4 = 236;
2) D = 236 ∙ 3 = 708;
3) K = 708 − 236 = 472;
4) C = 472 + 708 = 1180;
5) A = 1180 : 2 = 590.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.