Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 19

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 4.
Маша, Оля, Настя и Лена заняли четыре первых места в соревнованиях по плаванию. На вопрос, кто какое место занял, они дали три разных ответа:
Оля – второе, Настя – третье;
Лена – второе, Оля – первое;
Маша – второе, Настя – четвёртое.
Кто какое место занял, если в каждом ответе верной была только одна его часть?
Совет. Начни рассуждать так: «Предположим, что высказывание «Оля - второе» верно, тогда в ответе Лены оба высказывания будут неверными, а это противоречит условию задачи. Значит ...»
Предположим, что высказывание «Оля – второе» верно, тогда в ответе Лены оба высказывания будут неверными, а это противоречит условию задачи. Значит высказывание «Оля – второе» неверное и Настя точно заняла третье место. Рассмотрим 3-й ответ: мы уже выяснили, что у Насти третье место, значит высказывание «Настя – четвертое» – ложное и поэтому у Маши точно второе место. Рассмотрим 2-й ответ: мы уже выяснили, что у Маши второе место, значит высказывание «Лена – второе» – ложное и поэтому у Оли точно первое место. Остается только Лена, значит у нее 4 место.
Ответ: 1 место – Оля, 2 место – Маша, 3 место – Настя, 4 – место Лена.
Используя рисунок и данные к заданию, дай ответы на вопросы.
Рассуждаем.
Предположим, что высказывание «Оля – второе» верно, тогда в ответе Лены оба высказывания будут неверными, а это противоречит условию задачи. Значит высказывание «Оля – второе» неверное и Настя точно заняла третье место.
Продолжаем рассуждение.
Рассмотрим 3-й ответ: мы уже выяснили, что у Насти третье место, значит высказывание «Настя – четвертое» – ложное и поэтому у Маши точно второе место.
Продолжаем рассуждение.
Рассмотрим 2-й ответ: мы уже выяснили, что у Маши второе место, значит высказывание «Лена – второе» – ложное и поэтому у Оли точно первое место. Остается только Лена, значит у нее 4 место.
Записываем ответ.
Ответ: 1 место – Оля, 2 место – Маша, 3 место – Настя, 4 – место Лена.
Номер 5.
Для отделки платья ленту длиной 1 м 50 см надо разрезать на несколько частей по 25 см, на несколько частей по 16 см и ещё одну часть длиной 2 см так, чтобы не было обрезков. Догадайся, как это сделать, и запиши, сколько будет частей по 25 см и сколько будет частей по 16 см.
Ответ:4 части по 25 см, 3 части по 16 см и 1 часть по 2 см.
Оформляем условие задачи в виде таблицы.
Оформляем условие.

Рассуждаем.
• 1 м 50 см = 150 (см) – длина всей ленты.
• 150 – 2 = 148 (см) – общая длина отрезов 1 и 2 типа ( по 25 см и по 16 см).
Предположим, что самое большое количество отрезов было 1 типа, то есть длиной 25 см:
• 148 : 25 = 5 (ост. 23). Это значит, что из ленты данной длины можно отрезать самое большее 5 отрезов по 25 см.
• 25 ∙ 5 = 125 (см) – потребуется на 5 отрезов по 25 см.
• 148 – 125 = 23 (см) – останется на отрезы длиной 16 см.
• 23 : 16 = 1 (ост. 7) (шт) – количество отрезов по 16 см.
• Так как количество отрезов не может быть числом с остатком, то это предположение неверно.
Продолжаем рассуждение.
Предположим, что количество отрезов было 1 типа, то есть длиной 25 см, было 4 штуки:
• 25 ∙ 4 = 100 (см) потребуется на 4 отреза по 25 см.
• 148 – 100 = 48 (см) – останется на отрезы длиной 16 см.
• 48 : 16 = 3 (шт) – количество отрезов по 16 см.
• Значит могло быть 4 отреза по 25 см и 3 отреза по 16 см.
Продолжаем рассуждение.
Предположим, что количество отрезов было 1 типа, то есть длиной 25 см, было 3 штуки:
• 25 ∙ 3 = 75 (см) – потребуется на 3 отреза по 25 см.
• 148 – 75 = 73 (см) – останется на отрезы длиной 16 см.
• 73 : 16 = 4 (ост. 9) (шт) – количество отрезов по 16 см,
• Так как количество отрезов не может быть числом с остатком, то это предположение неверно.
Продолжаем рассуждение.
Предположим, что количество отрезов было 1 типа, то есть длиной 25 см, было 2 штуки:
• 25 ∙ 2 = 50 (см) – потребуется на 2 отреза по 25 см.
• 148 – 50 = 98 (см) – останется на отрезы длиной 16 см.
• 98 : 16 = 6 (ост. 2) (шт) – количество отрезов по 16 см.
• Так как количество отрезов не может быть числом с остатком, то это предположение неверно.
Делаем вывод.
Итак, существует только один возможный вариант раскройки ленты длиной 150 см:
• 4 отреза по 25 см
• 3 отреза по 16 см
• 1 отрез длиной 2 см.
Записываем ответ.
Ответ: 4 части по 25 см и 3 части по 16 см.
Номер 6.
Сергей живёт в посёлке и в школу ездит на велосипеде. Занятия в школе начинаются в 9 ч. В 8 ч 40 мин Сергей всегда уже проезжает половину пути от дома до школы. В школу Сергей приезжает за 10 мин до начала занятий. Сколько минут занимает путь Сергея до школы?
Ответ:
1) 9 ч − 10 мин = 8 ч 50 мин – время приезда Сергея в школу.
2) 8 ч 50 мин − 8 ч 40 мин = 10 мин – время затраченное на половину пути.
3) 2 ∙ 10 = 20 мин – занимает путь Сергея до школы.
Ответ: 20 минут всего занимает путь Сергея до школы.
Оформляем условие задачи в виде схематического чертежа.
Оформляем условие.
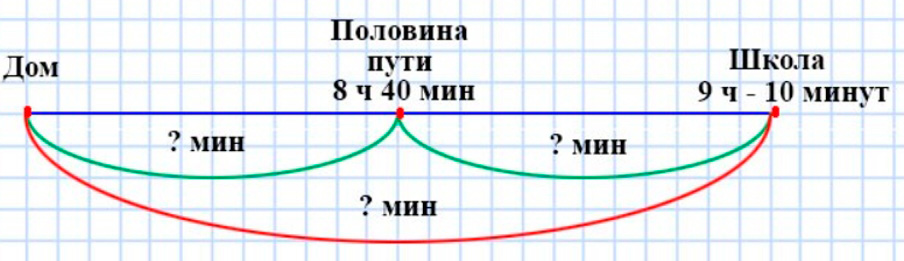
Рассуждаем.
Чтобы узнать время приезда Сергея в школу, нужно из времени, когда начинаются занятия вычесть 10 минут.
1) 9 ч − 10 мин = 8 ч 50 мин – время приезда Сергея в школу.
Продолжаем рассуждение.
Чтобы узнать, сколько Сергей тратит на половину пути, нужно из времени приезда в школу вычесть время, когда Сергей проезжает половину пути.
2) 8 ч 50 мин − 8 ч 40 мин = 10 мин – время, затраченное на половину пути.
Продолжаем рассуждение.
Если время затраченное на половину пути до школы умножить на 2, мы получим количество времени, которое тратит Сергей на дорогу из дома до школы каждый день.
3) 2 ∙ 10 = 20 мин – занимает путь Сергея до школы.
Записываем ответ.
Ответ: 20 минут.
Прямоугольный параллелепипед
Номер 76.
1) Изготовь модель прямоугольного параллелепипеда, используя его развертку (рис. 1). Вспомни план действий при изготовлении модели куба, составь план действий по изготовлению модели прямоугольного параллелепипеда и выполни его.
Поверхность прямоугольного параллелепипеда состоит из прямоугольников, их называют гранями прямоугольного параллелепипеда. Стороны граней называют ребрами, а вершины граней − вершинами прямоугольного параллелепипеда (рис. 2).
2) Сосчитай, сколько у прямоугольного параллелепипеда граней, сколько ребер, сколько вершин.
3) Сравни куб и прямоугольный параллелепипед.
1) План действий по изготовлении модели прямоугольного параллелепипеда:
• Перечерти на клетчатую бумагу фигуру (рис.1).
• Вырежи её.
• Перегни по красным линиям, намажь клеем «язычки» и склей.
2) У прямоугольного параллелепипеда 6 граней, 12 ребер и 8 вершин.
3) У куба все грани – это равные квадраты, а у прямоугольного параллелепипеда – это прямоугольники.
Повтори материал о прямоугольнике.
Рассуждаем.
Рассмотрим модель прямоугольного параллелепипеда.
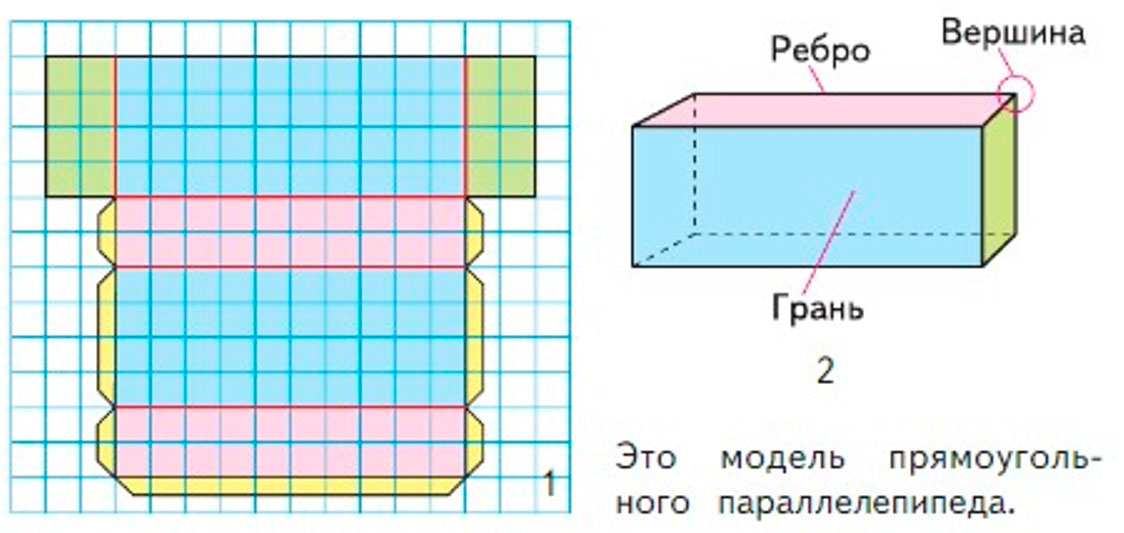
Изготовим по плану прямоугольный параллелепипед.
План изготовления прямоугольного параллелепипеда:
1) перенесём на клетчатую бумагу развертку;
2) вырежем её;
3) прогнём развертку по красным линиям сгиба;
4) намажем клеем язычки для склеивания (обозначенные желтым цветом);
5) склеим модель.
Продолжаем рассуждения.
Сосчитаем количество граней, ребер и вершин параллелепипеда.
У прямоугольного параллелепипеда – 6 граней, 12 рёбер и 8 вершин.
Продолжаем рассуждения.
У куба и прямоугольного параллелепипеда одинаковое количество граней, рёбер и вершин.
У куба все грани – это квадраты, а у прямоугольного параллелепипеда – прямоугольники.
Номер 77.
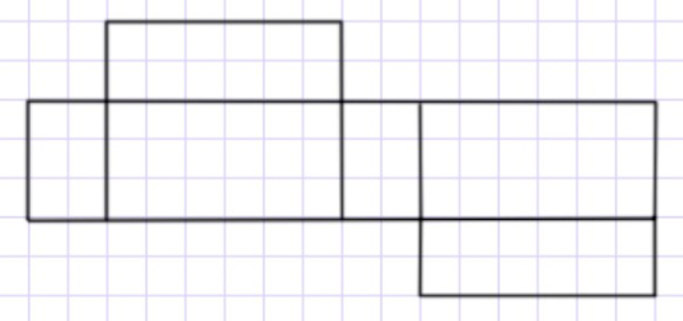
Является ли фигура (рис. 3) разверткой прямоугольного параллелепипеда?
Ответ:Данная фигура не является разверткой прямоугольного параллелепипеда, так как ей не хватает одной грани.
Повтори материал о прямоугольнике.
Рассуждаем.
Рассмотрим фигуру.
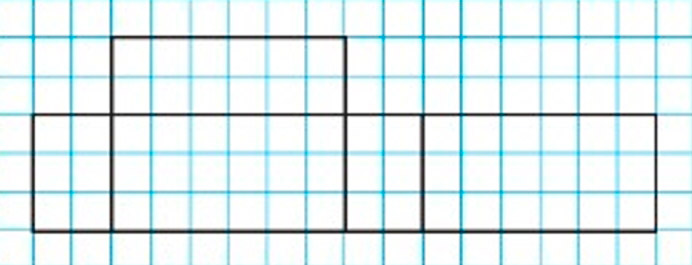
Продолжаем рассуждения.
Данная фигура не является разверткой прямоугольного параллелепипеда, потому что граней у неё всего 5, а должно быть 6.
Задание внизу страницы.
Начерти в тетради такую фигуру, как в задании 77. Дополни ее так, чтобы она стала разверткой прямоугольного параллелепипеда.
Ответ:
Вспомни, что такое развёртка, и как из неё можно сделать прямоугольный параллелепипед.
Рассуждаем.
Начертим в тетради такую фигуру, как в задании 77.
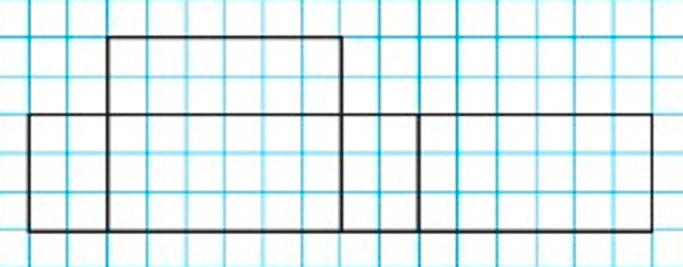
Мы выяснили, что данная фигура не является развёрткой прямоугольного параллелепипеда.
Продолжаем рассуждения.
Дополним фигуру так, чтобы она стала развёрткой прямоугольного параллелепипеда. Для этого начертим недостающую грань.
Задание на полях страницы.
От какого из этих предметов может быть такая тень на стене?
Ответ:Такая тень может быть у аквариума.
Повтори материал о прямоугольнике.
Рассуждаем.
Рассмотрим рисунки.

От какого из этих предметов может быть такая тень на стене?
Продолжаем рассуждения.
Длина тени равна 5 клеток, а ширина – 3 клетки.
Сравним размеры тени с размерами рисунков.
Заметим, что грань аквариума таких же размеров, что и тень.
Следовательно, тень на стене может быть от аквариума.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.