Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 18

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Номер 1.
Витя ждал гостей на день рождения. Вокруг стола поставили несколько табуретов и несколько стульев. У каждого табурета было по 3 ножки, а у каждого стула – по 4. Ребята заняли все стулья и табуреты, и оказалось, что всех ножек – у стульев, табуретов и ребят – 49. Сколько всего ребят было за столом?
Ответ:
9 детей, 5 табуретов, 4 стула.
3 ∙ 5 = 15 (шт.) – ножек в табуретов.
4 ∙ 4 = 16 (шт.) – ножек у стульев.
2 ∙ 9 = 18 (шт.) – ножек у ребят
15 + 16 + 18 = 49
Ответ: всего 9 ребят за столом.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
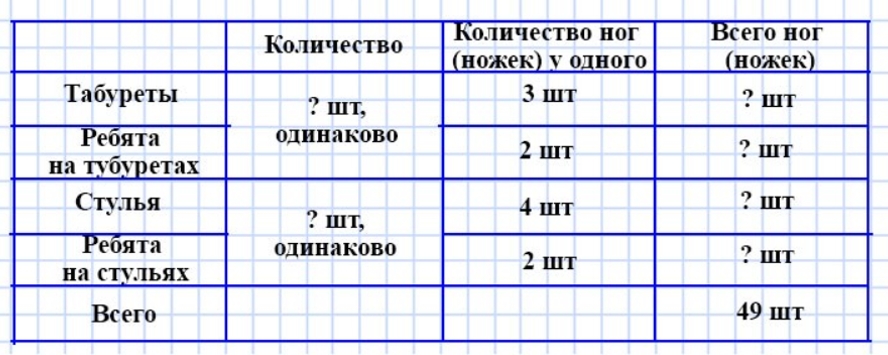
Рассуждаем.
Мы знаем, что каждый из ребят обязательно сидел либо на табурете, либо на стуле.
Посчитаем, сколько ног (ножек) было у сиденья и сидящего на нём человека всего:
• если человек сидел на табурете:
2 + 3 = 5 (шт) – ног (ножек) было у табурета и ребёнка вместе;
• если человек сидел на стуле:
2 + 4 = 6 (шт) – ног (ножек) было у стула и ребёнка вместе.
Продолжаем рассуждение.
Предположим, что большинство детей сидело на стульях:
• 49 : 6 = 7 (ост. 5). Это значит 7 стульев было бы в этом случае.
• 7 ∙ 6 = 42 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 42 = 5 (шт) – ног осталось.
• 5 : 5 = 1 (шт) – количество табуретов.
• Значит 7 детей могло сидеть на стульях, а 1 человек мог сидеть на табурете. В этом случае было всего 7 + 1 = 8 ребят.
Продолжаем рассуждение.
Предположим, что стульев было меньше 7, например, что стульев было 6. Тогда:
• 6 ∙ 6 = 36 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 36 = 13 (шт) – ног осталось.
• 13 : 5 = 2 (ост. 3) – количество табуретов.
• Так как количество табуретов с остатком быть не может, то это предположение неверно.
Продолжаем рассуждение.
Предположим, что стульев было 5. Тогда:
• 5 ∙ 6 = 30 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 30 = 19 (шт) – ног осталось.
• 19 : 5 = 3 (ост. 4) – количество табуретов.
• Так как количество табуретов с остатком быть не может, то это предположение неверно.
Продолжаем рассуждение.
Предположим, что стульев было 4. Тогда:
• 4 ∙ 6 = 24 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 24 = 25 (шт) –ног осталось.
• 25 : 5 = 5 – количество табуретов.
• Значит, 4 ребёнка могло сидеть на стульях, а 5 человек могли сидеть на табуретах. В этом случае было всего 4 + 5 = 9 ребят.
Продолжаем рассуждение.
Предположим, что стульев было 3. Тогда:
• 3 ∙ 6 = 18 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 18 = 31 (шт) – ног осталось.
• 31 : 5 = 10 (ост. 1) – количество табуретов.
• Так как количество табуретов с остатком быть не может, то это предположение неверно.
Продолжаем рассуждение.
Предположим, что стульев было 2. Тогда:
• 2 ∙ 6 = 12 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 12 = 35 (шт) – ног осталось.
• 35 : 5 = 7 – количество табуретов.
• Значит 2 ребёнка могло сидеть на стульях, а 7 человек мог сидеть на табуретах. В этом случае было всего 2 + 7 = 9 ребят.
Продолжаем рассуждение.
Предположим, что стул был 1. Тогда:
• 1 ∙ 6 = 6 (шт) – ног было у стульев и ребят, которые на них сидели.
• 49 – 6 = 43 (шт) – ног осталось.
• 43 : 5 = 8 (ост. 3) – количество табуретов.
• Так как количество табуретов с остатком быть не может, то это предположение неверно.
Вывод.
Итак, существует три возможных варианта:
1. 7 стульев, 1 табурет, 8 ребят;
2. 4 стула, 5 табуретов, 9 ребят;
3. 2 стула, 7 табуретов, 9 ребят.
Так как в условии задачи сказано, что «несколько ребят сидело на табуретах», то первый возможный вариант с 1 табуретом нам не подходит, а во втором и третьем варианте количество ребят – 9 человек. Значит правильный ответ – 9 человек.
Записываем ответ.
Ответ: за столом сидело 9 ребят.
Номер 2.
Крепость окружена стеной, имеющей форму квадрата. На каждой стороне есть ворота, у которых всегда стоят 2 солдата. Начальнику караула нужно усилить охрану так, чтобы у каждой стены было не 2 солдата, а 3, но чтобы общее их число не изменилось. Начальник караула справился с задачей. Попытайся и ты (рис. 1).
Ответ:
 Оставляем одного солдата у ворот, а остальных расставляем по углам.
Оставляем одного солдата у ворот, а остальных расставляем по углам.
Внимательно рассмотрим рисунок 1 к данному заданию. Подбирая различные варианты, найдем подходящий под наши условия.
Рассуждаем.
Для того, чтобы выполнить это условие, надо оставить по одному солдату у ворот, а остальных расставить по углам здания.
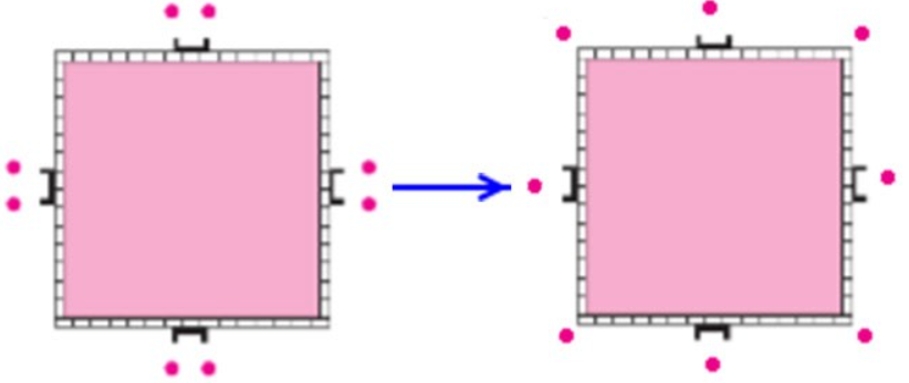
Оформляем задание в тетрадь
Номер 3.
3. Какое число обозначает каждая буква в квадрате (рис. 2), если известно, что:
1) А в 2 раза меньше, чем С;
2) С равно сумме К и D;
3) К равно разности D и В;
4) D в 3 раза больше, чем В;
5) В в 4 раза меньше, чем 944?
Проверь: сумма всех чисел равна 3186.

1) В = 944 : 4 = 236;
2) D = 236 ∙ 3 = 708;
3) K = 708 − 236 = 472;
4) C = 472 + 708 = 1180;
5) A = 1180 : 2 = 590.
Проверка: 236 + 708 + 472 + 1180 + 590 = 3186.
Внимательно рассмотрим рисунок 2 к данному заданию. Используя данные задания, ответим на вопросы.
Рассмотрим рисунок к заданию.
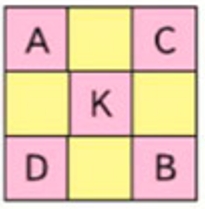
Ответим на вопросы.
1) В = 944 : 4 = 236;
2) D = 236 ∙ 3 = 708;
3) K = 708 − 236 = 472;
4) C = 472 + 708 = 1180;
5) A = 1180 : 2 = 590.
Выполним проверку.
Проверка:
236 + 708 + 472 + 1180 + 590 = 3186.
Куб
Номер 73.
1) Изготовь модель куба по такому плану: перечерти на клетчатую бумагу фигуру (рис. 1). Это развертка куба. Вырежи ее, перегни по красным линиям, намажь клеем «язычки» и склей.
Поверхность куба состоит из квадратов, их называют гранями куба. Стороны граней называют ребрами, а вершины граней − вершинами куба (рис. 2).
2) Сосчитай, сколько у куба граней, сколько ребер, сколько вершин.
3) Хватит ли листа цветной бумаги, площадь которого 1 дм2, чтобы обклеить изготовленный куб со всех сторон? Совет: Определи по развертке, чему равна сумма площадей всех граней куба.
1) Выполнив все указанные действия, вы получите куб.
2) У куба 6 граней, 12 ребер и 8 вершин.
3) Сторона грани куба равна 2 см.
1) 2 · 2 = 4 (см2) − площадь одной грани куба;
2) 4 · 6 = 24 (см2) − площадь всей поверхности куба;
1 дм2 = 100 см2
100 см2 > 24 см2 – листа цветной бумаги хватит, чтобы обклеить изготовленный куб.
Ответ: листа цветной бумаги хватит, чтобы обклеить куб.
Повтори единицы площади.
Изготовим модель куба по плану.
Переведя на клетчатую бумагу данную развертку, аккуратно вырезаем ее, не забывая о язычках для склеивания.
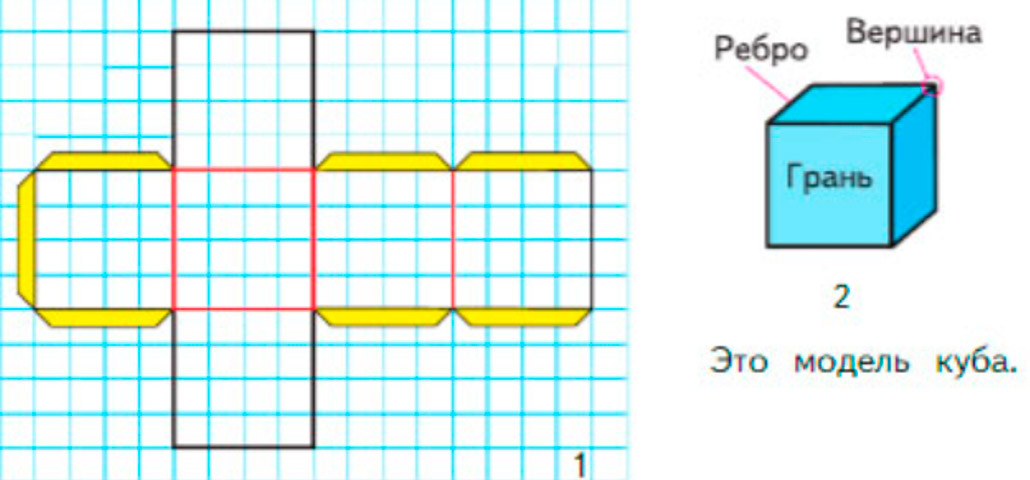
После этого аккуратно прогибаем ее по всем красным линиям и линиям сгиба язычков для склеивания (можно воспользоваться ножницами ли линейкой и чуть надавливая продавить линии сгибов).
Клеем смазать язычки, обозначенные на схеме развертки желтым цветов.
В результате мы получили такое объемное тело, как куб, изображенный на рисунке.
Рассуждаем.
Сосчитаем грани, ребра и вершины у куба.
Грани куба – это квадраты, из которых и состоит поверхность куба.
У куба 6 граней.
Ребра – это линии, расположенные по бокам всех граней куба.
У куба 12 рёбер.
Вершины – это точки, расположенные по углам граней.
У куба 8 вершин.
Продолжаем рассуждения.
Найдем с помощью развертки сумму площадей всех граней куба. Так как куб состоит из 6 граней и все они квадраты, то, чтобы найти площадь поверхности куба, нужно площадь одной грани умножить на 6.
Согласно рисунку, сторона квадрата равно 2 см.
2 ∙ 2 = 4 (см²) – площадь одной грани;
4 ∙ 6 = 24 (см²) – площадь всех граней куба.
Площадь листа бумаги, которым хотят обклеить куб – 1 дм²
1 дм² = 100 см².
100 см² > 24 см², значит, листа цветной бумаги в 1 дм² хватит, чтобы обклеить куб со всех сторон.
Номер 74.
Какая фигура может быть развёрткой куба?
Ответ:Развёрткой куба может быть фигура 1.
Вспомни, что такое развёртка, и как из неё можно сделать куб.
Рассуждаем.
Рассмотрим фигуры.
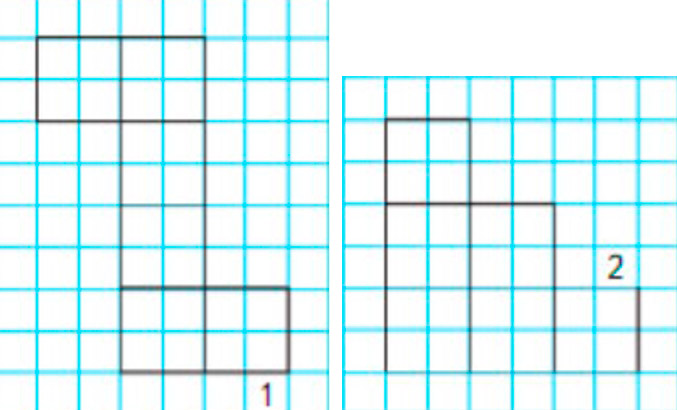
Если вырезать фигуру 1 и согнуть её по линиям, то получится куб. Значит, фигура 1 – это развёртка куба.
Если вырезать фигуру 2 и согнуть её по линиям, то не получится склеить куб. Значит, фигура 2 не может быть развёрткой куба.
Оформим задание в тетрадь.
Ответ: развёрткой куба может быть фигура 1.
Номер 75.
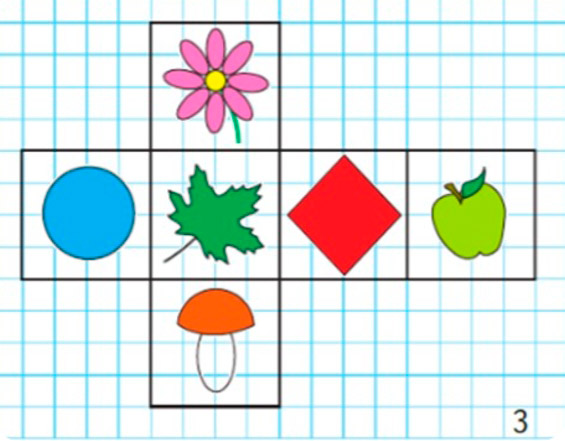
Начерти в тетради такую же развертку куба (рис. 3). Нарисуй на ней заданные предметы и геометрические фигуры так, чтобы напротив друг друга были: круг и квадрат; лист и яблоко; гриб и цветок.
Ответ:
Повтори материал о квадрате.
Чертим развёртку.
Начертим в тетради развертку куба из учебника.
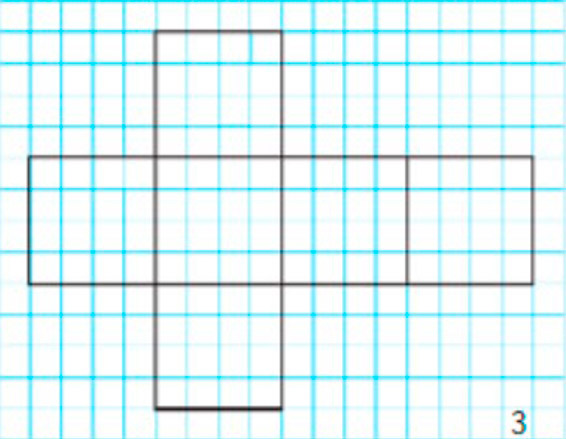
Рисуем предметы.
Нарисуем на развёртке заданные предметы и геометрические фигуры так, чтобы напротив друг друга были: круг и квадрат, лист и яблоко, гриб и цветок.
Задание вверху страницы
Назови предметы, которые имеют форму куба.
Ответ:Шкатулка, игральные кости, коробка, дом.
Вспомни, что такое куб.
Рассуждаем.
Куб – это правильный многогранник, каждая грань которого представляет собой квадрат. Все рёбра куба равны.
Вспомним, какие предметы могут иметь форму куба.
Это может быть шкатулка, игральные кости, коробка, дом.
Оформим задание в тетрадь.
Шкатулка, игральные кости, коробка, дом.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.