Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 17

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Перестановка и группировка множителей
Задание вверху страницы
Вспомни свойства умножения (с. 118, п. 1, 2). Объясни, почему верны следующие равенства:
5 ∙ 7 ∙ 2 = 5 ∙ 2 ∙ 7
25 ∙ 3 ∙ 4 ∙ 9 = 25 ∙ 4 ∙ 3 ∙ 9
15 ∙ (2 ∙ 6) = 15 ∙ 2 ∙ 6
25 ∙ (7 ∙ 4) = 25 ∙ 4 ∙ 7
Равенства в первом столбике верны потому, что от перестановки множителей произведение не меняется. Равенства во втором столбике верны, так как они решены с использованием сочетательного свойства (при группировке множителей любым способом, произведение не меняется.
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Объясним, почему верны равенства первого столбика.
Равенства в первом столбике верны потому, что от перестановки множителей произведение не меняется.
Объясним, почему верны равенства второго столбика.
Равенства во втором столбике верны, так как они решены с использованием сочетательного свойства (при группировке множителей любым способом, произведение не меняется).
Номер 65.
Объясни, как вычислили произведения.
Ответ:1) 25 ∙ 47 ∙ 4 = 25 ∙ 4 ∙ 47 = 100 ∙ 47 = 4700 2) 7 ∙ 50 ∙ 6 ∙ 2 = (7 ∙ 6) ∙ (50 ∙ 2) = 42 ∙ 100 = 4200 Произведение искали удобным способом, пытаясь привести произведение из нескольких множителей к произведению из двух, один из которых сотня.
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Внимательно рассмотрим данные вычисления.
1) 25 ∙ 47 ∙ 4 = 25 ∙ 4 ∙ 47 = 100 ∙ 47 = 4700
2) 7 ∙ 50 ∙ 6 ∙ 2 = (7 ∙ 6) ∙ (50 ∙ 2) = 42 ∙ 100 = 4200
Объясним, как вычислили первое произведение.
25 ∙ 47 ∙ 4 = 25 ∙ 4 ∙ 47 = 100 ∙ 47 = 4700
От перемены мест множителей произведение не меняется, поэтому сначала умножим 25 на 4 и получим 100, а затем уже 100 умножим на 47, приписав к числу 47 два нуля.
Объясним, как вычислили второе произведение.
7 ∙ 50 ∙ 6 ∙ 2 = (7 ∙ 6) ∙ (50 ∙ 2) = 42 ∙ 100 = 4200
От перемены мест множителей произведение не меняется, поэтому сгруппируем множители так, чтобы сначала умножить 7 на 6, выполнив обычное табличное умножение и получив 42, потом 50 умножим на 2, получим 100, а затем умножим 42 на 100, приписав к числу 42 два нуля.
Сделаем вывод.
Произведение искали удобным способом, пытаясь привести произведение из нескольких множителей к произведению из двух, один из которых сотня.
Номер 66.
(Устно.) Вычисли удобным способом.
Ответ:
8 ∙ 4 ∙ 25 ∙ 5 = (8 ∙ 5) ∙ (25 ∙ 4) = 40 ∙ 100 = 4000
9 ∙ 15 ∙ 6 ∙ 10 = (9 ∙ 10) ∙ (15 ∙ 6) = 90 ∙ 90 = 8100
15 ∙ 7 ∙ 4 ∙ 10 = (15 ∙ 4) ∙ (7 ∙ 10) = 60 ∙ 70 = 4200
8 ∙ 7 ∙ 5 ∙ 3 = (8 ∙ 5) ∙ (7 ∙ 3) = 40 ∙ 21 = 840
25 ∙ 3 ∙ 8 ∙ 4 = (25 ∙ 4) ∙ (3 ∙ 8) = 100 ∙ 24 = 2400
35 ∙ 6 ∙ 5 ∙ 2 = (35 ∙ 2) ∙ (6 ∙ 5) = 70 ∙ 30 = 2100.
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Рассуждаем.
Использовали переместительное свойство: от перестановки множителей произведение не изменится и сочетательное свойство: два соседних множителя можно заменить их произведением.
Группируем множители так, чтобы последним действием умножать на круглое число.
Выполним вычисления, используя правило в подсказке.
8 ∙ 4 ∙ 25 ∙ 5 = (4 ∙ 25) ∙ (8 ∙ 5) = 100 ∙ 40 = 4000
9 ∙ 15 ∙ 6 ∙ 10 = (15 ∙ 6) ∙ (9 ∙ 10) = 90 ∙ 90 = 8100
15 ∙ 7 ∙ 4 ∙ 10 = (15 ∙ 4) ∙ (7 ∙ 10) = 60 ∙ 70 = 4200
8 ∙ 7 ∙ 5 ∙ 3 = (8 ∙ 5) ∙ (7 ∙ 3) = 40 ∙ 21 = 840
25 ∙ 3 ∙ 8 ∙ 4 = (25 ∙ 4) ∙ (3 ∙ 8) = 100 ∙ 24 = 2400
35 ∙ 6 ∙ 5 ∙ 2 = (6 ∙ 5) ∙ (35 ∙ 2) = 30 ∙ 70 = 2100
Проверим себя.
Номер 67.
Из двух городов, расстояние между которыми 520 км, одновременно вышли навстречу друг другу два поезда и встретились через 4 ч. Один поезд шёл со скоростью 60 км/ч. С какой скоростью шёл другой поезд?
Ответ:
1) 60 ∙ 4 = 240 (км) – прошёл 1-й поезд. 2) 520 − 240 = 280 (км) – прошёл другой поезд. 3) 280 : 4 = 70 (км/ч)
2-й способ решения:1) 520 : 4 = 130 (км/ч) – скорость сближения. 2) 130 – 60 = 70 (км/ч)
Ответ: 70 км/ч скорость другого поезда.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
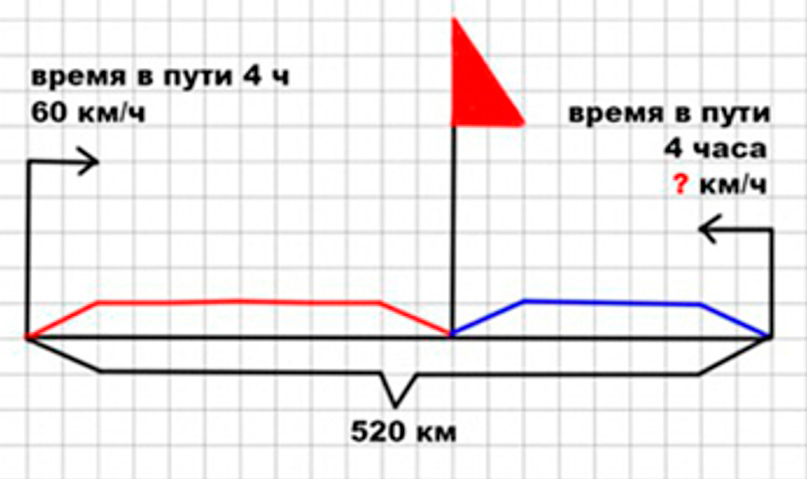
Рассуждаем.
Найдем скорость сближения поездов. Для этого, расстояние между городами разделим на количество часов, через которые они встретились.
1) 520 : 4 = 130 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Теперь мы сможем узнать скорость другого поезда. Для этого из скорости сближения поездов вычитаем скорость первого поезда.
2) 130 – 60 = 70 (км/ч)
Записываем ответ.
Ответ: 70 км/ч скорость другого поезда.
Номер 68.
От двух пристаней, расстояние между которыми 120 км, одновременно отошли навстречу друг другу два теплохода. Один из них шёл со скоростью 22 км/ч, другой – со скоростью 18 км/ч. Через сколько часов теплоходы встретились? Какое расстояние прошёл до встречи каждый теплоход?
Ответ:
1) 22 + 18 = 40 (км/ч) – скорость сближения теплоходов.
2) 120 : 40 = 3 (ч) – время, через которое встретились теплоходы.
3) 22 ∙ 3 = 66 (км) – прошёл 1-ый теплоход.
4) 18 ∙ 3 = 54 (км) – прошёл 2-ой теплоход.
Ответ: через 3 ч встретились теплоходы, 66 км всего прошёл первый теплоход и 54 км всего прошёл второй теплоход.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Оформляем условие в виде схематического чертежа.
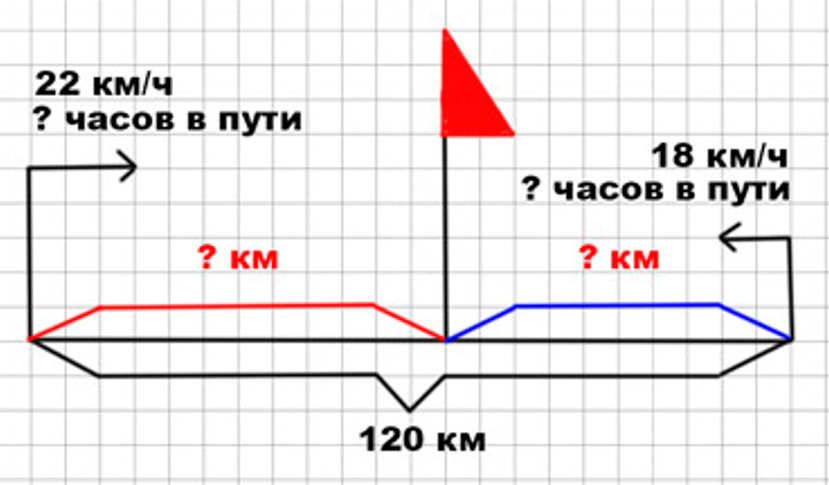
Рассуждаем.
Найдем скорость сближения теплоходов. Для этого сложим скорости обоих теплоходов вместе.
1) 22 + 18 = 40 (км/ч) – скорость сближения теплоходов.
Продолжаем рассуждение.
Найдем время, через которое встретились теплоходы. Для этого расстояние делим на скорость сближения.
2) 120 : 40 = 3 (ч) – время, через которое встретились теплоходы.
Продолжаем рассуждение.
Узнаем, какое расстояние до встречи прошел первый теплоход. Для этого скорость умножим на количество часов в пути.
3) 22 ∙ 3 = 66 (км) – прошёл 1-ый теплоход.
Продолжаем рассуждение.
Узнаем, какое расстояние до встречи прошел второй теплоход. Для этого скорость умножим на количество часов в пути.
4) 18 ∙ 3 = 54 (км) – прошёл 2-ой теплоход.
Записываем ответ.
Ответ: 3 ч, 66 км и 54 км.
Номер 69.
Мише вместе с папой 42 года, его брату Саше вместе с папой 40 лет, а всем им вместе 50 лет. Узнай, сколько лет каждому из них.
Ответ:
1) 50 − 40 = 10 (лет) – Мише. 2) 42 − 10 = 32 (года) – папе.

3) 50 − 42 = 8 (лет) – Саше.
Ответ: Мише – 10 лет, Саше – 8 лет, папе – 32 года.
Оформляем условие задачи в виде схематического чертежа.
Оформляем условие.

Рассуждаем.
Узнаем, сколько лет Мише. Для этого из общего возраста вычтем возраст Саши и папы вместе.
1) 50 − 40 = 10 (лет) – Мише.
Продолжаем рассуждение.
Узнаем, сколько лет папе. Для этого из общего возраста Миши и папы вычтем возраст Миши.
2) 42 − 10 = 32 (года) – папе.
Продолжаем рассуждение.
Узнаем, сколько лет Саше. Для этого из общего возраста вычтем возраст Миши и папы вместе.
3) 50 − 42 = 8 (лет) – Саше.
Записываем ответ.
Ответ: Мише – 10 лет, Саше – 8 лет, папе – 32 года.
Номер 70.
Начерти прямой угол с вершиной в точке О. Отложи от точки О на сторонах угла равные отрезки ОА и ОВ длиной по 3 см. Соедини отрезком точки А и В. Какого вида треугольник получился? Дай два ответа.
Ответ:
1) Треугольник АОВ – прямоугольный. 2) Треугольник АОВ – равнобедренный.
Виды треугольников
1) По видам углов треугольники различаются так:
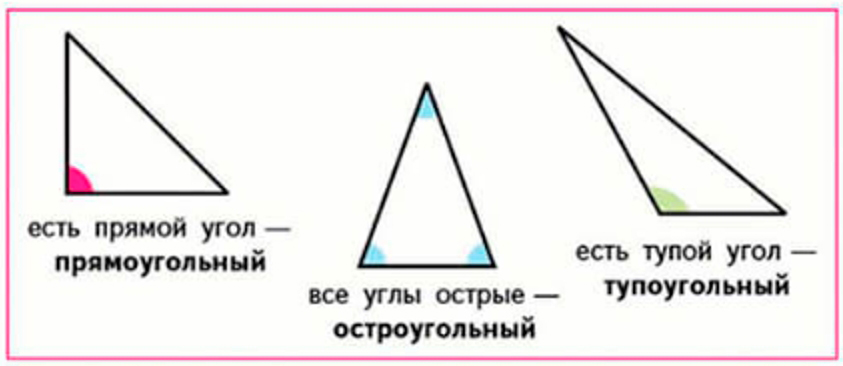
2) Треугольники различаются по тому, равны ли длины сторон:
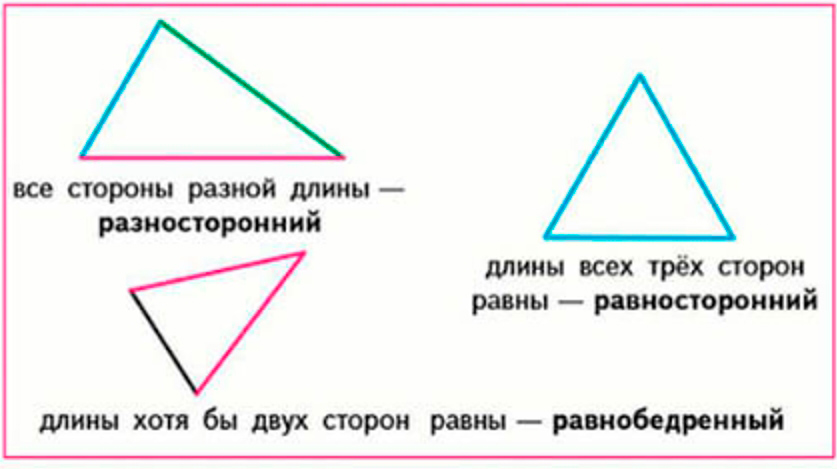
Начертим треугольник.
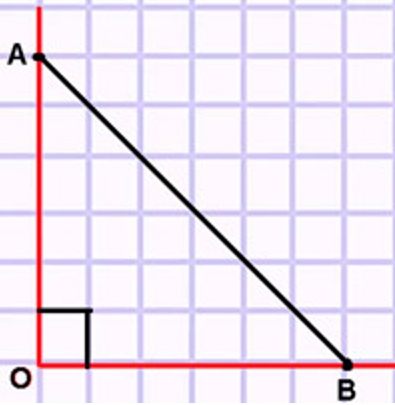
Ответим на вопросы.
1) Треугольник ОАВ равнобедренный, так как стороны ОА = ОВ = 3 см.
2) Треугольник ОАВ прямоугольный, так как угол АОВ = 90°
Номер 71.
Ответ:


Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.


Оформляем задание в тетрадь.

Номер 72.
Проверь, что число 7560 делится без остатка на все однозначные числа.
Ответ:7560 : 1 = 7560

Помним алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.
Рассуждаем.
Если число разделить на 1, то получится число, которое делили.
На ноль делить нельзя.
Выполняем вычисления и оформляем задание в тетрадь.
7560 : 1 = 7560

Задание внизу страницы
Вычисли.
Ответ:16 ∙ 8 ∙ 2 ∙ 5 = (16 ∙ 5) ∙ (8 ∙ 2) = 80 ∙ 16 = 1280 7 ∙ 2 ∙ 13 ∙ 5 = (7 ∙ 13) ∙ (2 ∙ 5) = 91 ∙ 10 = 910
1) От перестановки множителей произведение не изменяется.
2) Два соседних множителя можно заменять их произведением.
3) При умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
Выполняем вычисления с пояснением.
16 ∙ 8 ∙ 2 ∙ 5 = (16 ∙ 8) ∙ (2 ∙ 5) = 128 ∙ 10 = 1 280
7 ∙ 2 ∙ 13 ∙ 5 = (13 ∙ 7) ∙ (2 ∙ 5) = 91 ∙ 10 = 910
Используем сочетательное свойство: два соседних множителя можно заменить их произведением.
Удобно группировать множители так, чтобы хотя бы один из множителей был круглым числом.
Оформляем задание в тетрадь.
16 ∙ 8 ∙ 2 ∙ 5 = (16 ∙ 5) ∙ (8 ∙ 2) = 80 ∙ 16 = 1280
7 ∙ 2 ∙ 13 ∙ 5 = (7 ∙ 13) ∙ (2 ∙ 5) = 91 ∙ 10 = 910
Задание на полях страницы

Сравни площади фигур.

Площадь розовой фигуры – 17 клеток Площадь жёлтой фигуры – 18 клеток 17 < 18 Площадь розовой фигуры меньше, площадь жёлтой фигуры.
Внимательно считай клеточки.
Рассмотрим фигуры на полях.
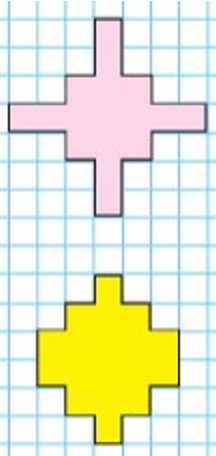
Сравним данные фигуры.
Посчитаем количество клеточек, которые занимают фигуры.
Площадь розовой фигуры – 17 клеток
Площадь жёлтой фигуры – 18 клеток
17 < 18, значит площадь розовой фигуры меньше, чем площадь жёлтой фигуры.
Площадь какой фигуры больше?

Площадь розовой фигуры – 17 клеток
Площадь жёлтой фигуры – 18 клеток
17 < 18
Площадь жёлтой фигуры больше, чем площадь розовой фигуры.
Ответ: площадь жёлтой фигуры больше площади розовой фигуры.
Внимательно посчитай клеточки.
Рассмотрим фигуры на полях.
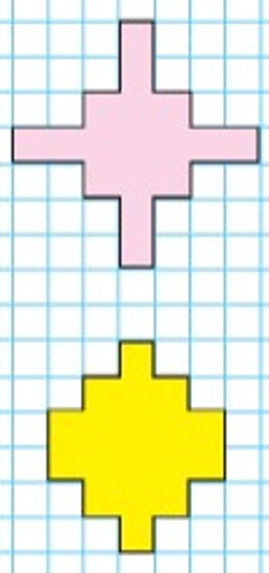
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой.
Сравним данные фигуры.
Посчитаем количество клеточек, которые занимают фигуры.
Площадь розовой фигуры – 17 клеток
Площадь жёлтой фигуры – 18 клеток
18 > 17, значит, площадь жёлтой фигуры больше, чем площадь розовой фигуры.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.