Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 16

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 61.
Реши задачи, сравни решения.
1) Два лыжника вышли одновременно навстречу друг другу из двух посёлков и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч, а второй – со скоростью 14 км/ч. Найди расстояние между посёлками.
2) Из двух посёлков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шёл со скоростью 12 км/ч, а второй – со скоростью 14 км/ч. Через сколько часов лыжники встретились?
3) Из двух посёлков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч. С какой скоростью шёл второй лыжник?



Задача 1:
1) 12 + 14 = 26 (км/ч) – скорость сближения.
2) 26 ∙ 3 = 78 (км)
Ответ: 78 км расстояние между посёлками.
Задача 2:
1) 12 + 14 = 26 (км/ч) – скорость сближения.
2) 78 : 26 = 3 (ч)
Ответ: 3 часа лыжники шли.
Задача 3:
1) 78 : 3 = 26 (км/ч) – скорость сближения.
2) 26 − 12 = 14 (км/ч)
Ответ: 14 км/ч скорость второго лыжника.
Сравнение решений:
Эти задачи можно считать обратными друг другу.
В первой задаче необходимо найти расстояние между поселками. Для этого использовали формулу для нахождения, зная общее время движения и скорость сближения:
t ∙ (V1 + V2) = S.
Во второй задаче необходимо найти время движения при известных скоростях сближения и расстоянии. Для этого применяем формулу:
t = S : (V1 + V2).
В третьей задаче нужно найти одну из скоростей сближения при известных времени, расстоянии и одной скорости. Использовали следующую формулу:
V2 = (S : t) − V1.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Рассмотрим схематический чертеж к задаче.
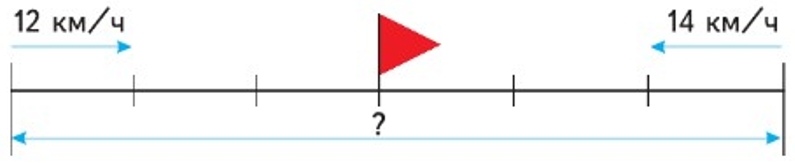
Рассуждаем.
Найдем скорость сближения. Для этого сложим скорости каждого лыжника вместе.
1) 12 + 14 = 26 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы узнать расстояние между поселками, нужно скорость сближения лыжников умножить на время, через которое они встретились.
2) 26 ∙ 3 = 78 (км)
Записываем ответ.
Ответ: 78 км расстояние между посёлками.
Шаг 1.
Рассмотрим схематический чертеж к задаче.
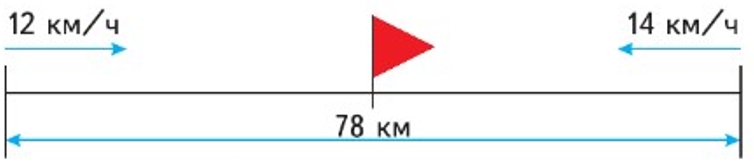
Рассуждаем.
Найдем скорость сближения. Для этого сложим скорости каждого лыжника вместе.
1) 12 + 14 = 26 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы узнать через какое время лыжники встретились, нужно расстояние разделить на скорость сближения.
2) 78 : 26 = 3 (ч)
Записываем ответ.
Ответ: 3 часа лыжники шли.
Шаг 1.
Рассмотрим схематический чертеж к задаче.
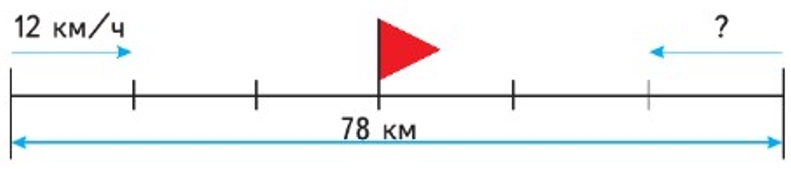
Рассуждаем.
Найдем скорость сближения. Для этого расстояние разделим на скорость первого лыжника.
1) 78 : 3 = 26 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы найти скорость второго лыжника, нужно из скорости сближения вычесть скорость первого лыжника.
2) 26 − 12 = 14 (км/ч)
Записываем ответ.
Ответ: 14 км/ч скорость второго лыжника.
Шаг 1.
Рассуждаем.
Эти задачи можно считать обратными друг другу.
В первой задаче необходимо найти расстояние между поселками. Для этого использовали формулу для нахождения, зная общее время движения и скорость сближения:
t ∙ (V1 + V2) = S.
Во второй задаче необходимо найти время движения при известных скоростях сближения и расстоянии. Для этого применяем формулу:
t = S : (V1 + V2).
В третьей задаче нужно найти одну из скоростей сближения при известных времени, расстоянии и одной скорости. Использовали следующую формулу:
V2 = (S : t) − V1.
Оформляем задание в тетрадь.
Номер 62.
Составь и реши три похожие задачи про пешеходов, которые шли навстречу друг другу со скоростями 4 км/ч и 5 км/ч и встретились через 2 ч.
Ответ:Задача 1: Из двух посёлков одновременно навстречу друг другу вышли два пешехода и встретились через 2 часа. Один пешеход шел со скоростью 4 км/ч, другой – 5 км/ч. Какое расстояние между поселками?
1-й способ решения:1) 4 ∙ 2 = 8 (км) – прошёл 1-ый пешеход. 2) 5 ∙ 2 = 10 (км) – прошёл 2-ой пешеход. 3) 8 + 10 = 18 (км)
2-й способ решения:1) 4 + 5 = 9 (км/ч) – скорость сближения. 2) 9 ∙ 2 = 18 (км)
Ответ: 18 км расстояние между посёлками.
Задача 2:
Из двух посёлков одновременно навстречу друг другу вышли два пешехода: один со скоростью 4 км/ч, а другой – со скоростью 5 км/ч. Расстояние между посёлками 18 км. Через сколько часов пешеходы встретятся?
1) 4 + 5 = 9 (км/ч) – скорость пешеходов.
2) 18 : 9 = 2 (ч)
Ответ: через 2 часа пешеходы встретятся.
Задача 3:
Из двух посёлков одновременно навстречу друг другу вышли два пешехода и встретились через 2 ч. Расстояние между посёлками 18 км. Первый пешеход шёл со скоростью 4 км/ч. С какой скоростью шёл второй пешеход.
1) 4 ∙ 2 = 8 (км) – прошёл 1-ый пешеход. 2) 18 − 8 = 10 (км) – прошёл 2-ой пешеход. 3) 10 : 2 = 5 (км/ч)
2-й способ решения:1) 18 : 2 = 9 (км/ч) - скорость сближения. 2) 9 – 4 = 5 (км/ч)
Ответ: 5 км/ч скорость второго пешехода.
S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Шаг 1.
Составляем условие первой задачи.
Из двух посёлков одновременно навстречу друг другу вышли два пешехода и встретились через 2 часа. Один пешеход шел со скоростью 4 км/ч, другой – 5 км/ч. Какое расстояние между поселками?
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Найдем скорость сближения. Для этого сложим скорости каждого пешехода вместе.
1) 4 + 5 = 9 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы узнать расстояние между поселками, нужно скорость сближения пешеходов умножить на время, через которое они встретились.
2) 9 ∙ 2 = 18 (км)
Записываем ответ.
Ответ: 18 км расстояние между посёлками.
Шаг 1.
Составляем условие второй задачи.
Из двух посёлков одновременно навстречу друг другу вышли два пешехода: один со скоростью 4 км/ч, а другой – со скоростью 5 км/ч. Расстояние между посёлками 18 км. Через сколько часов пешеходы встретятся?
Оформляем условие в виде схематического чертежа.
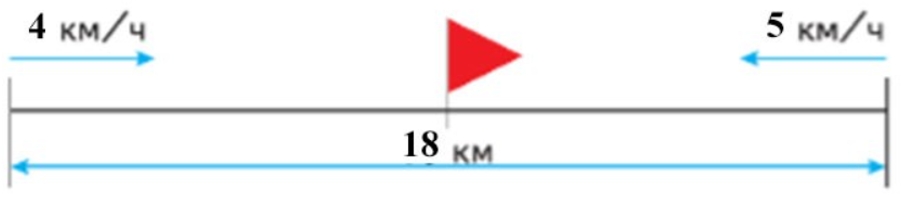
Рассуждаем.
Найдем скорость сближения. Для этого сложим скорости каждого пешехода вместе.
1) 4 + 5 = 9 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы узнать через какое время пешеходы встретились, нужно расстояние разделить на скорость сближения.
2) 18 : 9 = 2 (ч)
Записываем ответ.
Ответ: 2 часа пешеходы встретятся.
Шаг 1.
Составляем условие третьей задачи.
Из двух посёлков одновременно навстречу друг другу вышли два пешехода и встретились через 2 ч. Расстояние между посёлками 18 км. Первый пешеход шёл со скоростью 4 км/ч. С какой скоростью шёл второй пешеход.
Оформляем условие в виде схематического чертежа.
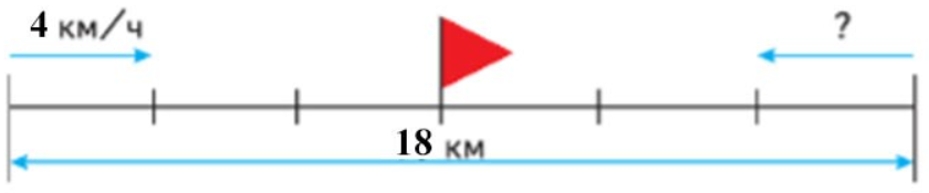
Рассуждаем.
Найдем скорость сближения. Для этого расстояние разделим на время.
1) 18 : 2 = 9 (км/ч) – скорость сближения.
Продолжаем рассуждение.
Чтобы найти скорость второго пешехода, нужно из скорости сближения вычесть скорость первого пешехода.
2) 9 – 4 = 5 (км/ч)
Записываем ответ.
Ответ: 5 км/ч скорость второго пешехода.
Номер 63.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Вычисляем устно первую пару примеров.
600 : 3 + 7 ∙ 5 = 200 + 35 = 235
600 : (3 + 7) ∙ 5 = 600 : 10 ∙ 5 = 60 ∙ 5 = 300
Вычисляем устно вторую пару примеров.
40 ∙ (16 – 8) ∙ 2 = 40 ∙ 8 ∙ 2 = 320 ∙ 2 = 640
40 ∙ (16 – 8 ∙ 2) = 40 ∙ (16 – 16) = 40 ∙ 0 = 0
Номер 64.
Ответ:
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполняем вычисления с пояснениями.

Выполняем действия в выражении 8 070 ∙ 600 по алгоритму умножения трёхзначного числа на однозначное, не обращая внимания на нули, а затем приписываем в произведении то количество нулей, которое было в конце множителей.

Оформляем задание в тетрадь.
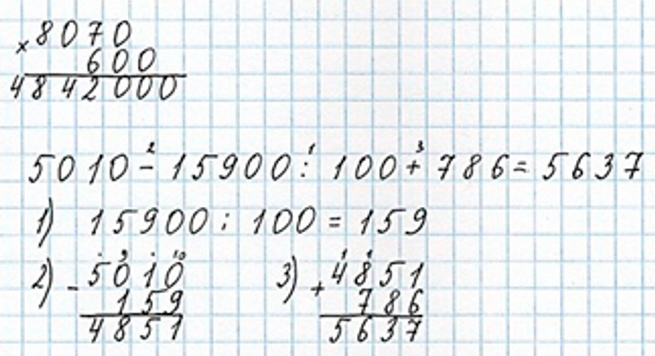
Задание внизу страницы
Ответ:
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполняем вычисления по действиям.
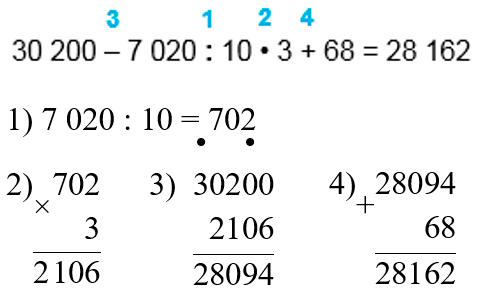
Оставшийся пример выполняем самостоятельно.
Выполняем вычисления и оформляем задание в тетрадь.
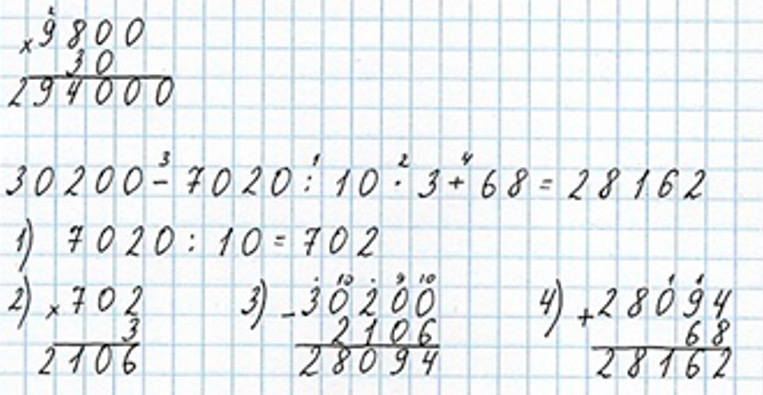
Задание на полях страницы
Цепочка.

24 ∙ 20 = 480 480 − 180 = 300 300 : 5 = 60 60 ∙ 80 = 4800 4800 : 10 = 480 480 ∙ 5 = 2400
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполняем вычисления, используя цепочку на полях страницы.
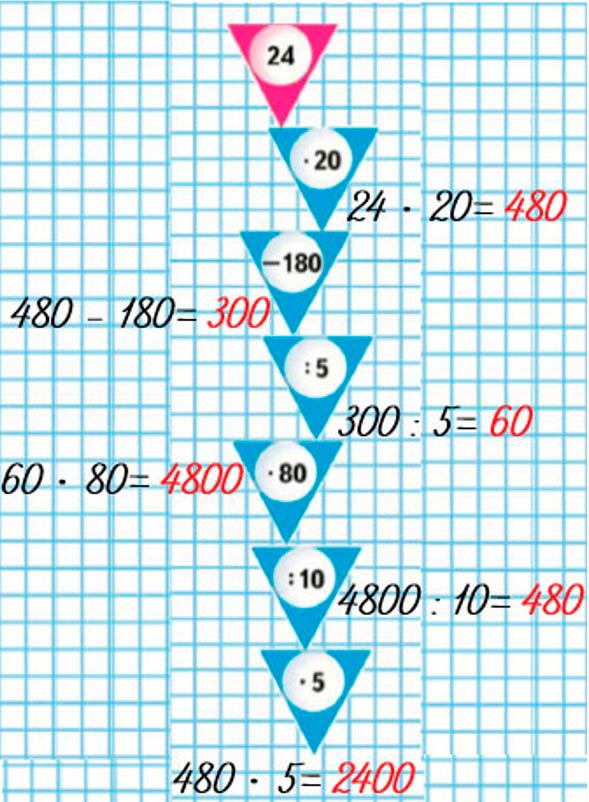
Оформляем задание в тетрадь.
24 ∙ 20 = 480
480 − 180 = 300
300 : 5 = 60
60 ∙ 80 = 4800
4800 : 10 = 480
480 ∙ 5 = 2400
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.