Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 15

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Задание вверху страницы
Сколько всего единиц в 42 дес.? в 420 дес.? в 35 сот.?
Объясни решение.
1 дес. = 10 ед.; 1 сот. = 100 ед.
42 дес. = 420 ед.
420 дес. = 4200 ед.
35 сот. = 3500 ед.
1) 80 ∙ 40 = 8 дес. ∙ (4 ∙ 10) = 8 дес. ∙ 4 ∙ 10 = 320 дес. = 3200
Так как 1 дес. = 10 ед., то 80 ед. = 8 дес., значит,
8 дес. ∙ 4 ∙ 10 = 320 дес. = 3200 ед.
2) 600 ∙ 90 = 6 сот. ∙ (9 ∙ 10) = 540 сот. = 54000 ед.
Так как 1 сот. = 100 ед., то 600 ед. = 6 сот., значит,
6 сот. ∙ 9 ∙ 10 = 540 сот. = 54000 ед.
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Объясним, сколько единиц в данных значениях.
1 дес. = 10 ед.; 1 сот. = 100 ед.
42 дес. = 420 ед.
420 дес. = 4200 ед.
35 сот. = 3500 ед.
Объясним решение первого примера.
1) 80 ∙ 40 = 8 дес. ∙ (4 ∙ 10) = 8 дес. ∙ 4 ∙ 10 = 320 дес. = 3200
Так как 1 дес. = 10 ед., то 80 ед. = 8 дес., значит,
8 дес. ∙ 4 ∙ 10 = 320 дес. = 3200 ед.
Объясним решение второго примера.
2) 600 ∙ 90 = 6 сот. ∙ (9 ∙ 10) = 540 сот. = 54000 ед.
Так как 1 сот. = 100 ед., то 600 ед. = 6 сот., значит,
6 сот. ∙ 9 ∙ 10 = 540 сот. = 54000 ед.
Номер 54.
Ответ:
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Выполняем вычисления первого примера с пояснением.
Выполняем действия по алгоритму умножения трёхзначного или многозначного числа на однозначное, не обращая внимания на нули, а затем приписываем в произведении то количество нулей, которое было в конце множителей.
Пишу: 4 200 ∙ 90.
4 200 ∙ 90 – это 42 сот., которые умножили на 9 дес., поэтому умножим 42 на 9, затем дописываем к произведению справа три нуля.
Умножаю единицы: 2 ∙ 9 = 18. 18 ед. – это 1 дес. и 8 ед., 8 ед. пишу под единицами, а 1 дес. запомню и прибавлю к десяткам после умножения десятков.
Умножаю десятки: 4 ∙ 9 = 36. К 36 дес. прибавляю 1 дес., который получен при умножении единиц: 36 + 1 = 37. 37 дес. – это 3 сот. и 7 дес., 7 дес. пишу под десятками, а 3 сот. в ответ в разряд сотен, так как других сотен для умножения нет.
Дописываю к произведению справа 3 нуля.
Читаю ответ: 378 000.
Далее рассуждаем аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
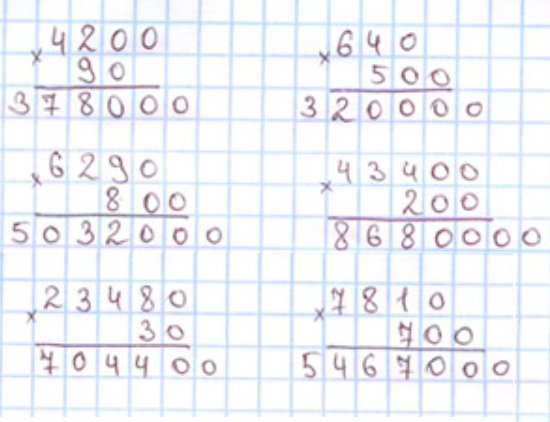
Номер 55.
Ответ:
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Выполняем вычисления по действиям.

Оставшиеся примеры решаем самостоятельно.
Выполняем вычисления и оформляем задание в тетрадь.

Номер 56.
От двух пристаней отправились навстречу друг другу два теплохода. Один из них шёл до встречи 4 ч со скоростью 36 км/ч. Другой теплоход прошёл до встречи третью часть пути, пройденного первым. Задай вопрос и реши задачу.
Ответ:Какое расстояние между двумя пристанями?

Можно оформить с помощью чертежа:

S = V ∙ t: Чтобы найти расстояние, надо скорость умножить на время.
V = S : t: Чтобы найти скорость, надо расстояние разделить на время.
t = S : V: Чтобы найти время, надо расстояние разделить на скорость.
Ставим вопрос к задаче.
Какое расстояние между двумя пристанями?
Оформляем условие в виде таблицы или схематического чертежа.

или
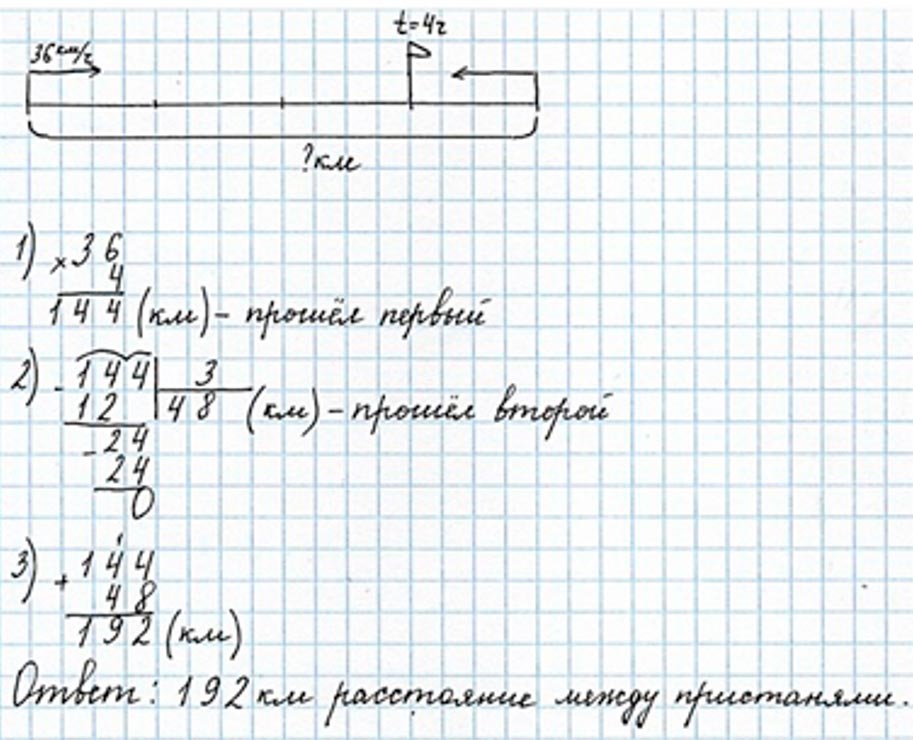
Рассуждаем.
Узнаем, сколько километров прошел первый теплоход. Для этого скорость умножаем на время в пути.
1) 36 ∙ 4 = 144 (км) – прошел первый теплоход.
Продолжаем рассуждение.
Узнаем, сколько километров прошел второй теплоход. Нам известно, что путь второго теплохода – это третья часть пути первого. Делим расстояние, которое прошел первый теплоход на 3.
2) 144 : 3 = 48 (км) – прошел второй теплоход
Продолжаем рассуждение.
Чтобы узнать, какое расстояние между пристанями, нужно сложить расстояния, которые преодолели оба теплохода.
3) 144 + 48 = 192 (км)
Записываем ответ.
Ответ: 192 км расстояние между пристанями.
Оформляем задание в тетрадь.

Номер 57.
Ваня и Коля пошли в школу в 8 ч 30 мин. У школы они встретились. Ваня шёл до встречи с Колей 12 мин. Сколько минут был в пути Коля?
Ответ:Коля был в пути столько же минут, сколько и Ваня – 12 минут. Возможен иной вариант, что Коля мог прийти к школе раньше и ждать друга. Ответ: Коля был в пути 12 минут.
Помни о соотношении числовых значений единиц измерения времени:
1 мин = 60 сек
1 час – 60 мин
1 сут = 24 часа
Оформляем условие в виде схематического чертежа.

Рассуждаем.
Ваня и Коля вышли из дома одновременно и до школы дошли тоже в одно и то же время. Значит на путь до школы и у Вани, и у Коли ушло одинаковое количество минут – 12 минут.
Записываем ответ.
Коля был в пути столько же минут, сколько и Ваня – 12 минут.
Номер 58.
Бабушке вместе с внучкой Олей 63 года, а вместе с внучкой Машей 65 лет. Всем им вместе 73 года. Сколько лет каждой из них?
Ответ:
1) 73 − 63 = 10 (л.) – Маше.

2) 73 − 65 = 8 (л.) – Оле.
3) 73 − 10 − 8 = 55 (л.) – бабушке.
Ответ: Маше – 10 л., Оле – 8 лет, бабушке – 55 лет.
Оформляем условие задачи в виде схематического чертежа.
Оформляем условие.

Рассуждаем.
Чтобы узнать возраст Маши, нужно из общего возраста вычесть возраст бабушки вместе с внучкой Олей.
1) 73 − 63 = 10 (л.) – Маше.
Продолжаем рассуждение.
Чтобы узнать возраст Оли, нужно из общего возраста вычесть возраст бабушки вместе с внучкой Машей.
2) 73 − 65 = 8 (л.) – Оле.
Продолжаем рассуждение.
Чтобы узнать возраст бабушки, нужно из общего возраста вычесть возраст внучек.
3) 73 − 10 − 8 = 55 (л.) – бабушке.
Записываем ответ.
Ответ: Маше – 10 л., Оле – 8 лет, бабушке – 55 лет.
Номер 59.
Запиши и реши уравнение:
1) Произведение неизвестного числа и числа 9 равно разности чисел 120 и 66. 2) Частное неизвестного числа и числа 8 равно сумме чисел 320 и 80.
Ответ:
1) х ∙ 9 = 120 − 66
х ∙ 9 = 54
х = 54 : 9
х = 6
6 ∙ 9 = 120 − 66
54 = 54
Ответ: х = 6.
2) х : 8 = 320 + 80
х : 8 = 400
х = 400 ∙ 8
х = 3200
3200 : 8 = 320 + 80
400 = 400
Ответ: х = 3200.
Уравнение – равенство с неизвестной, при подстановке числа в которую, получается верное равенство.
Вспомни названия компонентов действия умножения, и зависимость между компонентами и результатом действия умножения:
1 множитель ∙ 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Уменьшаемое – вычитаемое = значение разности.
Уменьшаемое – значение разности = вычитаемое.
Значение разности + вычитаемое = уменьшаемое.
Делимое : делитель = значение разности.
Делимое : значение разности = делитель.
Значение разности ∙ делитель = делимое
Запишем и решим первое уравнение.
х ∙ 9 = 120 − 66
х ∙ 9 = 54
х = 54 : 9
х = 6
Проверка:
6 ∙ 9 = 120 − 66
54 = 54
Ответ: х = 6.
Запишем и решим второе уравнение.
х : 8 = 320 + 80
х : 8 = 400
х = 400 ∙ 8
х = 3200
Проверка:
3200 : 8 = 320 + 80
400 = 400
Ответ: х = 3200.
Номер 60.
Заполни пропуски.
Ответ:
8 см2 25 мм2 = 825 мм2
9 дм2 18 см2 = 918 см2
1 м2 50 дм2 = 150 дм2
1 м2 50 см2 = 10050 см2
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм², см², дм², м², км² и др.
Помни о соотношении числовых значений единиц измерения площади:
1 см² = 100 мм²
1 дм² = 100 см²
1 м² = 10 000 см²
1 м² = 100 дм²
Выполняем вычисления.
8 см² 25 мм² = 825 мм²
9 дм² 18 см² = 918 см²
1 м² 50 дм² = 150 дм²
1 м² 50 см² = 10050 см²
Оформляем задание в тетрадь.
Задание внизу страницы
Ответ:
Чтобы найти произведение круглых чисел, надо выполнить умножение, не обращая внимания на нули на конце, а затем в полученном произведении приписать справа столько нулей, сколько их на конце обоих множителей вместе.
Алгоритм:
1) Пишу первый множитель.
2) Второй множитель записываю так, чтобы нули остались в стороне.
3) Правильно умножаю числа, не обращая внимания на нули.
4) Считаю нули и приписываю.
Выполняем вычисления с пояснениями.

Выполняем действия по алгоритму табличного умножения, не обращая внимания на нули, а затем приписываем в произведении то количество нулей, которое было в конце множителей.
Пишу: 5 000 ∙ 30.
5 000 ∙ 30 – это 5 тыс., которые умножили на 3 дес., поэтому умножим 5 на 3, затем допишем к произведению справа четыре нуля.
Умножаю единицы: 5 ∙ 3 = 15. 15 ед. – это 1 дес. и 5 ед., 5 ед. пишу под единицами, а 1 дес. в ответ в разряд десятков, так как других десятков для умножения нет.
Допишем к произведению справа 4 нуля.
Читаю ответ: 150 000.
Далее рассуждаем аналогично.
Выполняем вычисления и оформляем задание в тетрадь.
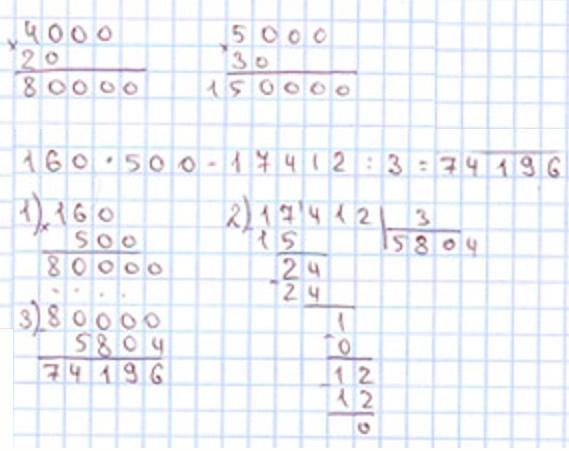
Задание на полях страницы
Цепочка.

Ответ:
36 ∙ 10 = 360 360 ∙ 100 = 36000 36000 : 9 = 4000 4000 − 50 = 3950 3950 : 10 = 395
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполняем вычисления, используя цепочку на полях.
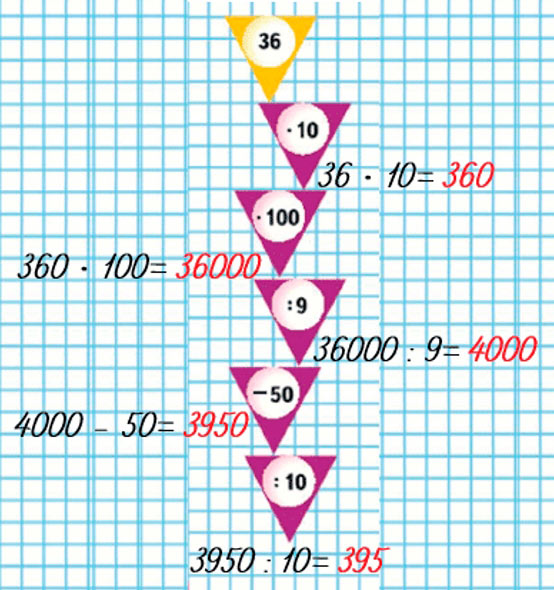
Оформляем задание в тетрадь.
36 ∙ 10 = 360
360 ∙ 100 = 36000
36000 : 9 = 4000
4000 − 50 = 3950
3950 : 10 = 395
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.