Математика 4 класс учебник Моро, Бантова 2 часть ответы – страница 12
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Умножение на числа, оканчивающиеся нулями
Задание вверху страницы
Объясни, как подсчитали разными способами, сколько всего рублей составляют эти монеты.
5 ∙ (4 ∙ 2) = в скобках записано количество монет в двух рядах, а затем это количество умножают на достоинство монет, находя сумму. (5 ∙ 4) ∙ 2 = в скобках находят сумму всех монет в одном ряду, а затем умножают на два, потому что ряда 2. (5 ∙ 2) ∙ 4 = в скобках действием находим сумму в паре двух монеток одинаковым достоинством, а затем полученное значение умножаем на 4, потому что таких пар можно составить 4.
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Рассмотрим изображение и записи, которые к ним относятся.
5 ∙ (4 ∙ 2) = 40
(5 ∙ 4) ∙ 2 = 40
(5 ∙ 2) ∙ 4 = 40
Объясним различные способы умножения.
5 ∙ (4 ∙ 2) = в скобках записано количество монет в двух рядах, а затем это количество умножают на достоинство монет, находя сумму.
(5 ∙ 4) ∙ 2 = в скобках находят сумму всех монет в одном ряду, а затем умножают на два, потому что ряда 2.
(5 ∙ 2) ∙ 4 = в скобках действием находим сумму в паре двух монеток одинаковым достоинством, а затем полученное значение умножаем на 4, потому что таких пар можно составить 4.
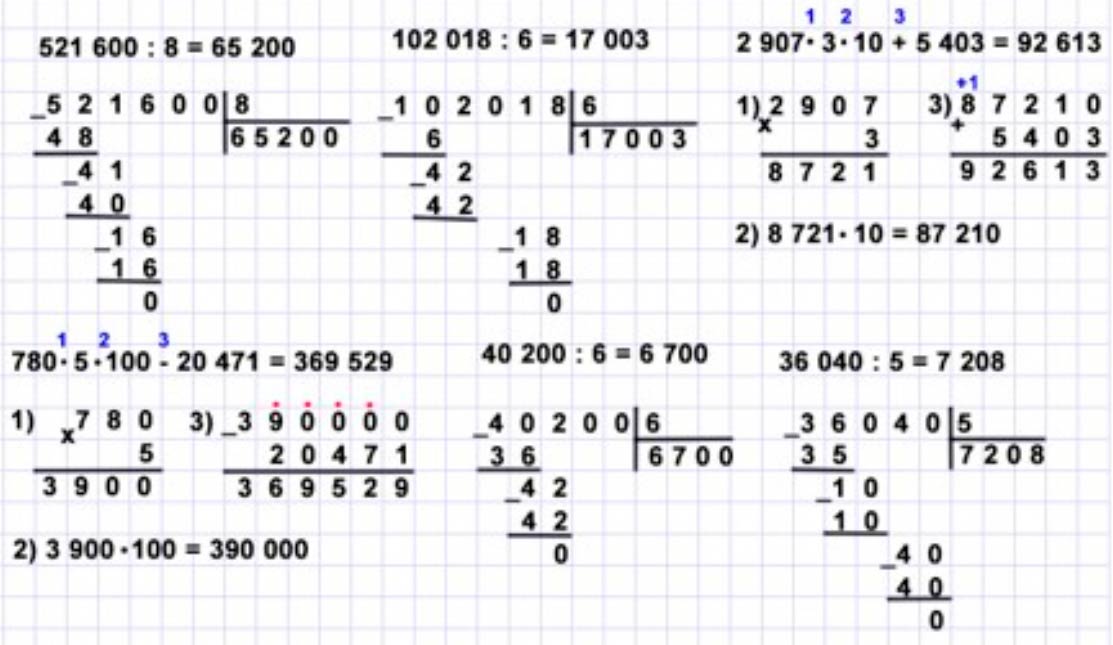
Номер 35.
Вычисли. Сравни способы вычислений и результаты.
Ответ:
7 ∙ (2 ∙ 5) = 7 ∙ 10 = 70
7 ∙ (2 ∙ 5) = (7 ∙ 2) ∙ 5 = 70
7 ∙ (2 ∙ 5) = (7 ∙ 5) ∙ 2 = 70
Первый пример решался по правилу: первое действие в скобках, а за тем все остальные.
Во втором примере было использовано сочетательное свойство умножения: a ∙ (b ∙ c) = (a ∙ b) ∙ c.
Главное, что говорит сочетальльное свойство умножения - меняя позиции множителей и расставляя скобки значение примера не изменится.
4 ∙ (5 ∙ 3) = 4 ∙ 15 = 60
4 ∙ (5 ∙ 3) = (4 ∙ 5) ∙ 3 = 60
4 ∙ (5 ∙ 3) = (4 ∙ 3) ∙ 5 = 60
Первый пример решался по правилу: первое действие в скобках, а за тем все остальные.
Во втором примере было использовано сочетательное свойство умножения: a ∙ (b ∙ c) = (a ∙ b) ∙ c.
Третий пример тоже решался с применением сочетального свойства умножения.
Главное, что говорит сочетальльное свойство умножения - меняя позиции множителей и расставляя скобки значение примера не изменится.
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполним вычисления и сравним способы и результаты вычислений первого столбика примеров.
7 ∙ (2 ∙ 5) = 7 ∙ 10 = 70
7 ∙ (2 ∙ 5) = (7 ∙ 2) ∙ 5 = 70
7 ∙ (2 ∙ 5) = (7 ∙ 5) ∙ 2 = 70
Первый пример решался по правилу: первое действие в скобках, а за тем все остальные.
Во втором примере было использовано сочетательное свойство умножения:
a ∙ (b ∙ c) = (a ∙ b) ∙ c.
Главное, что говорит сочетательное свойство умножения – меняя позиции множителей и расставляя скобки, значение примера не изменится.
Выполним вычисления и сравним способы и результаты вычислений второго столбика примеров.
4 ∙ (5 ∙ 3) = 4 ∙ 15 = 60
4 ∙ (5 ∙ 3) = (4 ∙ 5) ∙ 3 = 60
4 ∙ (5 ∙ 3) = (4 ∙ 3) ∙ 5 = 60
Первый пример решался по правилу: первое действие в скобках, а за тем все остальные.
Во втором примере было использовано сочетательное свойство умножения:
a ∙ (b ∙ c) = (a ∙ b) ∙ c.
Третий пример тоже решался с применением сочетательного свойства умножения.
Главное, что говорит сочетательное свойство умножения – меняя позиции множителей и расставляя скобки, значение примера не изменится.
Номер 36.
Вычисли результат удобным способом.
Ответ:12 ∙ (5 ∙ 7) = (12 ∙ 5) ∙ 7 = 60 ∙ 7 = 420 29 ∙ (2 ∙ 5) = 29 ∙ 10 = 290 35 ∙ (2 ∙ 7) = (35 ∙ 2) ∙ 7 = 70 ∙ 7 = 490 17 ∙ (4 ∙ 10) = (17 ∙ 4) ∙ 10 = 68 ∙ 10 = 680
Алгоритм записи и решения умножения на числа, оканчивающиеся нулями:
1) Записываем первый множитель.
2) Второй множитель записываем так, чтобы нули остались в стороне.
3) Умножаем многозначное число на число, не обращая внимания на нули.
4) К полученному результату приписываем эти нули.
5) Читаем ответ.
Выполним вычисления удобным способом.
12 ∙ (5 ∙ 7) = (12 ∙ 5) ∙ 7 = 60 ∙ 7 = 420
29 ∙ (2 ∙ 5) = 29 ∙ 10 = 290
35 ∙ (2 ∙ 7) = (35 ∙ 2) ∙ 7 = 70 ∙ 7 = 490
17 ∙ (4 ∙ 10) = (17 ∙ 4) ∙ 10 = 68 ∙ 10 = 680
Оформим задание в тетрадь.
Номер 37.
В хозяйстве от каждой коровы получали в среднем по 14 л молока в сутки. Сколько литров молока получат в этом хозяйстве от 10 коров за 7 суток? Реши задачу разными способами.
Ответ:
1 к. за 1 сут. – 14 л
10 к. за 7 сут. – ? л
Можно оформить так:
1) 14 ∙ 10 = 140 (л) – молока получат от 10 коров в сутки.
2) 140 ∙ 7 = 980 (л)
Ответ: 980 литров молока получат от 10 коров за 7 суток.
1) 14 ∙ 7 = 98 (л) – молока получат от одной коровы за 7 суток.
2) 98 ∙ 10 = 980 (л)
Ответ: 980 литров молока получат 10 коров за 7 суток.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
Шаг 2.
Рассуждаем.
Для начала узнаем, сколько молока получат от 10-ти коров в сутки.
1) 14 ∙ 10 = 140 (л) – молока получат от 10 коров в сутки.
Продолжаем рассуждение.
Чтобы узнать, сколько литров молока получат за 7 суток от 10-ти коров, нужно количество молока, получаемое в сутки умножить на 7.
2) 140 ∙ 7 = 980 (л)
Записываем ответ.
Ответ: 980 литров молока получат от 10 коров за 7 суток.
Шаг 1.
Рассуждаем.
Для начала узнаем, сколько молока получат от 1-й коровы за 7 суток.
1) 14 ∙ 7 = 98 (л) – молока получат от одной коровы за 7 суток.
Продолжаем рассуждение.
Чтобы узнать, сколько литров молока получат за 7 суток от 10-ти коров, нужно количество молока, получаемое в сутки от 1-й коровы умножить на 10.
2) 98 ∙ 10 = 980 (л)
Записываем ответ.
Ответ: 980 литров молока получат 10 коров за 7 суток.
В цветочном хозяйстве в каждом парнике ежедневно срезают по 28 роз. Сколько роз могут срезать в 10 парниках этого хозяйства за 5 дней, если количество срезанных в день роз не изменяется? Сколькими способами можно решить эту задачу?
Ответ:Задачу можно решить двумя способами.
1 парник за 1 сутки – 28 роз
10 парников за 5 дней – ?
Можно оформить так:
1) 28 · 10 = 280 (роз) – можно срезать в 10 парниках за сутки;
2) 280 · 5 = 1400 (роз) – можно срезать в 10 парниках за 5 дней.
Ответ: 1400 роз.
1) 28 · 5 = 140 (роз) – можно срезать в одном парнике за 5 дней;
2) 140 · 10 = 1400 (роз) – можно срезать в 10 парниках за 5 дней.
Ответ: 1400 роз.
Номер 38.
С поля вывозили овощи на 10 машинах. Каждая из этих машин делала по 8 рейсов в день и вывозила по 5 т овощей за один рейс. Сколько тонн овощей вывезли эти машины за 6 дней?
Ответ:
1) 10 ∙ 8 = 80 (р.) – количество рейсов сделали 10 машин за 1 день
2) 5 ∙ 80 = 400 (т) – вывезли овощей 10 машин за 1 день
3) 400 ∙ 6 = 4 сот. ∙ 6 = 24 сот. = 2 400 (т) – вывезли овощей за 6 дней
Ответ: 2400 т.
1) 5 ∙ 8 = 40 (т) – 1 машина за 1 день.
2) 40 ∙ 10 = 400 (т) – 10 машин за 1 день.
3) 400 ∙ 6 = 2400 (т)
Ответ: 2400 т вывезли эти машины.
1) 5 ∙ 10 = 50 (т) – вывезло овощей 10 машин за 1 рейс
2) 50 ∙ 8 = 400 (т) – вывезли овощей 10 машин за 8 рейсов
3) 400 ∙ 6 = 4 сот. ∙ 6 = 24 сот. = 2 400 (т) – вывезли овощей за 6 дней
Ответ: 2400 т.
1) 6 ∙ 8 = 48 (рейсов) – количество рейсов сделает 1 машина за 6 дней
2) 48 ∙ 10 = 480 (рейсов) – количество рейсов сделают 10 машин за 6 дней
3) 480 ∙ 5 = 2 400 (т) – вывезли овощей за 6 дней
Ответ: 2400 т.
Оформляем условие задачи в виде таблицы.
Оформляем условие.
Рассуждаем.
Узнаем, сколько рейсов делают 10 машин за 1 день.
1) 10 ∙ 8 = 80 (р.) – сделали 10 м. за 1 день.
Продолжаем рассуждение.
Чтобы узнать, сколько овощей вывезли за день 10 машин, нужно грузоподъемность одной машины умножить на количество рейсов за день.
2) 5 ∙ 80 = 400 (т) – овощей вывезли за 1 день 10 м.
Продолжаем рассуждение.
Чтобы узнать, сколько овощей вывезли эти машины за 6 дней, нужно количество овощей вывозимых за один день умножить на 6.
3) 400 ∙ 6 = 2400 (т) – овощей, вывезли за 6 д.
Записываем ответ.
Ответ: 2400 т вывезли эти машины.
Номер 39.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления по действиям.
Самостоятельно выполняем оставшиеся примеры.
Оформляем задание в тетрадь.
Задание внизу страницы
Ответ:9 ∙ (4 ∙ 25) = 9 ∙ 100 = 900 15 ∙ (4 ∙ 9) = (15 ∙ 4) ∙ 9 = 60 ∙ 9 = 540 11 ∙ (10 ∙ 3) = 11 ∙ 30 = 330 10 ∙ (29 ∙ 2) = 10 ∙ 58 = 580
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем и выполняем вычисления.
Группируем множители так, чтобы последним действием умножать на круглое число.
9 ∙ (4 ∙ 25) = 9 ∙ 100 = 900
15 ∙ (4 ∙ 9) = (15 ∙ 4) ∙ 9 = 60 ∙ 9 = 540
11 ∙ (10 ∙ 3) = 11 ∙ 30 = 330
10 ∙ (29 ∙ 2) = 10 ∙ 58 = 580
Оформляем задание в тетрадь.
9 ∙ (4 ∙ 25) = 9 ∙ 100 = 900
15 ∙ (4 ∙ 9) = (15 ∙ 4) ∙ 9 = 60 ∙ 9 = 540
11 ∙ (10 ∙ 3) = 11 ∙ 30 = 330
10 ∙ (29 ∙ 2) = 10 ∙ 58 = 580
Задание на полях страницы
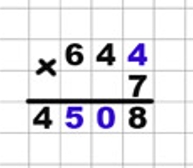
Ребус.
Перед нами ребус, для того чтобы найти недостающие цифры необходимо выполнить умножение.
Рассмотрим ребус.
Разгадаем ребус.
Какое число надо умножить на 7, чтобы в единицах получилось 8? Это число 4.
4 ∙ 7 = 28, да еще 2 дес., которые получились при умножении единиц:
28 + 2 = 30. Пишу 0 под десятками.
6 ∙ 7 = 42, да еще 3 сот., которые получились при умножении десятков:
42 + 3 = 45. Пишу 5 под сотнями.
Оформим задание в тетрадь.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.