Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 93

Учебник 1 часть. Математика 4 класс. Учебник Моро.

Тип: ГДЗ, Решебник.
Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
Часть: 1.
Год: 2020-2024.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Ольга Дмитриева

математика 4 класс Моро, Бантова - 1 часть страница 93

Номер 23.

В соревнованиях по ориентированию на местности участвовало 86 школьников. Победителями стали 5 человек, а две третьих всех остальных ребят за хорошие результаты были награждены грамотами. Сколько ребят получили грамоты?

Ответ:

Оформим или с помощью чертежа, или с помощью краткой записи:

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 23

1) 86 − 5 = 81 (шк.) – не были победителями. 2) 81 : 3 = 27 (шк.) – 1 часть. 3) 27 ∙ 2 = 54 (шк.) – школьника всего
Ответ: 54 школьника получили грамоты.

Подсказка:

Доля – одна часть из тех, на которые разделили целое. Например, если целое разделили на 4 части, то доля – это одна четвертая, т.е. одна часть из четырех
Одна вторая – половина целого
Одна третья – третья часть от целого
Одна четвертая – четвертинка или четвертая часть от целого
Одна пятая – пятая часть от целого и т.д.
Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.

Шаг 1.
Оформляем условие в виде схематического чертежа или краткой записи.

Шаг 2.
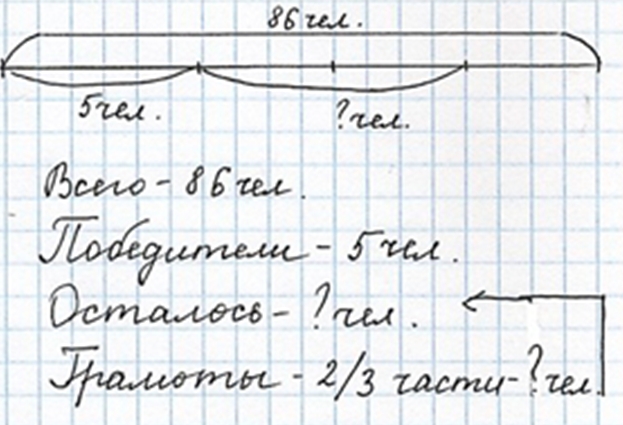
Рассуждаем.

Чтобы узнать, сколько человек не победили, вычитаем из общего количества человек количество победивших.
1) 86 − 5 = 81 (шк.) – не были победителями.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, сколько ребят получили грамоты, нужно общее количество человек разделить на 3 части, а взять из них одну.
2) 81 : 3 = 27 (шк.) – 1 часть.
3) 27 ∙ 2 = 54 (шк.)

Шаг 4.
Записываем ответ.

Ответ: 54 школьника получили грамоты.

Номер 24.

1) Запиши равенство и проверь, верно ли оно: частное чисел 72180 и 9 равно разности чисел 90000 и 81980. 2) Запиши неравенство и проверь, верно ли оно: произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174.

Ответ:

1) 72180 : 9 = 90000 – 81980 верно.

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 24

8020 = 8020
2) 4070 ∙ 8 < 18396 + 14174 верно.

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 24-1

32560 < 32570

Подсказка:

Помни о том, что является признаками равенства и неравенства:
Равенство – это выражение, составленное из чисел, знаком арифметических действий, скобок и знака равно, т.о.

   – числа
   – знаки арифметических действий
   – скобки
   – знак равно

Неравенство – выражение, составленное из чисел, знаков арифметических действий, скобок и знаков больше/меньше.

   – числа
   – знаки арифметических действий
   – скобки
   – знаки больше или меньше

Чтобы доказать, верно равенство и неравенство или нет, нужно вычислить значения выражений обеих частей.

Шаг 1.
Запишем равенство и проверим, верно ли оно:

72180 : 9 = 90000 − 81980 верно.

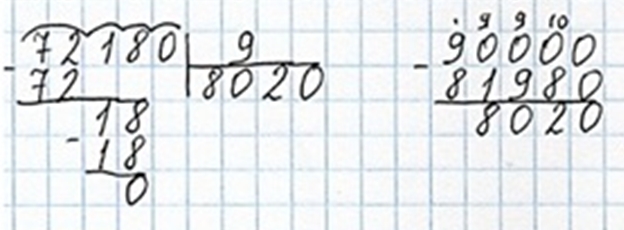
8020 = 8020

Шаг 2.
Запишем неравенство и проверим, верно ли оно:

4070 ∙ 8 < 18396 + 14174 верно.

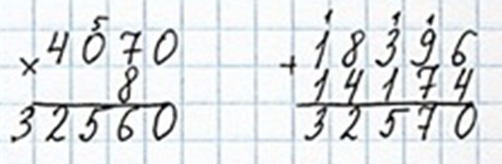
32560 < 32570

Шаг 3.
Оформим задание в тетрадь.

Номер 25.

Длины сторон треугольника равны 12 см 5 мм, 4 см, 10 см 5 мм. Вырази длины сторон в миллиметрах и найди периметр этого треугольника.

Ответ:

12 см 5 мм = 125 мм 4 см = 40 мм 10 см 5 мм = 105 мм 125 + 40 + 105 = 270 мм
Ответ: 270 мм периметр треугольника.

Подсказка:

Длина – величина, характеризующая протяженность объекта на плоскости, выражается в таких единицах измерения, как миллиметр, сантиметр, дециметр, метр, километр.
Помни о соотношении числовых значений единиц измерения длины:

   1 см = 10 мм
   1 дм = 10 см
   1 м = 100 см
   1 м = 10 дм
   1 км = 1000 м

Ломаная – геометрическая фигура, составленная из отрезков звеньев. Длина ломаной – сумма длин всех отрезков звеньев. Чтобы вычислить длину ломаной, нужно измерить длины всех звеньев, а полученные значения сложить. Вычисляется сложением. В независимости от того, замкнутая ломаная или нет, ее длина всегда вычисляется одинаково.
Треугольник – замкнутая ломаная

Шаг 1.
Рассуждаем и выполняем вычисление.

Треугольник – замкнутая ломаная. Периметр треугольник – сумма длин всех его сторон. Чтобы вычислить периметр треугольника, нужно измерить длины всех сторон, а полученные значения сложить.

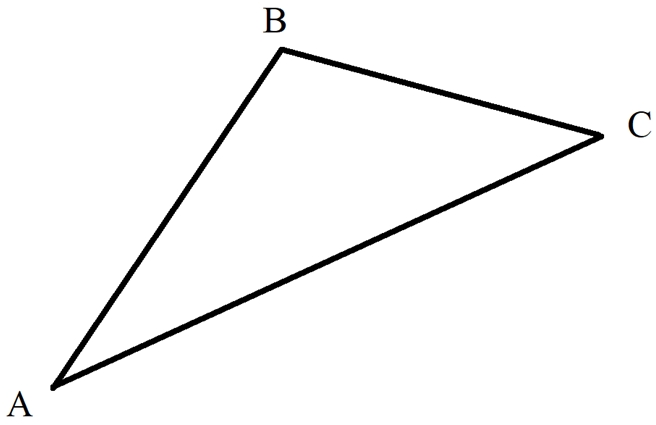
АВС – треугольник
АВ = 10 см 5 мм = 105 мм
ВС = 4 см = 40 мм
АС = 12 см = 120 мм
Р = ? см
Р = АВ + ВС + АС
Р = 105 мм + 40 мм + 120 мм = 270 мм

Шаг 2.
Оформим задание в тетрадь.

12 см 5 мм = 125 мм
4 см = 40 мм
10 см 5 мм = 105 мм
125 + 40 + 105 = 270 мм
Ответ: 270 мм периметр треугольника.

Номер 26.

Начерти тупой, прямой и острый углы с общей стороной.

Ответ:

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 26

Подсказка:

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Все углы согласно градусной мере делятся на несколько групп:
Прямой угол – угол, градусная мера которого равна 90 градусам.
Острый угол – угол, меньше прямого угла
Тупой угол – угол, больше прямого и меньше развернутого.

Шаг 1.
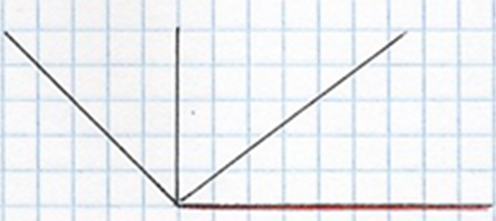
Начертим тупой, прямой и острый углы с общей стороной.

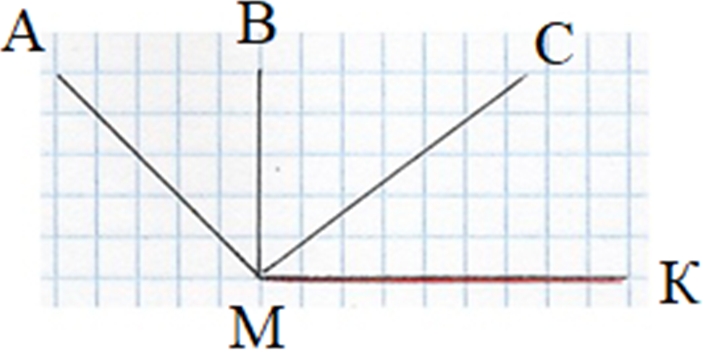
СМК – острый угол
ВМК – прямой угол
АМК – тупой угол

Шаг 2.
Оформим задание в тетрадь.

Номер 27.

В дом отдыха приехали 70 женщин и 50 мужчин. Сколько столов они заняли в столовой, если за каждый стол сели по 4 человека?

Ответ:

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 27

1) 70 + 50 = 120 (чел.) – было в доме отдыха. 2) 120 : 4 = 30 (ст.) – было занято всего
Ответ: 30 столов было занято.

Подсказка:

Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:

   1 множитель ∙ 2 множитель = значение произведения.
   Значение произведения : 1 множитель = 2 множитель.
   Значение произведения : 2 множитель = 1 множитель.

Данная задача: вида «количество человек за 1 столом, количество столов, общее количество человек» характеризуется зависимостями между компонентами:

   Кол-во человек за 1 столов ∙ кол-во столов = общее кол-во человек.
   Общее кол-во человек : кол-во столов = кол-во человек за 1 столов.
   Общее кол-во человек : кол-во человек за 1 столом = кол-во столов.

Шаг 1.
Оформляем условие в виде таблицы.

Шаг 2.
Рассуждаем.

Чтобы узнать, сколько всего людей приехало, складываем количество мужчин и женщин.
1) 70 + 50 = 120 (чел.) – было в доме отдыха.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, сколько столов потребовалось, нужно общее количество человек разделить на количество человек за 1 столом.
2) 120 : 4 = 30 (ст.)

Шаг 4.
Записываем ответ.

Ответ: 30 столов было занято.
Решение выражением: (70 + 50) : 4, где 70 + 50 – общее количество человек в доме отдыха, а 4 – количество человек за 1 столом.

Номер 28.

Найди:

1) площадь прямоугольника DEKM; 2) площадь и периметр треугольников DEK и DKM.

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 28

Ответ:

1) 10 ∙ 26 = 260 (мм²) – площадь прямоугольника DEKM. 2) 260 : 2 = 130 (мм²) – площадь треугольников DEK и DKM. 3) 26 + 28 + 10 = 64 (мм) – периметр треугольников DEK и DKM.
Ответ: площадь прямоугольника DEKM составляет 260 мм², площадь треугольников DEK и DKM составляет 130 мм², периметр треугольников DEK и DKM составляет 64 мм.

Подсказка:

Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм², см², дм², м², км² и др.
Помни о соотношении числовых значений единиц измерения площади:

   1 см² = 100 мм²
   1 дм² = 100 см²
   1 м² = 10 000 см²
   1 м² = 100 дм²

Площадь прямоугольника – произведение длин его сторон. Чтобы вычислить площадь прямоугольника, нужно измерить длины его сторон, а полученные значения перемножить. Вычисляется умножением.
Ломаная – геометрическая фигура, составленная из отрезков звеньев. Длина ломаной – сумма длин всех отрезков звеньев. Чтобы вычислить длину ломаной, нужно измерить длины всех звеньев, а полученные значения сложить. Вычисляется сложением. В независимости от того, замкнутая ломаная или нет, ее длина всегда вычисляется одинаково.
Треугольник – замкнутая ломаная

Шаг 1.
Рассмотрим треугольник на полях страницы.

Шаг 2.
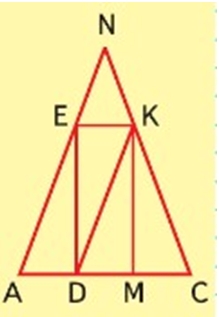
Найдем площадь прямоугольника DEKM.

DEKM – прямоугольник
DE = MK = 1 см
DM = EK = 2 см 6 мм
S = DE ∙ EK
S = ? мм²
S = 1 см ∙ 2 см 6 мм = 10 мм ∙ 26 мм = 260 мм² – площадь прямоугольника

Шаг 3.
Найдем площадь и периметр треугольников DEK и DKM.

DEK – треугольник
Площадь треугольника по формуле мы еще вычислять не умеем, но площадь этого треугольника равна половине площади прямоугольника DEKM, значит, 260 мм² : 2 = 130 мм² – площадь треугольника
Периметр – сумма длин всех сторон фигуры. Значит, чтобы узнать, чему равен периметр треугольника, нужно измерить длины всех его сторон, а полученные значения сложить. При этом треугольники DEK и DKM равны, значит, что и периметры этих фигур равны.
DE = 2 см 6 мм
ЕК = 1 см
KD = 2 см 8 мм
P = ? см
P = EK + KD + ED
P = 2 см 6 мм + 1 см + 2 см 8 мм = 6 см 4 мм = 64 мм

Шаг 4.
Оформим задание в тетрадь.

Номер 29.

В трёх корзинах 96 кг слив. В первой корзине 28 кг, во второй — третья часть всех слив. Сколько килограммов слив в третьей корзине?

Ответ:

математика 4 класс Моро, Бантова - 1 часть страница 93, номер 29

1-й способ решения:

1) 96 : 3 = 32 (кг) – слив во второй корзине. 2) 28 + 32 = 60 (кг) – слив в первой и второй корзине. 3) 96 – 60 = 36 (кг) – слив в третьей корзине
Ответ: 36 кг слив в третьей корзине.

2-й способ решения:

1) 96 : 3 = 32 (кг) – во второй корзине 2) 96 – 32 = 64 (кг) – в первой и третьей корзине вместе 3) 64 – 28 = 36 (кг) – в третьей корзине
Ответ: 36 кг слив.

Подсказка:

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
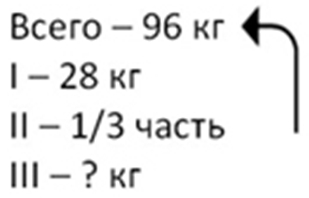
Рассуждаем.

Чтобы узнать, сколько слив во второй корзине, нужно общее количество слив разделить на 3, а взять только одну часть.
1) 96 : 3 = 32 (кг) – слив во второй корзине.

Шаг 3.
Продолжаем рассуждение.

Чтобы узнать, сколько слив в первой и второй корзинах вместе, складываем количество слив каждой корзины.
2) 28 + 32 = 60 (кг) – слив в первой и второй корзине.

Шаг 4.
Продолжаем рассуждение.

Чтобы узнать, сколько слив в третьей корзине, нужно из общего количества слив вычесть количество слив первой и второй корзины.
3) 96 − 60 = 36 (кг)

Шаг 5.
Записываем ответ.

Ответ: 36 кг слив в третьей корзине.

Номер 30.

Периметр квадрата равен 36 см. Найди его площадь.

Ответ:

1) 36 : 4 = 9 (см) – сторона квадрата. 2) 9 ∙ 9 = 81 (см²) – площадь квадрата.
Ответ: площадь квадрата составляет 81 см².

Подсказка:

Ломаная – геометрическая фигура, составленная из отрезков звеньев. Длина ломаной – сумма длин всех отрезков звеньев. Чтобы вычислить длину ломаной, нужно измерить длины всех звеньев, а полученные значения сложить. Вычисляется сложением. В независимости от того, замкнутая ломаная или нет, ее длина всегда вычисляется одинаково.
Квадрат – замкнутая ломаная
Площадь – величина, которая характеризует размер части плоскости, занятой фигурой. Измеряется в таких единицах измерения, как: мм², см², дм², м², км² и др.
Помни о соотношении числовых значений единиц измерения площади:

   1 см² = 100 мм²
   1 дм² = 100 см²
   1 м² = 10 000 см²
   1 м² = 100 дм²

Шаг 1.
Начертим квадрат и найдем его площадь.

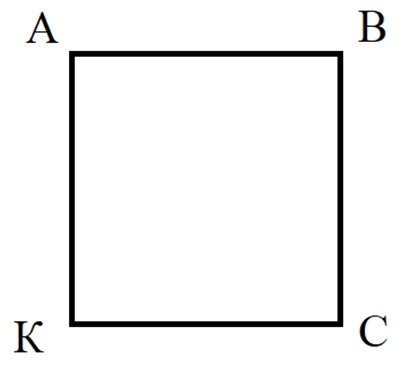
АВСК – квадрат
P = AB + BC + CK + АК
Но квадрат – прямоугольник, у которого все стороны равны, значит, сложение одинаковых слагаемых можно заменить умножением. Тогда периметр квадрата равен а ∙ 4
Значит, а ∙ 4 = 36, а = 36 : 4 = 9 см
Мы узнали, что сторона квадрата равна 9 см.
Площадь квадрата это произведение длин его сторон. А раз длина стороны квадрата одинаковая, то площадь квадрата равна а ∙ а.
Значит, а ∙ а = 9 ∙ 9 = 81 см ²

Шаг 2.
Оформим задание в тетрадь.

Номер 31.

Ответ:

Подсказка:

Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.

Помни о том, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:

1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном.
3) Нахожу, сколько сотен разделили.
4) Нахожу, сколько сотен осталось разделить.
5) Образую второе неполное делимое.
6) Нахожу, количество десятков в частном.
7) Нахожу, сколько десятков разделили.
8) Нахожу, сколько десятков осталось разделить.
9) Образую третье неполное делимое.
10) Нахожу количество единиц в частном.
11) Нахожу, сколько единиц разделили.
12) Нахожу, сколько единиц осталось разделить.
13) Читаю ответ.

Помни о том, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:

1) Записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить.
2) Записываю второй множитель так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Умножение начинаю с единиц низшего разряда.
5) Умножаю десятки.
6) Умножаю сотни.
7) Умножение окончено. Читаю ответ.

Следуй плану при устном объяснении вычитания в столбик:

1) Записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус.
2) Записываю вычитаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Вычитание начинаю с единиц низшего разряда. Вычитаю единицы.
5) Вычитаю десятки.
6) Ввычитаю сотни.
7) Вычитание окончено. Читаю ответ.

Шаг 1.
Выполняем вычисления по действиям.

5 000 : 100 + 499 = 549
1) 5 000 : 100 = 50

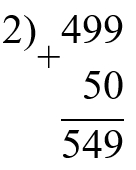
(50 100 − 100) : 100 = 500
1) 50 100 − 100 = 50 000
2) 50 000 : 100 = 500

900 - (600 - 130 ∙ 4) : 10 = 892

3) 80 : 10 = 8

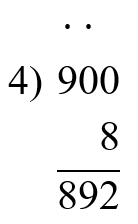
800 − 250 + 130 : 5 ∙ 2 = 602

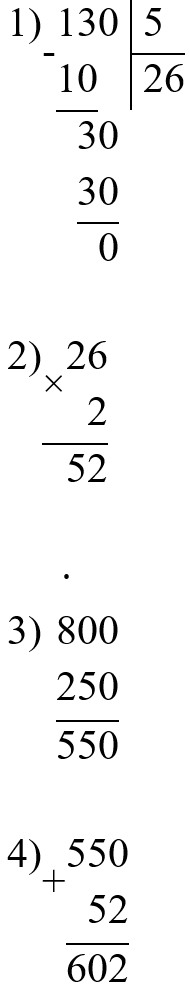
900 − 348 : 4 ∙ 6 = 378

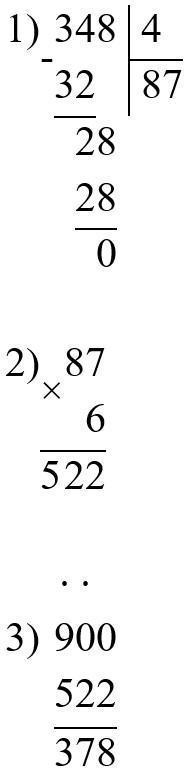
696 − 612 : 6 : 3 = 662

Шаг 2.
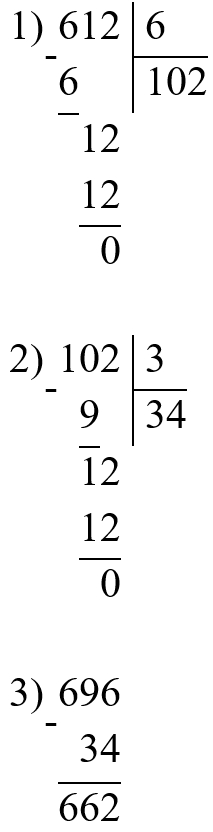
Оформляем задание в тетрадь.

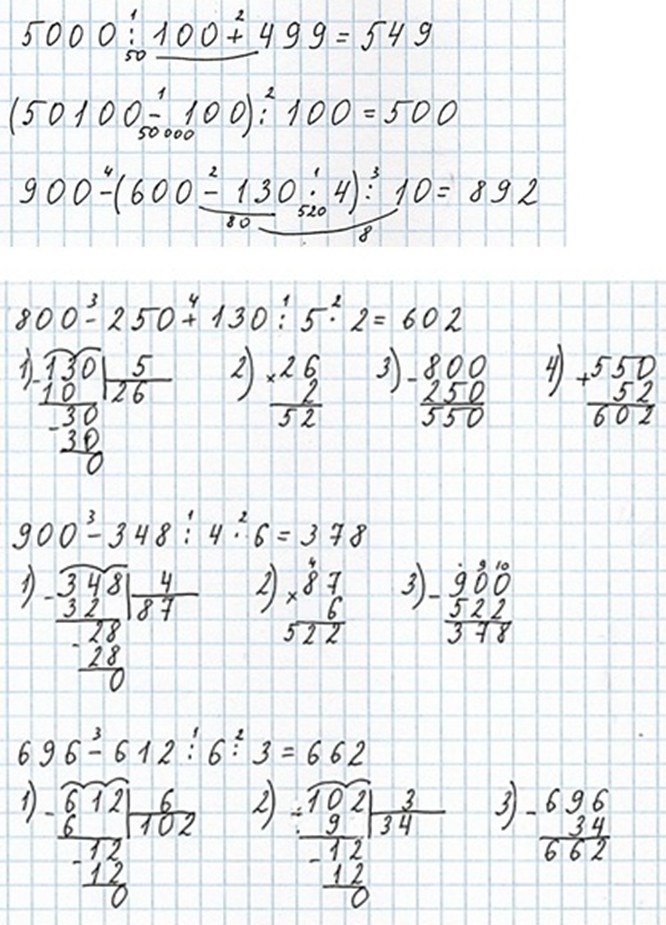
Номер 32.

Запиши и прочитай наименьшее семизначное и наибольшее пятизначное числа.

Ответ:

Наименьшее семизначное число – 1000000 – один миллион. Наибольшее пятизначное число – 99999 – девяносто девять тысяч девятьсот девяносто девять.

Подсказка:

В зависимости от количества знаков называют числа:

2 знака – двузначное.
3 знака – трёхзначное и т.д.

Помни о том, как расположены числа на луче натуральных чисел: чем левее, тем оно меньше, а чем правее – тем больше.
Для того, чтобы прочитать число, читай отдельно количество единиц наивысшего класса и так до наименьшего. При этом называния разрядом класса единиц не называют.

Шаг 1.
Находим и называем числа.

Наименьшее семизначное число – 1000000 – один миллион.
Наибольшее пятизначное число – 99999 – девяносто девять тысяч девятьсот девяносто девять.

Шаг 2.
Оформляем задание в тетрадь.

Номер 33.

Покупателю продали дыни по одинаковой цене за 1 кг: одну массой 5 кг, другую массой 3 кг. Вся эта покупка стоила а р. Запиши по данному условию выражения, которые показывают:

1) сколько стоил 1 кг дыни; 2) сколько стоила каждая дыня.

Ответ:

1) а : (5 + 3); 2) а : (5 + 3) ∙ 5, а : (5 + 3) ∙ 3.

Подсказка:

Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а ∙ 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:

   1 множитель ∙ 2 множитель = значение произведения.
   Значение произведения : 1 множитель = 2 множитель.
   Значение произведения : 2 множитель = 1 множитель.

Данная задача: вида «цена 1 кг, количество килограмм, общая стоимость» характеризуется зависимостями между компонентами:

   Цена 1 кг ∙ количество кг = общая стоимость.
   Общая стоимость : количество кг = цена 1 кг.
   Общая стоимость : цена 1 кг = количество кг.

Шаг 1.
Оформляем условие в виде таблицы.