Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 9

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 29.
Вычисли с устным объяснением.
Ответ:
402 – 130
Вычитаю единицы 2 − 0 = 2. Пишу 2 единицы под единицами. Вычитаю десятки. От 0 нельзя отнять 3. Занимаю 1 сотню. 1 сотня – это 10 десятков. Вычитаю 10 − 3 = 7. Пишу под десятками. Вычитаю сотни. Было 4 сотни, 1 занимали, осталось 3. 3 − 1 = 2. Пишу под сотнями.
Ответ: 272
347 – 108
Вычитаю единицы. Вычесть из семи восемь нельзя. Занимаю 1 десяток. 1 десяток – это 10 единиц. Вычитаю 17 − 8 = 9. Записываю под единицами. Вычитаю десятки. 3 − 0 = 3. Записываю под десятками. Вычитаю сотни 3 − 1 = 2. Записываю под сотнями.
Ответ: 239
902 – 555
Вычитаю единицы. Вычесть из двойки пятёрку нельзя. Занять у нуля нельзя. Занимаю 1 сотню. 1 сотня – это 10 десятков. 1 десяток отдаем. Вычитаю 12 − 5 = 7. Пишу под единицами. Вычитаю десятки. Было 10 десятков, один занимали, осталось 9. 9 − 5 = 4. Пишу под десятками. Вычитаю сотни. Было 9 сотен, одну занимали, осталось 8. 8 − 5 = 3. Пишу под сотнями.
Ответ: 347
807 – 438
Вычитаю единицы. От 7 нельзя отнять 8. Занимаю 1 десяток. Но десятков нет. Занимаю 1 сотню. 1 сотня – это 10 десятков. 1 десяток – это 10 единиц. Вычитаю 17 − 8 = 9. Записываю под единицами. Вычитаю десятки. Было 10 десятков, 1 занимали, осталось 9. 9 − 3 = 6. Записываю под десятками. Вычитаю сотни. Было 8 сотен, одну занимали, осталось 7. 7 − 4 = 3. Записываю под сотнями.
Ответ: 369
604 – 88
Вычитаю единицы. От 4 отнять 8 нельзя. Занимаю 1 десяток. Но десятков нет. Занимаю 1 сотню. 1 сотня – это 10 десятков. 1 десяток – это 10 единиц. Вычитаю 14 − 8 = 6. Пишу под единицами. Вычитаю десятки. Было 10 десятков, 1 занимали, осталось 9. 9 − 8 = 1. Записываю под десятками. Из 6 сотен остаётся 5, так как занимали. Записываю под сотнями.
Ответ: 516
Следуем плану при устном объяснении вычитания в столбик:
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) вычитаю десятки;
6) вычитаю сотни;
7) вычитание окончено. Читаю ответ.
Разберём на примере.
402 – 130
Записываю уменьшаемое 402, ставлю знак –, записываю вычитаемое 130 таким образом, чтобы единицы под единицами и т.д., провожу черту.
Вычитаю единицы 2 – 0 = 2. Пишу 2 единицы под единицами.
Вычитаю десятки. От 0 нельзя отнять 3. Занимаю 1 сотню. 1 сотня – это 10 десятков. Вычитаю 10 – 3 = 7. Пишу под десятками.
Вычитаю сотни. Было 4 сотни, 1 занимали, осталось 3. 3 – 1 = 2. Пишу под сотнями.
Вычитание окончено. Читаем ответ: 272.
Аналогично проговариваем остальные выражения.
Номер 30.
В хор записалось 36 человек, а в кружок по рисованию – на 5 человек меньше. Сколько человек записалось в кружок по рисованию?
Ответ:
36 − 5 = 31 (чел.). Ответ: 31 человек записалось в кружок по рисованию.
«на 5 человек меньше», значит, будем вычитать.
Условие оформляем в виде краткой записи.
Оформляем условие.

На хор записались 36 человек, а в кружок по рисования – на 5 человек меньше.
Рассуждаем.
В кружок по рисованию записались столько же людей, сколько на хор, но без 5 человек. Поэтому, чтобы узнать, сколько людей записалось в кружок по рисованию, нужно из количества людей на хоре вычесть 5 человек.
36 – 5 = 31 (чел.).
Записываем ответ.
Ответ: 31 человек записалось в кружок по рисованию.
Номер 31.
Начерти и вырежи 4 таких треугольника, сложи из них квадрат, начерти его в тетради. Вычисли периметр полученного квадрата в миллиметрах.


Сторона квадрата 28 мм.
P = сторона ∙ 4
P = 28 ∙ 4 = 112 мм
Ответ: периметр квадрата составляет 112 мм
Помним, что периметр любой геометрической фигуры – это сумма длин всех её сторон.
Квадрат – правильный четырёхугольник, у которого все стороны равны между собой, т.е. одинаковые.
Вырежем фигуры.
Начертим и вырезаем 4 одинаковые треугольника, составляем из них квадрат, начертим его в тетради.
Найдём периметр.
Чтобы вычислить длину квадрата, нужно измерить длину всех сторон, а полученные длины сложить.
Но длина стороны квадрата одинаковая. Поэтому сложение одинаковых слагаемых можно заменить умножением. Тогда, P = а · 4.
Сторона квадрата – 28 мм.
P = сторона ∙ 4.
P = 28 ∙ 4 = 112 мм.
Записываем ответ.
Ответ: 112 мм.
Номер 32.
В купейном вагоне 36 мест, а в плацкартном – на 18 мест больше. Сколько мест в плацкартном и купейном вагонах вместе?
Ответ:
1) 36 + 18 = 54 (м.) – в плацкартном вагоне.
2) 36 + 54 = 90 (м.) – мест
Ответ: 90 мест в плацкартном и купейном вагонах всего.
«на 18 мест больше», значит, вычисляется сложением
«всего», значит, вычисляется сложением.
Задача на нахождение целого.
Оформляем условие в виде краткой записи.
Оформляем условие.
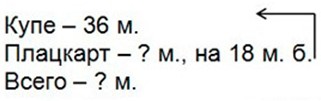
В купейном вагоне 36 мест, а в плацкартном – на 18 мет больше.
Рассуждаем.
На 18 мест больше, значит, в плацкартном вагоне столько же мест, сколько в купейном и еще 18 мест. Поэтому, чтобы узнать, сколько мест в плацкартном вагоне, нужно к количеству мест в купейном прибавить 18 мест.
1) 36 + 18 = 54 (м.) – в плацкартном вагоне.
Продолжаем рассуждения.
Общее количество мест в вагонах складывается из количества мест в купейном вагоне и плацкартном. Чтобы узнать, сколько мест в двух вагонах, нужно сложить количество мест каждого из вагонов.
2) 36 + 54 = 90 (м.).
Записываем ответ.
Ответ: 90 мест всего.
Решение в виде выражения: 36 + (36 + 18) = 90 (м.).
Номер 33.
Найди значение выражений а + 347 и а − 39, если а = 40, а = 53, а = 282, а = 558.
Ответ:При а = 40
При а = 53
При а = 282
При а = 558
а + 347
40 + 347 = 387
53 + 347 = 400
282 + 347 = 629
558 + 347 = 905
а − 39
40 − 39 = 1
53 − 39 = 14
282 − 39 = 243
558 − 39 = 519
а + 347, значит, увеличить число а на 347 единиц, т.е. прибавить 347.
а – 39, значит, уменьшить число а на 39 единиц, т.е. вычесть 39.
Вычисление значений выражения сводится к применению правил:
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с.
Правило вычитания числа из суммы:
(а + в) – с = (а – с) + в.
Подставляем вместо а данное число и находим значение выражения.
a + 347
40 + 347 = 40 + (340 + 7) = (340 + 40) + 7 = 380 + 7 = 387, по правилу прибавления суммы к числу.
53 + 347 = 53 + (340 + 7) = 340 + (53 + 7) = 340 +60 = 400, по правилу прибавления суммы к числу.

a – 39
40 – 39 = 40 – (30 + 9) = (40 – 30) – 9 = 10 – 9 = 1, по правилу вычитания суммы из числа.
347 – 39 = (300 + 47) – 39 = 300 + (47 – 39) = 300 + 8 = 308, по правилу вычитания числа из суммы.
282 – 39 = (200 + 82) – 39 = 200 + (82 – 39) = 200 + 43 = 243. по правилу вычитания числа из суммы.
558 – 39 = (500 + 58) – 39 = 500 – (58 – 39) = 500 – 19 = 481, по правилу вычитания числа из суммы.
Оформляем задание в тетрадь.
а + 347
Если, а = 40, то 40 + 347 = 387
Если, а = 53, то 53 + 347 = 400
Если, а = 282, то 282 + 347 = 629
Если, а = 558, то 558 + 347 = 905
а – 39
Если, а = 40, то 40 – 39 = 1
Если, а = 53, то 53 – 39 = 14
Если, а = 282, то 282 – 39 = 243
Если, а = 558, то 558 – 39 = 519
Номер 34.
Сравни выражения:
Ответ:
Прежде, чем сравнивать выражения, необходимо вычислить их значения, выполнив действия.
Помним порядок выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
находим значения выражений.
200 – 30 · 4 и (200 – 30) · 4
200 – 30 · 4 = 200 – 120 = 80
(200 – 30) · 4 = 170 · 4 = 17 дес. · 4 = 68 дес. = 680
Сравниваем полученные значения.
80 < 680, значит, 200 – 30 · 4 < (200 – 30) · 4
Выполняем аналогичные этапы с остальными неравенствами.
72 : (4 · 2) и 72 : 4 · 2
72 : (4 · 2) = 72 : 8 = 9
72 : 4 · 2 = 18 · 2 = 36
9 < 36, значит, 72 : (4 · 2) < 72 : 4 · 2
480 : 2 · 3 и 480 : (2 · 3)
480 : 2 · 3 = 240 · 3 = 24 дес. · 3 = 72 дес. = 720
480 : (2 · 3) = 480 : 6 = 48 дес. : 6 = 8 дес. = 80
720 > 80, значит, 480 : 2 · 3 > 480 : (2 · 3)
350 : 5 · 2 и 350 : (5 · 2)
350 : 5 · 2 = 70 · 2 = 140
350 : (5 · 2) = 350 : 10 = 35
140 > 35, значит, 350 : 5 · 2 > 350 : (5 · 2).
Номер 35.
Найди сумму.
Ответ:
1) Помним, что вычислить сумму нескольких слагаемых можно разными способами. Мы будем использовать 2 способ.

Вычисляем значение суммы сразу трех слагаемых так: количество единиц значения суммы складывается из суммы количества единиц всех слагаемых. Аналогично с десятками и сотнями.
2) Помним порядок выполнения арифметических действий и что скобки влияют на порядок выполнения действий. Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Находим значение суммы 2 способом.
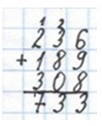
Находим значения выражений.
Расставляем порядок действий согласно правилу.
Выполняем действия и находим значение выражения.
2)
(200 – 30) · 5 =850
1) 200 – 30 = 170
2) 170 · 5 = 850
300 + 90 : 3 = 330
1) 90 : 3 = 30
2) 300 + 30 = 330
50 · 4 + 90 · 3 = 470
1) 50 · 4 = 200
2) 90 · 3 = 270
3) 200 + 270 = 470
70 · 3 + 80 : 10 = 218
1) 70 · 3 = 210
2) 80 : 10 = 8
3) 210 + 8 = 218
27 : (9 · 3) = 1
1) 9 · 3 = 27
2) 27 : 27 = 1
68 : 2 : 2 = 17
1) 68 : 2 = 34
2) 34 : 2 = 17.
Номер 36.
1) Как убрать 1 палочку, чтобы осталось 3 квадрата?
2) По тому же рисунку скажи, как добавить 2 палочки, чтобы получилось 5 одинаковых квадратов.


Для решения задачи лучше выполнять реальные действия со счетными палочками или спичками, чтобы увидеть решение задачи.
Задание внизу страницы.
Вычисли.
Ответ:
Следуем плану при устном объяснении вычитания в столбик:
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) вычитаю десятки;
6) вычитаю сотни;
7) вычитание окончено. Читаю ответ.
Выполняем вычитание.
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом:
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда.
3 ед. – 9 ед, вычесть нельзя, значит, занимаю 1 десяток. 1 дес – это 10 ед. да еще 3 ед. – 13ед. Значит, 13 ед. – 9 ед. = 4 ед.
4 ед. меньше, чем 10 ед., значит, 4 ед. записываю в значение разности.
5) вычитаю десятки. В уменьшаемом 0 десятков, значит, занимаю 1 сот. – это 10дес. Да еще занимали 1 дес – 9 дес. Тогда, 9 дес – 2 дес. = 7 дес.
7 дес. меньше, чем 10 дес., значит, записываю 7 десятков в значение уменьшаемого.
6) вычитаю сотни. В уменьшаемом 5 сот, да еще 1 сот. занимали, то 5 сот. – 1 сот. = 4 сот. Тогда, 4 сот – 2 сот = 2 сот. 2 сот. меньше, чем 10 сот., значит, записываю в значении разности 2 сот.
7) вычитание окончено. Читаю ответ.
Значение разности от вычитания 229 из 503 равно 274.
Аналогично выполняем следующее вычитание.
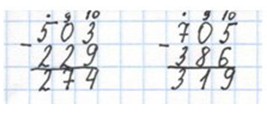
Оформляем задание в тетрадь.
Задание на полях страницы.


1) Помним, что вычислить сумму нескольких слагаемых можно разными способами. Мы будем использовать 2 способ.
Вычисляем значение суммы сразу трех слагаемых так: количество единиц значения суммы складывается из суммы количества единиц всех слагаемых. Аналогично с десятками и сотнями.

Находим значение суммы 2 способом вставляя пропущенные цифры.
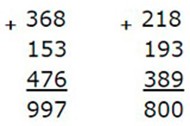
Номер 30.
Вычисли с устным объяснением.
Ответ:
402 – 130
Вычитаю единицы 2 − 0 = 2. Пишу 2 единицы под единицами. Вычитаю десятки. От 0 нельзя отнять 3. Занимаю 1 сотню. 1 сотня – это 10 десятков. Вычитаю 10 − 3 = 7. Пишу под десятками. Вычитаю сотни. Было 4 сотни, 1 занимали, осталось 3. 3 − 1 = 2. Пишу под сотнями.
Ответ: 272
347 – 108
Вычитаю единицы. Вычесть из семи восемь нельзя. Занимаю 1 десяток. 1 десяток – это 10 единиц. Вычитаю 17 − 8 = 9. Записываю под единицами. Вычитаю десятки. 3 − 0 = 3. Записываю под десятками. Вычитаю сотни 3 − 1 = 2. Записываю под сотнями.
Ответ: 239
902 – 555
Вычитаю единицы. Вычесть из двойки пятёрку нельзя. Занять у нуля нельзя. Занимаю 1 сотню. 1 сотня – это 10 десятков. 1 десяток отдаем. Вычитаю 12 − 5 = 7. Пишу под единицами. Вычитаю десятки. Было 10 десятков, один занимали, осталось 9. 9 − 5 = 4. Пишу под десятками. Вычитаю сотни. Было 9 сотен, одну занимали, осталось 8. 8 − 5 = 3. Пишу под сотнями.
Ответ: 347
807 – 438
Вычитаю единицы. От 7 нельзя отнять 8. Занимаю 1 десяток. Но десятков нет. Занимаю 1 сотню. 1 сотня – это 10 десятков. 1 десяток – это 10 единиц. Вычитаю 17 − 8 = 9. Записываю под единицами. Вычитаю десятки. Было 10 десятков, 1 занимали, осталось 9. 9 − 3 = 6. Записываю под десятками. Вычитаю сотни. Было 8 сотен, одну занимали, осталось 7. 7 − 4 = 3. Записываю под сотнями.
Ответ: 369
604 – 88
Вычитаю единицы. От 4 отнять 8 нельзя. Занимаю 1 десяток. Но десятков нет. Занимаю 1 сотню. 1 сотня – это 10 десятков. 1 десяток – это 10 единиц. Вычитаю 14 − 8 = 6. Пишу под единицами. Вычитаю десятки. Было 10 десятков, 1 занимали, осталось 9. 9 − 8 = 1. Записываю под десятками. Из 6 сотен остаётся 5, так как занимали. Записываю под сотнями.
Ответ: 516
Номер 31.
Для спортивного клуба закупили 10 футбольных мячей и 7 упаковок теннисных мячей, по 12 мячей в каждой упаковке. Сколько всего мячей закупили?
Ответ:1) 12 ∙ 7 = 84 (мяча) – закупили теннисных;
2) 10 + 84 = 94 (мяча) – всего закупили.
Ответ: 94 мяча всего закупили для спортивного клуба.
Номер 32.
Начерти и вырежи 4 таких треугольника, сложи из них квадрат, начерти его в тетради. Вычисли периметр полученного квадрата в миллиметрах.


Сторона квадрата 28 мм.
P = сторона ∙ 4
P = 28 ∙ 4 = 112 мм
Ответ: периметр квадрата составляет 112 мм
Номер 33.
В купейном вагоне 36 мест, а в плацкартном – на 18 мест больше. Сколько мест в плацкартном и купейном вагонах вместе?
Ответ:
1) 36 + 18 = 54 (м.) – в плацкартном вагоне.
2) 36 + 54 = 90 (м.) – всего
Ответ: 90 мест всего в плацкартном и купейном вагонах.
Номер 34.
Найди значение выражений а + 347 и а − 39, если а = 40, а = 53, а = 282, а = 558.
Ответ:При а = 40
При а = 53
При а = 282
При а = 558
а + 347
40 + 347 = 387
53 + 347 = 400
282 + 347 = 629
558 + 347 = 905
а − 39
40 − 39 = 1
53 − 39 = 14
282 − 39 = 243
558 − 39 = 519
Номер 35.
Сравни выражения:
Ответ:200 − 30 ∙ 4 < (200 − 30) ∙ 4
200 − 30 ∙ 4 = 200 − 120 = 80
(200 − 30) ∙ 4 = 170 ∙ 4 = (100 + 70) ∙ 4 = 400 + 280 = 680
80 < 680
72 : (4 ∙ 2) < 72 : 4 ∙ 2
72 : (4 ∙ 2) = 72 : 8 = 9
72 : 4 ∙ 2 = 18 ∙ 2 = 36
9 < 36
480 : 2 ∙ 3 > 480 : (2 ∙ 3)
480 : 2 ∙ 3 = 240 ∙ 3 = 720
480 : (2 ∙ 3) = 480 : 6 = 80
720 > 80
350 : 5 ∙ 2 > 350 : (5 ∙ 2)
350 : 5 ∙ = 70 ∙ 2 = 140
350 : (5 ∙ 2) = 350 : 10 = 35
140 > 35
Номер 36.
Найди сумму: 236 + 189 + 308.
Ответ:
Номер 37.
1) Как убрать 1 палочку, чтобы осталось 3 квадрата?
2) По тому же рисунку скажи, как добавить 2 палочки, чтобы получилось 5 одинаковых квадратов.


Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы


С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.