Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 26

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 107.
Замени каждое число суммой разрядных слагаемых:
Ответ:205 = 200 + 5
205000 = 200000 + 5000
205040 = 200000 + 5000 + 40
1648 = 1000 + 600 + 40 + 8
640008 = 600000 + 40000 + 8
164800 = 100000 + 60000 + 4000 + 800
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.

Заполним таблицу.
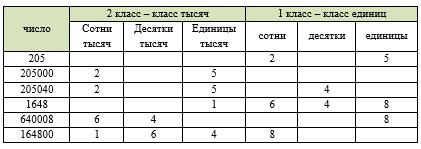
Запишем числа в виде сумм разрядных слагаемых.
205 = 200 + 5
205000 = 200000 + 5000
205040 = 200000 + 5000 + 40
1648 = 1000 + 600 + 40 + 8
640008 = 600000 + 40000 + 8
164800 = 100000 + 60000 + 4000 + 800
Номер 108.
Ответ:90000 + 3000 + 1 = 93001 300206 − 300000 − 6 = 200
Задание имеет 2 пути выполнения:
1) Записать число используя сумму его разрядных слагаемых и записать число используя разность его разрядных.
2) Найти значение выражений.
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.

Номер 109.
Сколько цифр потребуется для записи числа, высший разряд которого − сотни тысяч? десятки тысяч?
Ответ:6 цифр, например, 100000 5 цифр, например, 34567
Помним о том, в каком порядке следуют разряды:
единицы,
десятки,
тысячи,
единицы тысяч,
десятки тысяч,
сотни тысяч.
Каждый разряд обозначается одной цифрой, поэтому количество знаков можно узнать, если посмотреть, сколько в числе разрядов. И наоборот: сколько знаков в числе, столько в нем будет и разрядов.
Номер 110.
Вставь числа, пропущенные при счете 9997, 9998, ..., 10001, 10002.
Ответ:9999, 10000
Вспомним свойства натурального ряда чисел. Несколько из них помогут для формулировки ответа на вопрос. Натуральные числа – числа, которые используют при счете предметов (1, 2, 3 и т.д.).
Вспомним свойства натурального ряда чисел.
1) Ряд натуральных чисел имеет начало, но не имеет конца.
2) Между двумя соседними натуральными числами нет другого натурального числа.
3) Если к любому натуральному числу прибавить 1, то получится число, следующее за данным, т.е. которое мы называем при счете после данного.
4) Если из любого натурального числа вычесть 1, то получится число предыдущее, то, которое мы называем при счете перед данным.
Воспользуемся свойством и заполним пропуски.
9998 + 1 = 9999
9999 + 1 = 10000
Получаем: 9997, 9998, 9999, 10000, 10001, 10002.
Номер 111.
Выпиши названия всех равных отрезков. Найди периметр и площадь прямоугольника ABCD.

AD = BС, AB = CD, AC = BD, BK = CK = DK = AK. Периметр прямоугольника ABCD: 2 ∙ 3 + 2 ∙ 5 = 6 + 10 = 16 (см) Площадь прямоугольника ABCD: 3 ∙ 5 = 15 (см2)
Периметр прямоугольника – сумма длин всех сторон.
Площадь фигуры – часть плоскости, занятая фигурой. Значит, чтобы узнать, чему равна площадь прямоугольника, нужно длину умножить на ширину.
Отрезок – геометрическая фигура, часть прямой, ограниченная с двух сторон точками. Длина отрезка – расстояние между точками.
Равные отрезки, т.е. имеющие равное расстояние между точками.
Найдём равные отрезки.
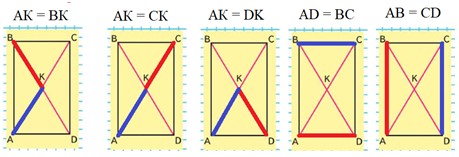
Найдём периметр прямоугольника ABCD.
Периметр прямоугольника – сумма длин всех сторон.
Длина – 5 см.
Ширина – 3 см.
Р = 2 ∙ 3 + 2 ∙ 5 = 6 + 10 = 16 (см).
Найдём площадь прямоугольника ABCD.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину.
S = 5 · 3 = 15 см2.
Номер 112.
Составь и реши задачу.

На фабрике ежедневно расходуется 10 кг сахара. За сколько дней израсходовали 80 кг сахара?
80 : 10 = 8 (дн.)
Ответ: за 8 дней всего израсходовали 80 кг сахара.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Расход сахара в 1 день · количество дней = общий расход сахара.
Общий расход сахара : количество дней = расход сахара в 1 день.
Общий расход сахара : расход сахара в 1 день = количество дней.
Рассуждаем.

На фабрике ежедневно расходуется 10 кг сахара. За сколько дней израсходовали 80 кг сахара?
Рассуждаем.
Общий расход сахара складывается из расхода сахара в каждый из дней. Значит, чтобы узнать, на сколько дней хватит сахара, нужно общий расход сахара разделить на расход сахара в 1 день.
80 : 10 = 8 (дн.).
Записываем ответ.
Ответ: за 8 дней.
Номер 113.
В январе было 14 солнечных дней, в феврале − на 6 дней меньше, чем в январе, а в марте − в 2 раза больше, чем в феврале. Поставь вопрос и реши задачу.
Ответ:Сколько солнечных дней всего было в течение трёх месяцев?

1) 14 − 6 = 8 (дн.) – было в феврале.
2) 8 ∙ 2 = 16 (дн.) – было в марте.
3) 14 + 8 + 16 = 38 (дн.) – всего.
Ответ: 38 солнечных дней всего было за три месяца.
«На 6 дней меньше», значит, вычисляется вычитанием.
«В 2 раза больше», значит, вычисляется умножением.
«всего», значит, вычисляется сложением.
Оформляем условие в виде краткой записи и поставим вопрос.
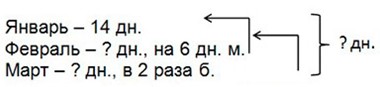
Рассуждаем.
Чтобы узнать, сколько дней было в феврале, нужно из количества солнечных дней января вычесть 6 дней.
1) 14 − 6 = 8 (дн.) – было в феврале.
Продолжаем рассуждение.
Чтобы узнать, сколько солнечных дней было в марте, нужно количество солнечных дней февраля умножить на 2.
2) 8 ∙ 2 = 16 (дн.) – было в марте.
Продолжаем рассуждение.
Общее количество солнечных дней складывается из количеств солнечных дней в каждом месяце. Значит, чтобы узнать, сколько солнечных дней было всего, нужно сложит количество солнечных дней каждого месяца.
3) 14 + 8 + 16 = 38 (дн.) – всего.
Записываем ответ.
Ответ: 38 солнечных дней за три месяца.
Решение выражением: 14 + (14 – 6) + (14 – 6) · 2 = 38.
Номер 114.
Построй диаграмму количества солнечных дней по месяцам, используя решение задачи 113. (Обозначай 2 дня одной клеткой.)
Ответ:
Диаграмма – источник информации о каком-либо явлении, предметах.
По горизонтали расположены названия месяцев, а по вертикали – количество солнечных дней каждого месяца.
Единица измерения, т.е. масштаб: 2 дня – 1 клетка.
Проанализируем данные.
Январь – 14 солнечных дней.
Февраль – 8 солнечных дней.
Март – 16 солнечных дней.
Масштаб: 2 солнечных дня – 1 клетка.
Рассуждаем.
Чтобы узнать, сколько клеток будет составлять количество солнечных дней месяца, нужно общее количество разделить на масштаб.
14 : 2 = 7 клеток – январь.
8 : 2 = 4 клетки – февраль.
16 : 2 = 8 клеток – март.
Построим диаграмму.
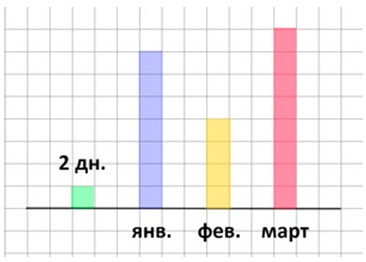
Номер 115.
Проверь, верны ли неравенства.
Ответ:99 ∙ 9 < 691 – неверно.
99 ∙ 9 = 891
891 > 691
207 ∙ 4 > 820 – верно.
207 ∙ 4 = 828
828 > 820
209 > 872 : 8 – верно.
872 : 8 = 109
209 > 109
125 < 945 : 7 – верно.
945 : 7 = 135
125 < 135
68 < 774 : 9 – верно.
774 : 9 = 86
68 < 86
160 > 996 : 6 – неверно.
996 : 6 = 166
160 < 166
Для того, чтобы понять, верно ли равенство – вычисли значение выражения, а полученные значения сравни.
Найдём значение выражений и сравним левую и правую части.
99 ∙ 9 < 691 – неверно.
99 ∙ 9 = 891
891 > 691
207 ∙ 4 > 820 – верно.
207 ∙ 4 = 828
828 > 820
209 > 872 : 8 – верно.
872 : 8 = 109
209 > 109
125 < 945 : 7 – верно.
945 : 7 = 135
125 < 135
68 < 774 : 9 – верно.
774 : 9 = 86
68 < 86
160 > 996 : 6 – неверно.
996 : 6 = 166
160 < 166
Оформляем задание.

Номер 116.
Узнай какие числа прячутся под треугольником, квадратом и кругом. Помни, что во всех равенствах одна и та же фигура обозначает одно и тоже число.

70 + 50 = 120
50 + 180 = 230
70 + 230 = 300
Ответ: треугольник – 70, квадрат – 50, круг – 180.
Начинаем решение с того равенства, где больше известных чисел. Начинаем с равенства 3.
Найдём значение треугольника.
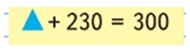
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
300 – 230 = 70
Треугольник = 70
Найдём значение квадрата.

Подставляем значение треугольника в первое равенство:
70 + К = 120
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
120 – 70 = 50
Квадрат = 50
Найдём значение круга.

Подставляем значение квадрата во второе равенство:
50 + Кр = 230
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
230 – 50 = 180
Круг = 180
Найдём значение круга.
Ответ: треугольник – 70, квадрат – 50, круг – 180.
Задание внизу страницы.
Ответ:600000 + 1000 + 30 = 601030 905340 − 900000 − 300 = 5040
Задание имеет 2 пути выполнения:
1) Записать число используя сумму его разрядных слагаемых и записать число используя разность его разрядных.
2) Найти значение выражений.
При необходимости обращайтесь к таблице, чтобы вспомнить классово-разрядный состав числа.

Номер 111.
Замени каждое число суммой разрядных слагаемых:
Ответ:205 = 200 + 5
205000 = 200000 + 5000
205040 = 200000 + 5000 + 40
1648 = 1000 + 600 + 40 + 8
640008 = 600000 + 40000 + 8
164800 = 100000 + 60000 + 4000 + 800
Номер 112.
Ответ:90000 + 3000 + 1 = 93001 300206 − 300000 − 6 = 200
Номер 113.
Сколько цифр потребуется для записи числа, высший разряд которого − сотни тысяч? десятки тысяч?
Ответ:6 цифр, например, 100000 5 цифр, например, 34567
Номер 114.
Вставь числа, пропущенные при счете 9997, 9998, ..., 10001, 10002.
Ответ:9999, 10000
Номер 115.
Выпиши названия всех равных отрезков. Найди периметр и площадь прямоугольника ABCD.

AD = BС, AB = CD, AC = BD, BK = CK = DK = AK. Периметр прямоугольника ABCD: 2 ∙ 3 + 2 ∙ 5 = 6 + 10 = 16 (см) Площадь прямоугольника ABCD: 3 ∙ 5 = 15 (см2)
Номер 116.
Составь и реши задачу.

На фабрике ежедневно расходуется 10 кг сахара. За сколько дней израсходовали 80 кг сахара?
80 : 10 = 8 (дн.)
Ответ: за 8 дней всего израсходуют 80 кг сахара.
Номер 117.
В январе было 14 солнечных дней, в феврале − на 6 дней меньше, чем в январе, а в марте − в 2 раза больше, чем в феврале. Поставь вопрос и реши задачу.
Ответ:Сколько солнечных дней всего было в течение трёх месяцев?

1) 14 − 6 = 8 (дн.) – было в феврале.
2) 8 ∙ 2 = 16 (дн.) – было в марте.
3) 14 + 8 + 16 = 38 (дн.) – всего.
Ответ: 38 солнечных дней всего было за три месяца.
Номер 118.
Построй диаграмму количества солнечных дней по месяцам, используя решение задачи 117. (Обозначай 2 дня одной клеткой.)
Ответ:
Номер 119.
Проверь, верны ли неравенства.
Ответ:99 ∙ 9 < 691 – неверно.
99 ∙ 9 = 891
891 > 691
207 ∙ 4 > 820 – верно.
207 ∙ 4 = 828
828 > 820
209 > 872 : 8 – верно.
872 : 8 = 109
209 > 109
125 < 945 : 7 – верно.
945 : 7 = 135
125 < 135
68 < 774 : 9 – верно.
774 : 9 = 86
68 < 86
160 > 996 : 6 – неверно.
996 : 6 = 166
160 < 166
Номер 120.
Узнай какие числа прячутся под треугольником, квадратом и кругом. Помни, что во всех равенствах одна и та же фигура обозначает одно и тоже число.

70 + 50 = 120
50 + 180 = 230
70 + 230 = 300
Ответ: треугольник – 70, квадрат – 50, круг – 180.
Задание внизу страницы.
Ответ:600000 + 1000 + 30 = 601030 905340 − 900000 − 300 = 5040
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.