Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 25

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 100.
Запиши и прочитай числа, в которых:
1) 30 единиц II класса и 870 единиц I класса; 2) 8 единиц II класса и 600 единиц I класса; 3) 104 единицы II класса, а единицы I класса отсутствует.
Ответ:1) 30870 – тридцать тысяч восемьсот семьдесят; 2) 8600 – восемь тысяч шестьсот; 3) 104000 – сто четыре тысячи.
Следуйте плану, чтобы записать число цифрами:
1) записывают, сколько всего единиц высшего (второго) класса в числе;
2) записывают, сколько всего единиц следующего (первого) класса в числе.
Записываем числа по плану.
30 единиц II класса и 870 единиц I класса;
1) записывают, сколько всего единиц высшего класса в числе: 30.
2) записывают, сколько всего единиц следующего класса в числе: 870.
Получаем число: 30 870.
8 единиц II класса и 600 единиц I класса;
1) записывают, сколько всего единиц высшего класса в числе: 8.
2) записывают, сколько всего единиц следующего класса в числе: 600.
Получаем число: 8 600.
104 единицы II класса, а единицы I класса отсутствует..
1) записывают, сколько всего единиц высшего класса в числе: 104.
2) записывают, сколько всего единиц следующего класса в числе: 000.
Получаем число: 104 000.
Оформляем задание в тетрадь.
30870 – тридцать тысяч восемьсот семьдесят.
8600 – восемь тысяч шестьсот.
104000 – сто четыре тысячи.
Номер 101.
1) Запиши числа цифрами. Наименьшее расстояние от Земли до Луны составляет триста пятьдесят шесть тысяч четыреста девять километров, а наибольшее − четыреста шесть тысяч семьсот сорок километров. 2) Что обозначает каждая цифра в записи этих чисел?
Ответ:1) 356409 км – 3 сотни тысяч, 5 десятков тысяч, 6 единиц тысяч, 4 сотни, 0 десятков, 9 единиц 2) 406740 км – 4 сотни тысяч, 0 десятков тысяч, 6 единиц тысяч, 7 сотен, 4 десятка, 0 единиц.
Следуйте плану, для того, чтобы записать многозначное число:
1) записываю сколько единиц в числе высшего разряда.
2) записываю количество единиц следующего разряда.
3) Прочитываю число по плану на с.24 для самопроверки:
1. разбей число на классы, отсчитывая справа по 3 цифры.
2. читай, сколько в числе единиц каждого класса, начиная с высшего, не произнося название классе единиц.
Записываем числа по плану и читаю.
Триста пятьдесят шесть тысяч четыреста девять километров – 356 единиц высшего разряда, 409 единиц низшего разряда.
Четыреста шесть тысяч семьсот сорок – 406 единиц высшего разряда, 740 единиц низшего разряда.
Оформляем задание в тетрадь.
356409 км – 3 сотни тысяч, 5 десятков тысяч, 6 единиц тысяч, 4 сотни, 0 десятков, 9 единиц.
406740 км – 4 сотни тысяч, 0 десятков тысяч, 6 единиц тысяч, 7 сотен, 4 десятка, 0 единиц.
Номер 102.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполняем письменное деление.
804 : 4
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 8 сотен, значит, в частном будет 3 цифры.
2) Нахожу цифру сотен в частном: 8 сот : 4 = 2 сот.
3) Нахожу, сколько сотен разделили: 2 сот · 4 = 8 сот.
4) Нахожу, сколько сотен осталось разделить: 8 сот. – 8 сот. = 0 сот. 0 сот. < 4 ., значит, в частном 2 сотни.
5) Образую второе неполное делимое: 0 сот – это 0 дес. да еще 0 дес. – это 0 десятков, значит, в частном 0 десятков.
6) Образую третье неполное делимое: 4 ед.
7) Нахожу количество единиц в частном: 4 ед.: 4 = 1 ед.
8) Нахожу, сколько единиц разделили: 1 ед. · 4 = 4 ед.
9) Нахожу, сколько единиц осталось разделить: 4 ед. – 4 ед. = 0. 0 ед. < 4., значит, деление окончено.
10) Читаю ответ: значение частного от деления 804 на 4 равно 201.
Аналогично выполняем: (627 : 3)
Оформляем задание в тетрадь.
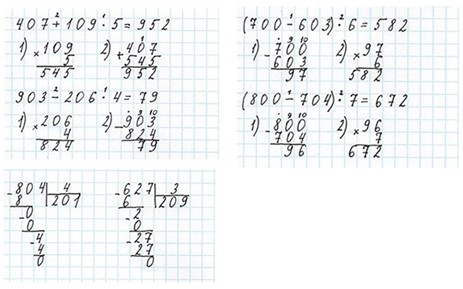
Номер 103.
Купили 3 пакета семян тыквы, по 200 г в каждом, и 3 пакета семян укропа, по 100 г в каждом. на сколько граммов больше купили семян тыквы, чем семян укропа?
Ответ:
1) 200 · 3 = 600 (г) – семян тыквы.
2) 100 · 3 = 300 (г) – семян укропа.
3) 600 − 300 = 300 (г)
Выражением:
200 · 3 – 100 · 3 = 300 (г)
Ответ: на 300 граммов больше купили семян тыквы, чем семян укропа.
1) 200 – 100 = 100 (г) – на сколько грамм больше в 1 пакете
2) 100 · 3 = 300 (г) – на сколько всего больше
Ответ: на 300 г.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Масса 1 пакетика · количество пакетиков = общее количество семян.
Общее количество семян : количество пакетиков = масса 1 пакетика.
Общее количество семян : масса 1 пакетика = количество пакетиков.
Оформляем условие в виде краткой записи или таблицы.

или

Рассуждаем.
Общая масса семян в пакетиках складывается из количества семян каждого пакетика, при этом количество семян каждого пакетика одинаковое. Значит, чтобы узнать, сколько было всего семян, нужно массу 1 пакетика умножить на количество пакетиков. Таким образом находим семена тыквы и укропа.
1) 200 ∙ 3 = 600 (г) – семян тыквы.
2) 100 ∙ 3 = 300 (г) – семян укропа.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Значит, чтобы узнать, на сколько больше было семян тыквы, чем укропа, нужно из количества семян тыквы вычесть количество семян укропа.
3) 600 – 300 = 300 (г).
Записываем ответ.
Ответ: на 300 граммов больше купили семян тыквы.
Решение выражением: 200 · 3 – 100 · 3 = 300 (г).
Номер 104.
До обеденного перерыва в магазине продали 3 мешка сахарного песка, по 45 кг в каждом, а после перерыва – 5 таких мешков. Объясни, что означают выражения:
Ответ:45 ∙ 5 − 45 ∙ 3 – на сколько больше кг сахара продали после перерыва, чем до перерыва на обед. 45 ∙ 5 + 45 ∙ 3 – количество всего проданного сахара (кг).
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Масса 1 пакета · количество пакетов = общее количество сахара.
Общее количество сахара : масса 1 пакета = количество пакетов.
Общее количество сахара : количество сахара = масса 1 пакетика.
Оформляем условие в виде таблицы.

Рассуждаем.
Общее количество сахара складывается из количества сахара каждого мешка, при этом количество сахара в каждом мешке одинаковое. Значит, чтобы узнать, сколько сахара было продано до обеда всего, нужно массу 1 пакета умножить на количество мешков.
(45 · 3) кг и (45 · 5) кг – до обеда и после обеда.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Значит, чтобы узнать, на сколько больше было продано сахара после обеда, чем до обеда, нужно из количества сахара после обеда вычесть количество сахара до обеда.
45 · 5 – 45 · 3 – на сколько больше кг сахара продали после перерыва, чем до перерыва на обед.
Продолжаем рассуждение.
Общее количество проданного сахара складывается из количества проданного сахара до обеда и после. Значит, чтобы узнать, сколько сахара было продано всего, складываю количество проданного сахара до и после обеда.
45 · 3 + 45 · 5 – количество всего проданного сахара.
Номер 105.
Ответ:
Помним , что в математике есть особые правила относительно умножения, деления, вычитания и сложения.
Правило умножения числа на единицу (а · 1) и единицы на число (1 · а) деления числа на единицу ( а : 1) прибавления к числу единицы (а + 1) правило вычитания единицы из числа (а – 1) и другие.
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
8 + 0 + 0 + 6 = 14 + 0 = 14, если к любому числу прибавить 0, то получится это же число.
8 – 0 + 0 · 6 = 8
1) 0 * 6 = 0, если 0 умножить на любое число, то получится 0.
2) 8 – 0 = 8, если из любого числа вычесть 0, то получится это же число.
3) 8 + 0 = 8, если к любому числу прибавить 0, то получится это же число.
0 : 7 + 0 · 5 + 3 = 3
1) 0 : 7 = 0, если 0 разделить на любое число, то получится 0.
2) 0 · 5 = 0, если 0 умножить на любое число, то получится 0.
3) 0 + 0 = 0, если к 0 прибавить любое число, то получится это же число.
4) 0 + 3 = 3, если к 0 прибавить любое число, то получится это же число.
9 – 0 – 6 · 1 = 3
1) 6 · 1 = 6, если любое число умножить на 1, то получится это же число.
2) 9 – 0 = 9, если из любого числа вычесть 0, то получится это же число.
3) 9 – 6 = 3
9 + 0 + 6 : 1 = 15
1) 6 : 1 = 6, если любое число разделить на 1, то получится это же число.
2) 9 + 0 = 9, если к любому числу прибавить 0, то получится это же число.
3) 9 + 6 = 15
7 : 7 – 0 · (4 + 2) = 1
1) 4 + 2 = 6
2) 7 : 7 = 1, если любое число разделить на само себя, то получится 1.
3) 0 · 1 = 0, если 0 умножить на любое число, то получится 0.
4) 1 – 0 = 1, если из любого числа вычесть 0, то получится это же число.
Оформляем задание в тетрадь.

Номер 106.
«Вот вам 3 таблетки, − сказал доктор. − Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка?
Ответ:
2 + 2 = 4 (ч)
Ответ: через 4 часа будет принята последняя таблетка.
Для того, чтобы найти ответ на задачу, воспользуйся циферблатом, чтобы увидеть решение задачи.
Рассуждаем.
Врач прописал больному 3 таблетки. Он должен пить их через каждые 2 часа. Значит, пациент получил три таблетки сейчас и сейчас же выпил первую.
С этого момента начался отсчет таймера. Ведь через 2 часа он должен выпить вторую таблетку, а еще через 2 часа последнюю третью таблетку.
Запишем числа в таблицу.
Помни, что длинная стрелка – минутная, а короткая часовая.

Из схемы видно, что между временем приёма первой таблетки и последней третьей прошло 4 часа.
Записываем ответ.
Ответ: через 4 часа будет принята последняя таблетка.
Задание внизу страницы
Запиши цифрами число восемьсот две тысячи тридцать восемь.
Ответ:802038
Следуйте плану:
1) Прочитаем число по плану на с.24 для самопроверки:
1. разбей число на классы, отсчитывая справа по 3 цифры.
2. читай, сколько в числе единиц каждого класса, начиная с высшего, не произнося название классе единиц.
2) Записываем число цифрами.
Прочитаем число.
Восемьсот две тысячи тридцать восемь – это 802 единицы второго класса и 38 единиц первого класса.
Проверяем:
1) 802.038
2) 802 единиц второго класса и 38 единиц первого класса.
Записываем число.
802 038
Задание на полях страницы.
Цепочка.

48 : 3 = 16 16 : 4 = 4 4 ∙ 19 = 76 76 − 6 = 70 70 + 30 = 100
Выполним действия по порядку. Первый зеленый треугольник – число, с которого начинать действие.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Вычисление значений выражения сводится к применению правил:
Правило вычитания суммы из числа:
а – (в + с) = (а – в) – с.
Выполняем цепочку вычислений, где ответ предыдущего действия является первым из компонентов следующего действия.
48 : 3 = 16, потому что 3 · 16 = 48, это по 3 – 16 раз, где 3 – одинаковое слагаемое, а 16 – количество одинаковых слагаемых.
16 : 4 = 4, потому что 4 · 4 = 16, это по 4 – 4 раза, где 4 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
4 · 19 = 76, это по 4 – 19 раз, где 4 – одинаковое слагаемое, а 19 – количество одинаковых слагаемых.
76 – 16 = 76 – (10 + 6) = (76 – 6) – 10 = 70 – 10 = 60, по правилу вычитания суммы из числа.
60 + 30 = 6 дес. + 3 дес. = 9 дес. = 90.
Оформляем задание в тетрадь.
48 : 3 = 16
16 : 4 = 4
4 ∙ 19 = 76
76 − 6 = 70
70 + 30 = 100
Номер 104.
Запиши и прочитай числа, в которых:
1) 30 единиц II класса и 870 единиц I класса; 2) 8 единиц II класса и 600 единиц I класса; 3) 104 единицы II класса, а единицы I класса отсутствует.
Ответ:1) 30870 – тридцать тысяч восемьсот семьдесят; 2) 8600 – восемь тысяч шестьсот; 3) 104000 – сто четыре тысячи.
Номер 105.
1) Запиши числа цифрами. Наименьшее расстояние от Земли до Луны составляет триста пятьдесят шесть тысяч четыреста девять километров, а наибольшее − четыреста шесть тысяч семьсот сорок километров. 2) Что обозначает каждая цифра в записи этих чисел?
Ответ:1) 356409 км – 3 сотни тысяч, 5 десятков тысяч, 6 единиц тысяч, 4 сотни, 0 десятков, 9 единиц 2) 406740 км – 4 сотни тысяч, 0 десятков тысяч, 6 единиц тысяч, 7 сотен, 4 десятка, 0 единиц.
Номер 106.
Ответ:
Номер 107.
На комбинат по изготовлению детского питания до обеденного перерыва привезли 3 контейнера с яблоками, по 45 кг в каждом, а после перерыва – 5 таких же контейнеров. Объясни, что означают выражения: 45 ∙ (5 – 3) и 45 ∙ (5 + 3).
Ответ:До перерыва – 3 к. по 45 кг
После перерыва – 5 к. по 45 кг
45 ∙ (5 – 3) = 45 ∙ 2 = 90 (кг) – на сколько больше привезли яблок после перерыва, чем до перерыва;
45 ∙ (5 + 3) = 45 ∙ 8 = 360 (кг) – сколько всего привезли яблок.
Номер 108.
До обеденного перерыва в магазине продали 3 мешка сахарного песка, по 45 кг в каждом, а после перерыва – 5 таких мешков. Объясни, что означают выражения:
Ответ:45 ∙ 5 − 45 ∙ 3 – на сколько больше кг сахара продали после перерыва, чем до перерыва на обед. 45 ∙ 5 + 45 ∙ 3 – количество всего проданного сахара (кг).
Номер 109.
Ответ:
Номер 110.
«Вот вам 3 таблетки, − сказал доктор. − Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка?
Ответ:
2 + 2 = 4 (ч) Ответ: через 4 часа будет принята последняя таблетка.
Задание внизу страницы.
Запиши цифрами число восемьсот две тысячи тридцать восемь.
Ответ:802038
Задание на полях страницы.
Цепочка.

48 : 3 = 16 16 : 4 = 4 4 ∙ 19 = 76 76 − 6 = 70 70 + 30 = 100
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.