Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 18

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Что узнали. Чему научились.
Номер 1.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Выполняем вычисления в первом столбике по действиям.
32 + (96 – 64) : 8 · 2 = 32 + 32 : 8 · 2 = 32 + 8 = 40;
1) 96 – 64 = 32;
2) 32 : 8 = 4;
3) 4 · 2 = 8;
4) 32 + 8 = 40.
32 + (96 – 64) : (8 · 2) = 32 + 32 : 16 = 32 + 2 = 34;
1) 96 – 64 = 32;
2) 8 · 2 = 16;
3) 32 : 16 = 2;
4) 32 + 2 = 34.
(32 + 96 – 64 : 8) · 2 = (128 – 8) · 2 = 120 · 2 = 240.
1) 64 : 8 = 8;
2) 32 + 96 = 128;
3) 128 – 8 = 120;
4) 120 · 2 = 240.
Выполняем вычисления во втором столбике по действиям.
(400 – 160 : 8) : 2 = (400 – 20) : 2 = 380 : 2 = 190;
1) 160 : 8 = 20;
2) 400 – 20 = 380;
3) 380 : 2 = 190.
(400 – 160) : 8 : 2 = 240 : 8 : 2 = 30 : 2 = 15;
1) 400 – 160 = 240;
2) 240 : 8 = 30;
3) 30 : 2 = 15.
(400 – 160) : (8 : 2) = 240 : 4 = 60.
1) 400 – 160 = 240;
2) 8 : 2 = 4;
3) 240 : 4 = 60.
Оформляем задание в тетрадь.
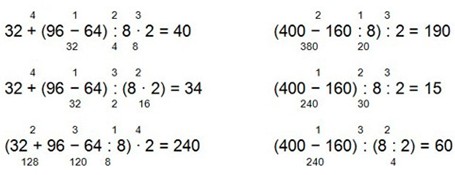
Номер 2.
Ответ:

Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Помним, что существует алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Расставляем порядок действий и выполняем вычисления.
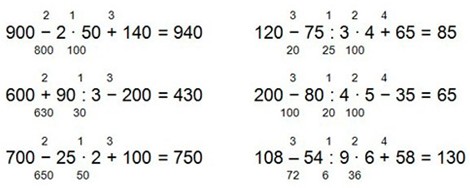
Выполняем письменное деление по алгоритму.
342 : 3
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 3 сот. Высший разряд – сотни, значит, в частном 3 знака.
2) Нахожу цифру сотен в частном: 3 сот. : 3 = 1 сот.
3) Нахожу, сколько сотен разделили: 1 сот. · 3 = 3 сот.
4) Нахожу, сколько сотен осталось разделить: 3 сот. – 3 сот. = 0 сот., 0 сот. < 3, значит, в частном 1 сот.
5) Образую второе неполное делимое: 0 сот. это 0 дес. да еще 4 дес. – 4 дес.
6) Нахожу, количество десятков в частном: 4 дес. : 3 = 1 дес.
7) Нахожу, сколько десятков разделили: 1 дес. · 3 = 3 дес.
8) Нахожу, сколько десятков осталось разделить:
4 дес. – 3 дес. – 1 дес. 1 дес. < 3, значит, в частном 1 десяток.
9) Образую третье неполное делимое: 1 дес. – это 10 ед. да еще 2 ед. – 12 ед.
10) Нахожу количество единиц в частном: 12 ед. : 3 – 4 ед.
11) Нахожу, сколько единиц разделили: 4 ед. · 3 = 12 ед.
12) Нахожу, сколько единиц осталось разделить:
12 ед. – 12 ед. – 0 ед. 0 ед. < 3, значит, в частном 4 единицы.
13) Читаю ответ. Значение частного от деления 342 на 3 равно 114.
Аналогично: (564 : 2, 721 : 7)
Оформляем задание в тетрадь.
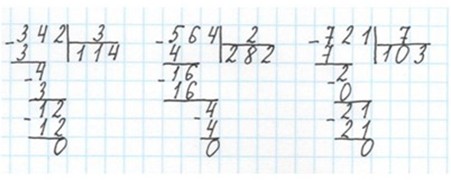
Номер 3.
Сравни числа.
Ответ:796 < 800 312 < 320 1000 > 999
Помним о том, как сравнивают трехзначные числа:
1) Сравниваем сколько знаков в числах. В большем числе количество знаков больше.
2) Если количество знаков одинаковое, сравнивай количество единиц каждого разряда, начиная с высшего. Сравниваю количество сотен.
3) Если количество сотен одинаковое, сравниваю количество десятков.
4) Если количество десятков одинаковое, сравниваю единицы.
5) Делаю вывод о том, какое число больше.
Сравниваем числа по плану.
796 и 800
1) Оба числа трехзначные, т.е. в записи чисел используется 3 знака.
2) Cравниваю количество сотен. В первом числе 7 сотен, а во втором – 8 сотен. 7 сот.<8сот., значит, второе число больше первого.
Тогда, ставлю знак: 796 < 800.
312 и 320
1) Оба числа трехзначные, т.е. в записи чисел используется 3 знака.
2) Cравниваю количество сотен. В первом числе 3 сотни, а во втором – 3 сотни. Количество сотен одинаковое.
3) T.к. количество сотен одинаковое, сравниваю количество десятков. В первом числе 1 десяток, а во втором – 2 десятка. 1 деc. < 2дес., значит, второе число больше первого.
Тогда, ставлю знак: 312 < 320.
1000 и 999
1) Определяю количество знаков. Первое число – четырехзначное, а второе – трехзначное. Значит, первое число больше второго, потому что всегда больше то число, в котором знаков больше.
Тогда, ставлю знак: 1000 > 999.
Оформляем в тетрадь.
796 < 800
312 < 320
1000 > 999
Номер 4.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
36 + 60 : 4 · 2 + 34 = 100
1) 60 : 4 = 15
2) 15 · 2 = 30
3) 36 + 30 = 66
4) 66 + 34 = 100
42 + 54 : 3 · 2 – 18 = 60
1) 54 : 3 = 18
2) 18 · 2 = 36
3) 42 + 36 = 78
4) 78 – 18 = 60
(760 + 100) – (430 + 230) = 200
1) 760 + 100 = 860
2) 430 + 230 = 660
3) 860 – 660 = 200
(970 – 340) + (250 + 120) = 1000
1) 970 – 340 = 630
2) 250 + 120 = 370
3) 630 + 370 = 1000
Оформляем задание в тетрадь.

Номер 5.
Вычисли и проверь деление умножением.
Ответ:
Помним, что существует алгоритм письменного деления:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Вспомни зависимость между компонентами и результатом действия умножения, деления:
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного · делитель = делимое.
Выполняем письменное деление по алгоритму.
624 : 6
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 6 сот.
2) Нахожу цифру сотен в частном: 6 сот. : 6 = 1 сот.
3) Нахожу, сколько сотен разделили: 1 сот. · 6 = 6 сот.
4) Нахожу, сколько сотен осталось разделить: 6 сот. – 6 сот. = 0 сот., 0 сот. < 6, значит, в частном 1 сот.
5) Образую второе неполное делимое: 0 сот. это 0 дес. да еще 2 дес. - 2 дес., 2 дес. < 6, значит спускаю единицы. В частном пишу 0 дес.
6) 2 дес. – это 20 ед. да еще 4 ед. – 24 ед.
7) Нахожу количество единиц в частном: 24 ед. : 6 – 4 ед.
8) Нахожу, сколько единиц разделили: 4 ед. · 6 = 24 ед.
9) Нахожу, сколько единиц осталось разделить:
24 ед. – 24 ед. – 0 ед. 0 ед. < 6, значит, в частном 4 единицы.
10) Читаю ответ. Значение частного от деления 624 на 6 равно 104.
Аналогично выполняем:
963 : 3, 482 : 2, 147 : 7, 135 : 3, 825 : 5, 248 : 8, 616 : 2, 728 : 7, 453 : 3
Выполняем проверку.
Чтобы выполнить проверку необходимо частное умножить на делитель. В ответ должен совпасть с делимым.
Пр: 104 · 6 = 624, 624 = 624 – верно.
Аналогично проводим проверку всех результатов деления.
Оформляем задание в тетрадь.

Номер 6.
Ответ:
Следуем плану при устном объяснении вычитания в столбик:
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) вычитаю десятки;
6) вычитаю сотни;
7) вычитание окончено. Читаю ответ.
Выполняем письменное сложение по алгоритму.
346 + 458 (аналогично 503 + 204, 157 + 484, 308 + 106)
1) Записываю первое слагаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак плюс.
2) Записываю второе слагаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно;
4) Сложение начинаю с единиц низшего разряда; 6 ед. + 8 ед. = 14 ед. 14 ед. – это 1 дес. 4 ед. Значит, 4 единицы записываю под единицами, а 1 десяток запоминаю.
5) Складываю десятки: 4 дес. + 5 дес. = 9 дес. да еще 1 дес. = 10 дес. – это 1 сот. 0 дес. Значит, 0 десятков записываю под десятками, а 1 сотню запоминаю.
6) Складываю сотни: 3 сот. + 4 сот. = 7 сот., да еще 1 сот – 8 сот. 8 сот. < 10 сот., значит, 8 сотен записываю под сотнями.
7) Сложение окончено. Читаю ответ. Значение суммы от сложения 346 и 458 равно 804.
Выполняем письменное вычитание по алгоритму.
832 – 456 (аналогично 621 – 241, 603 – 28, 204 – 39)
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда. Вычитаю единицы; 2 ед. – 6 ед. вычесть нельзя, значит, занимаю 1 дес. Тогда, 12 ед. – 6 ед. = 6 ед. 6 ед. < 10 ед., значит, 6 единиц записываю в разряд единицы.
5) вычитаю десятки; в уменьшаемом 3 десятка да еще 1 дес. занимали – 2 десятка. 2 дес. – 5 дес. вычесть нельзя. Значит, занимаю 1 сот. Тогда, 12 дес. – 5 дес. = 7 дес. 7 дес. < 10 дес., значит, записываю 7 десятков в разряд десятков.
6) вычитаю сотни; в уменьшаемом 8 сотен да еще 1 сот. занимали – 7 сот. Тогда, 7 сот. – 4 сот. = 3 сот. 3 сот. < 10 сот., значит, записываю 3 сотни в разряд сотен.
7) вычитание окончено. Читаю ответ. Значение разности от вычитания 456 из 832 равно 376.
Оформляем задание в тетрадь.
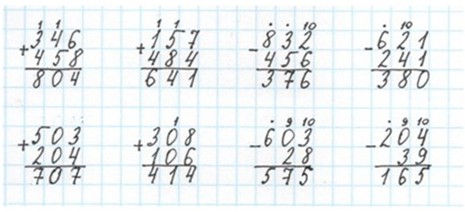
Номер 7.
Ответ:
Помним, что существует алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
5) умножаю десятки;
6) умножаю сотни;
7) Умножение окончено. Читаю ответ.
Помни, что существует алгоритм письменного деления. Следуй ему, объясняя, как выполняешь деление:
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном.
2) Нахожу цифру сотен в частном:
3) Нахожу, сколько сотен разделили:
4) Нахожу, сколько сотен осталось разделить:
5) Образую второе неполное делимое:
6) Нахожу, количество десятков в частном:
7) Нахожу, сколько десятков разделили:
8) Нахожу, сколько десятков осталось разделить:
9) Образую третье неполное делимое:
10) Нахожу количество единиц в частном:
11) Нахожу, сколько единиц разделили:
12) Нахожу, сколько единиц осталось разделить:
13) Читаю ответ.
Выполняем письменное умножение по алгоритму.
318 · 3 (аналогично 247 · 4, 207 · 4, 108 · 6)
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда; 8 ед. · 3 = 24 ед. – это 2 дес. 4 ед. Значит, 4 единицы записываю в разряд единиц, а 2 десятка запоминаю.
5) умножаю десятки; 1 дес. · 3 = 3 дес. да еще 2 дес. – 5 десятков. 5 дес. < 10 дес., значит, в значении произведения 5 десятков.
6) умножаю сотни; 3 сот. · 3 = 9 сот. 9 сот. < 10 сот., значит, в значении произведения 9 сот.
7) Умножение окончено. Читаю ответ. Значение произведения от умножения 318 на 3 равно 954.
Выполняем письменное деление по алгоритму.
824 : 4 (аналогично 565 : 5, 234 : 8, 632 : 8, 434 : 7, 984 : 8)
1) Выделю первое неполное делимое, чтобы определить количество цифр в частном. Первое неполное делимое – 8 сот. высший разряд – сотни, значит, в частном 3 знака.
2) Нахожу цифру сотен в частном: 8 сот : 4 = 2 сот.
3) Нахожу, сколько сотен разделили: 2сот. · 4 = 8 сот.
4) Нахожу, сколько сотен осталось разделить: 8 сот. – 8 сот. = 0 сот., 0 сот. < 4, значит, в частном 2 сотни.
5) Образую второе неполное делимое: 0 сот. – это 0 дес. да еще 2 дес. – 2 дес.
6) Нахожу, количество десятков в частном: 2 дес. : 4 = 0 дес.
7) Нахожу, сколько десятков разделили: 0 дес. · 4 = 0 дес.
8) Нахожу, сколько десятков осталось разделить: 2 дес. – 0 дес. = 2 дес., 2 дес < 4, значит, в частном 0 десятков.
9) Образую третье неполное делимое: 2 дес. – это 20 ед. да еще 4 ед. – 24 ед.
10) Нахожу количество единиц в частном: 24 ед. : 4 = 6 ед.
11) Нахожу, сколько единиц разделили: 6 ед. · 4 = 24 ед.
12) Нахожу, сколько единиц осталось разделить: 24 ед. – 24 ед. = 0 ед., 0 ед. < 4, значит, в частном 6 единиц.
13) Читаю ответ. Значение частного от деления 824 на 4 равно 206.
Оформляем задание в тетрадь.
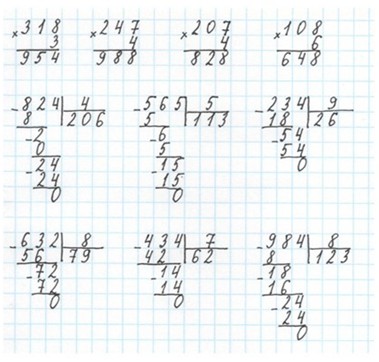
Номер 8.
Запиши выражения и найди их значения.
1) Сумму чисел 960 и 40 уменьшить в 10 раз. 2) Частное чисел 500 и 100 увеличить на 25.
Ответ:
Помним о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Сумма – сложение – знак плюс.
Частное – деление – знак :
«Уменьшить в 10 раз», значит, разделить на 10.
«увеличить на 25», т.е. прибавить 25.
Вычисление значений выражения сводится к применению правил:
Правило прибавления числа к сумме:
(а + в) + с = (а + с) + в.
Правило прибавления суммы к числу:
а + (в + с) = (а + в) + с.
Записываем выражения.
1) (960 + 40) : 10
2) (500 : 100) + 25
Находим значения выражений.
1) (960 + 40) : 10 = 100
1) 960 + 40 = (900 + 60) + 40 = 900 + (60 + 40) = 900 + 100 = 1000, по прибавления числа к сумме.
2) 1000 : 10 = 100
2) (500 : 100) + 25 = 30
1) 500 : 100 = 5
2) 5 + 25 = 5 + (20 + 5) = 20 + (5 + 5) = 20 + 10 = 30, по правилу прибавления суммы к числу.
Номер 9.
На поездку в магазин и обратно мальчик затратил 1 ч 10 мин. Туда он ехал на велосипеде 25 мин, в магазине пробыл 15 мин. Сколько минут мальчик ехал обратно?
Ответ:
1 ч 10 мин = 70 мин
1) 25 + 15 = 40 (мин) – время, которое мальчик ехал и пробыл в магазине.
2) 70 − 40 = 30 (мин)
Ответ: 30 минут он ехал обратно.
Помним о соотношении частей и целого:
часть + часть = целое
целое – 1часть = 2часть
целое – 2часть = 1часть
Оформляем условие в виде схематического рисунка.
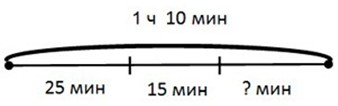
Рассуждаем.
Поездка в магазин состоит из 3 этапов: дорога до магазина, время в магазине, дорога до дома.
Чтобы узнать, сколько времени мальчик потратил, нужно сложить количество времени в пути и в магазине.
1 ч 10 мин = 70 мин.
1) 25 + 15 = 40(мин) – время, которое мальчик ехал и пробыл в магазине.
Продолжаем рассуждение.
Общее количество времени в магазине складывается из количества времени, проведенного в пути, времени в магазине и обратно. Значит, чтобы узнать, сколько времени потратил мальчик на дорогу обратно, нужно из общего количества времени вычесть количество времени в пути и магазине.
2) 70 − 40 = 30 (мин).
Записываем ответ.
Ответ: 30 минут он ехал обратно.
Решение выражением: 70 – (25 + 15) = 30 (мин).
Номер 10.
Из 28 м ткани сшили 7 одинаковых платьев. Сколько потребуется ткани, чтобы сшить 12 таких платьев? Сколько таких платьев можно сшить из 60 м ткани?
Ответ:
1) 28 : 7 = 4 (м) – для пошива одного платья.
2) 4 ∙ 12 = 48 (м) – для пошива 12 платьев.
3) 60 : 4 = 15 (пл.) – можно сшить из 60 м ткани.
Ответ: 48 м ткани нужно на пошив 12 платьев; 15 платьев всего можно сшить из 60 м ткани.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помни о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Расход ткани на 1 платье · кол-во платьев = общий расход ткани.
Общий расход ткани : кол-во платьев = расход ткани на 1 платье.
Общий расход ткани : расход ткани на 1 платьев = кол-во платьев.
Оформляем условие в виде таблицы.

Из 27 метров ткани сшили 7 одинаковых платьев. Значит, нам известно общее количество ткани и количество платьев, а расход ткани на 1 платьев – неизвестно.
Рассуждаем.
Из таблицы к задаче видно, что общее количество ткани складывается из количества ткани, расходуемой на каждое платье.
Чтобы узнать сколько метров ткани тратится на 1 платье, нужно общее количество платьев разделить на количество платьев.
1) 28 : 7 = 4 (м) – для пошива одного платья.
Продолжаем рассуждение.
Из таблицы к задаче видно, что общее количество ткани складывается из количества ткани, расходуемой на каждое платье, при этом расход ткани на 1 платье одинаковый. Значит, чтобы узнать, сколько ткани расходуется на 12 платьев, нужно расход ткани на 1 платье умножить на количество платьев.
2) 4 ∙ 12 = 48 (м) – для пошива 12 платьев.
Продолжаем рассуждение.
Из таблицы к задаче видно, что общее количество ткани складывается из количества ткани, расходуемой на каждое платье. Поэтому, чтобы узнать, сколько платьев можно сшить из 60 метров ткани, нужно общее количество ткани разделить на расход ткани.
3) 60 : 4 = 15 (пл.) – можно сшить из 60 м ткани.
Записываем ответ.
Ответ: 48 м; 15 платьев.
Номер 11.
1) Выпиши названия всех многоугольников. 2) Найди периметр и площадь квадрата ABCD. 3) Сравни площадь прямоугольника AMKD и площадь треугольника ABC.

1) Четырехугольники: ABCD, AMKD, AOKD, MBCO, MBCK. Треугольники: ABC, ACD, COK, AMO. 2) Длина стороны квадрата ABCD равна 2 см. Периметр 2 ∙ 4 = 8 см. Площадь квадрата 2 ∙ 2 = 4 см2. 3) Площадь прямоугольника AMKD равна площади треугольника АВС, так как их площади составляют половину площади квадрата ABCD.
1) Многоугольник – геометрическая фигура, состоящая из некоторого количества углов и сторон.
2) Периметр фигуры – сумма длин всех ее сторон.
Квадрат – фигура, у которой все стороны равны, значит, периметр квадрата равна произведению длины стороны на количество сторон.
Площадь фигуры – часть плоскости, занятая фигурой. Чтобы вычислить площадь квадрата, нужно длину стороны умножить на ширину.
У квадрата все стороны равны, значит длину стороны умножаю на саму себя, чтобы вычислить площадь квадрата.
3) Чтобы сравнить площадь треугольника АВС и прямоугольника АМКD, нужно сначала вычислить их.
Площадь фигуры – часть плоскости, занятая фигурой. Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину. По схеме догадайся, чесу равна площадь треугольника АВС.
Рассуждаем.
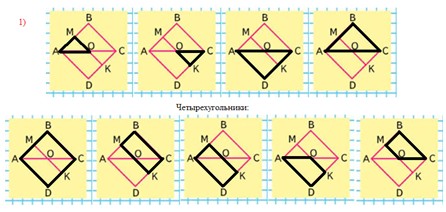
Четырехугольники: ABCD, AMKD, AOKD, MBCO, MBCK.
Треугольники: ABC, ACD, COK, AMO.
Найдём периметр и площадь квадрата.
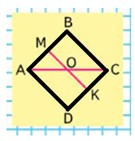
Длина стороны квадрата ABCD равна 2 см. Периметр 2 ∙ 4 = 8 см.
Площадь квадрата 2 ∙ 2 = 4 см2.
Сравним площадь прямоугольника AMKD и площадь треугольника ABC.
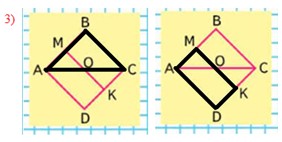
Площадь прямоугольника AMKD равна площади треугольника АВС, так как их площади составляют половину площади квадрата ABCD.
Задание на полях страницы.
Продолжи ряды чисел:
456 466 476 486 ... ... ... ... 540 530 520 510 ... ... ... ...
Ответ:Продолжение: ... 496, 506, 516, 526. ... 500, 490, 480, 470.
Чтобы продолжить ряды чисел, проанализируйте их: как они составлены, из каких чисел. Выявите закономерности и продолжите ряды.
Проанализируем ряд чисел.
Первый ряд: 456 , 466, 476, 486...
Каждое следующее число на 10 больше предыдущего, т.е. увеличивается на 10 единиц.
Продолжим числовой ряд.
486 + 10 = 496
496 + 10 = 506
506 + 10 = 516
516 + 10 = 526
Проанализируем ряд чисел.
Второй ряд: 540, 530, 520, 510...
Каждое следующее число на 10 меньше предыдущего, т.е. уменьшается на 10 единиц.
Продолжим числовой ряд.
510 – 10 = 500
500 – 10 = 490
490 – 10 = 480
480 – 10 = 470
Что узнали. Чему научились.
Номер 1.
Ответ:
Номер 2.
Ответ:

Номер 3.
Сравни числа.
Ответ:796 < 800 312 < 320 1000 > 999
Номер 4.
Ответ:
Номер 5.
Вычисли и проверь деление умножением.
Ответ:
Номер 6.
Ответ:
Номер 7.
Ответ:
Номер 8.
Запиши выражения и найди их значения.
1) Сумму чисел 960 и 40 уменьшить в 10 раз. 2) Частное чисел 500 и 100 увеличить на 25.
Ответ:
Номер 9.
На поездку в магазин и обратно мальчик затратил 1 ч 10 мин. Туда он ехал на велосипеде 25 мин, в магазине пробыл 15 мин. Сколько минут мальчик ехал обратно?
Ответ:
1 ч 10 мин = 70 мин
1) 25 + 15 = 40 (мин) – время, которое мальчик ехал и пробыл в магазине.
2) 70 − 40 = 30 (мин)
Ответ: 30 минут он ехал обратно.
Номер 10.
Из 28 м ткани сшили 7 одинаковых платьев. Сколько потребуется ткани, чтобы сшить 12 таких платьев? Сколько таких платьев можно сшить из 60 м ткани?
Ответ:
1) 28 : 7 = 4 (м) — для пошива одного платья.
2) 4 ∙ 12 = 48 (м) — для пошива 12 платьев.
3) 60 : 4 = 15 (пл.) — можно сшить из 60 м ткани.
Ответ: 48 м нужно для пошива 12 платьев; 15 платьев можно сшить из 60 м ткани.
Номер 11.
1) Выпиши названия всех многоугольников. 2) Найди периметр и площадь квадрата ABCD. 3) Сравни площадь прямоугольника AMKD и площадь треугольника ABC. Подтверди свой ответ.

1) Четырехугольники: ABCD, AMKD, AOKD, MBCO, MBCK.
Треугольники: ABC, ACD, COK, AMO.
2) Длина стороны квадрата ABCD равна 2 см.
Периметр 2 ∙ 4 = 8 см.
Площадь квадрата 2 ∙ 2 = 4 см2.
3) Площадь прямоугольника AMKD равна площади треугольника АВС, так как их площади составляют половину площади квадрата ABCD.
4 : 2 = 2 (см2) — площадь треугольника АВС;
2 ∙ 1 = 2 (см2) — площадь прямоугольника АМКD.
Задание на полях страницы
Продолжи ряды чисел:
456 466 476 486 ... ... ... ... 540 530 520 510 ... ... ... ...
Ответ:Продолжение: ... 496, 506, 516, 526. ... 500, 490, 480, 470.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.