Математика 4 класс учебник Моро, Бантова 1 часть ответы – страница 11

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Вспомни свойства умножения и объясни, почему верны равенства.
Ответ:Равенства верны, потому что от перестановки множителей произведение не меняется.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним, что существует такое свойство умножения, как переместительное, где а · в = в · а, т.е. от перестановки мест множителей, значение произведения не изменяется.
Проверим вычислением.
45 · 2 и 2 · 45
45 · 2 = 90, это по 45 – 2 раза, где 45 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
2 · 45 = 90, это по 2 – 45 раз, где 2 – одинаковое слагаемое, а 45 – количество одинаковых слагаемых.
3 · 328 и 328 · 3,
3 · 328 = 984, это по 3 – 328 раз, где 3 – одинаковое слагаемое, а 328 – количество одинаковых слагаемых.
328 · 3 = 984, это по 328 – 3 раза, где 328 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
5 · 123 = 123 · 5
5 · 123 = 615, это по 5 – 123 раза, где 5 – одинаковое слагаемое, а 123 – количество одинаковых слагаемых.
123 · 5 = 615, это по 123 – 5 раз, где 123 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
Делаем вывод.
Данные выражения равны по переместительному свойству умножения.
Номер 44.
Вычисли, применив перестановку множителей:
Ответ:
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним, что существует алгоритм объяснения умножения трехзначного числа на однозначное.
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
5) умножаю десятки;
6) умножаю сотни;
7) Умножение окончено. Читаю ответ.
Помним, что разряд должен быть записан под разрядом и что существует такое свойство умножения, как переместительное, где а · в = в · а, т.е. от перестановки мест множителей, значение произведения не изменяется.
Меняем множители местами и выполняем умножение по алгоритму.
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
1 ед. · 3 = 3 ед. 3 ед. < 10 ед., значит, записываю 3 единицы под единицами.
5) умножаю десятки; 6 дес. · 3 = 18 дес. – это 1 сот и 8 дес.,
значит, 8 дес. записываю под десятками, а 1 сот запоминаю.
6) умножаю сотни; 2сот. · 3 = 6 сот. да еще 1 сот. – 7 сот. 7 сот. < 10 сот., значит. 7 сотен записываю под сотнями.
7) Умножение окончено. Читаю ответ.
Значение произведения от умножения 261 на 3 равно 783.
Аналогично выполняем вычисление остальных выражений.

Номер 45.
Ответ:
а · в – значение произведения, вычисляется умножением.
с : d – значение частного, вычисляется делением.
Вспомним зависимость между компонентами и результатом действия умножения, деления:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Делимое : делитель = значение частного.
Делимое : значение частного = делитель.
Значение частного · делитель = делимое.
Находим значения выражений, применяя правила.
6 · 7 = 42, это по 6 – 7 раз, где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
20 : 5 = 4, потому что 5 · 4 = 20, это по 5 – 4 раза, где 5 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
48 : 8 = 6, потому что 8 · 6 = 48, это по 8 – 6 раз, где 8 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
9 : 9 = 1, потому что если любое число умножить на единицу, то получится это же число.
0 : 7 = 0, потому что если любое число умножить на 0, то получится 0.
0 · 5 = 0, потому что если 0 умножить на любое число, то получится 0.
45 : 5 = 9, потому что 5 · 9 = 45, это по 5 – 9 раз, где 5 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
4 · 9 = 36, это по 4 – 9 раз, где 4 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
24 : 8 = 3, потому что 8 · 3 = 24, это по 8 – 3 раза, где 8 – одинаковое слагаемое, а 3 – количество одинаковых слагаемых.
21 : 21 = 1, потому что если любое число разделить на само себя, то получится единица.
18 : 18 = 1, потому что если любое число разделить на само себя, то получится единица.
0 : 7 = 0, потому что если 0 разделить на любое число, то получится 0.
Заполняем таблицу.
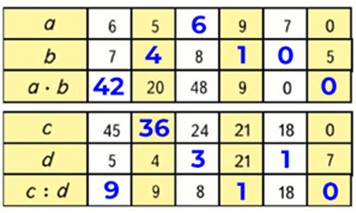
Номер 46.
Объясни записи на полях. Вычисли.

Произведение любого числа и числа 0 даёт число 0.
Произведение любого числа и 1 даёт само это число.
304 ∙ 3 = 3 ∙ 304 = 3 ∙ (300 + 4) = 900 + 12 = 912
481 ∙ 2 = 2 ∙ 481 = 2 ∙ 400 + 2 ∙ 80 + 2 ∙ 1 = 800 + 160 + 2 = 962
207 ∙ 4 = 200 ∙ 4 + 7 ∙ 4 = 800 + 28 = 828
116 ∙ 5 = 100 ∙ 5 + 10 ∙ 5 + 6 ∙ 5 = 500 + 50 + 30 = 580
Или можно оформить умножение в столбик:

Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним алгоритм объяснения умножения трехзначного числа на однозначное. Следуй ему:
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
5) умножаю десятки;
6) умножаю сотни;
7) Умножение окончено. Читаю ответ.
Помним, что разряд должен быть записан под разрядом и что существует такое свойство умножения, как переместительное, где а · в = в · а, т.е. от перестановки мест множителей, значение произведения не изменяется.
Помним о частных случаях умножения. Один из них – умножение на единицу (а · 1). При умножении любого числа на 1, получается число, которое умножали. Существует еще и другие: умножение числа на 0 (а · 0) , и 0 на любое число (0 · а).
Также существует правила прибавления любого числа к нулю (0 + а), вычитания нуля из любого числа (а – о) и вычитания из числа этого числа (а – а).
Объясняем записи.
c · 0 = 0 и b · 0 = 0
Произведение любого числа и числа 0 даёт число 0.
1 · k = k и d · 1 = d
Произведение любого числа и 1 даёт само это число.
Выполним вычисления разложив на удобные множители.
304 ∙ 3 = 3 ∙ 304 = 3 ∙ (300 + 4) = 900 + 12 = 912
481 ∙ 2 = 2 ∙ 481 = 2 ∙ 400 + 2 ∙ 80 + 2 ∙ 1 = 800 + 160 + 2 = 962
207 ∙ 4 = 200 ∙ 4 + 7 ∙ 4 = 800 + 28 = 828
116 ∙ 5 = 100 ∙ 5 + 10 ∙ 5 + 6 ∙ 5 = 500 + 50 + 30 = 580
Делаем вывод
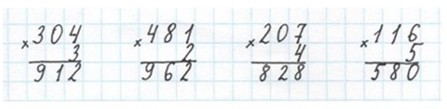
Номер 47.
Вася купил 4 марки, по 10 р. каждая. Найди стоимость этих марок Составь и реши две задачи, обратные данной.
Ответ:
10 ∙ 4 = 40 (руб.)
Ответ: 40 рублей стоят марки.
Обратная задача 1:
Вася за 4 марки заплатил 40 рублей. Сколько рублей стоит одна марка?

40 : 4 = 10 (руб.)
Ответ: 10 рублей стоит одна марка.
Обратная задача 2:
Вася заплатил за марки 40 рублей. Сколько он купил марок, если одна марка стоит 10 рублей?

40 : 10 = 4 (м.) Ответ: 4 марки купил Вася.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним о зависимости между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Цена марки · количество марок = общая стоимость марок.
Общая стоимость марок : кол-во марок = цена марки.
Обща стоимость марок : цена марки = кол-во марок.
Для того чтобы составить и решить обратную задачу, необходимо известное сделать неизвестным и наоборот.
Оформляем условие в виде таблицы.

Вася купил 4 марки по 10 рублей каждая. Нам известно количество марок и цена, а стоимость всех марок – нет.
Рассуждаем.
Общая стоимость марок складывается из стоимости каждой из марок. Значит, чтобы узнать, сколько стоят все марки, нужно цену марки умножаю на количество марок. Вычисляется умножением.
10 ∙ 4 = 40 (руб.)
Записываем ответ.
Ответ: 40 рублей стоят марки.
Составляем и решаем 1 обратную задачу.

Вася за 4 марки заплатил 40 рублей. Значит, нам известно количество марок и общая стоимость, а цена марки – нет.
40 : 4 = 10 (руб.)
Ответ: 10 рублей стоит одна марка.
Составляем и решаем 2 обратную задачу.

Вася заплатил за все марки 40 рублей, одна стоит 10 рублей. Значит, нам известна общая стоимость марок и цена марки, а их количество нет.
40 : 10 = 4 (м.)
Ответ: 4 марки купил Вася.
Номер 48.
Каким действием можно узнать стоимость покупки, если известны цена и количество купленных предметов? Составь и реши задачу на нахождение стоимости; задачу на нахождение цены.
Ответ:Стоимость покупки равна произведению цены и количества купленных предметов.
Задача 1:
Миша купил 6 мячей по цене 35 рублей за мяч. Сколько денег Миша потратил на всю покупку?
35 ∙ 6 = 210 (руб.)
Ответ: 210 рублей стоимость покупки.
Задача 2:
За 3 кг яблок мама заплатила 186 рублей. Сколько стоит один килограмм яблок?
186 : 3 = 62 (руб.)
Ответ: 62 рубля цена яблок.
Помним конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением, где а · 3, а – первый множитель, а 3 – количество множителей.
Помним зависимость между компонентами и результатом действия умножения:
1 множитель · 2 множитель = значение произведения.
Значение произведения : 1 множитель = 2 множитель.
Значение произведения : 2 множитель = 1 множитель.
Данная задача характеризуется зависимостями между компонентами:
Цена предмета · количество предметов = общая стоимость предметов.
Общая стоимость предметов : количество предметов = цена предмета.
Общая стоимость предметов : цена предмета = количество предметов.
Условие оформляем в вид таблицы.
Шаг 1.
Составляем 1 задачу и оформляем условие.
Миша купил 6 мячей по цене 35 рублей за мяч. Значит, нам известная цена мяча и их количество, а общая стоимость – неизвестное.

Рассуждаем.
Чтобы узнать, чему равна общая стоимость покупки, нужно цену мяча умножить на их количество.
35 ∙ 6 = 210 (руб.)
Записываем ответ.
Ответ: 210 рублей стоимость покупки.
Шаг 1.
Составляем 2 задачу и оформляем условие.
За 3 кг яблок мама заплатила 186 рублей. Значит, нам известно количество кг яблок и общая стоимость, а цена килограмма – нет.

Рассуждаем.
Чтобы узнать, сколько стоит 1 кг яблок, нужно общую стоимость яблок разделить на количество купленных.
186 : 3 = 62 (руб.)
Записываем ответ.
Ответ: 62 рубля цена яблок.
Номер 49.
Купили 30 кг белой краски, а синей – в 7 раз больше. на сколько больше килограммов купили синей краски, чем белой?
Ответ:
1) 30 ∙ 7 = 210 (кг) – синей краски.
2) 210 – 30 = 180 (кг)
Ответ: на 180 кг синей краски больше, чем белой.
Условие оформляем краткой записью.
Задача решается в два действия.
«в 7 раз больше»: значение находим умножением.
«на сколько больше»: из большего числа вычесть меньшее число, с помощью знака «-».
Оформляем условие.
Известно, что белой краски – 30 кг, а синей – неизвестно, но в 7 раз больше, чем белой.
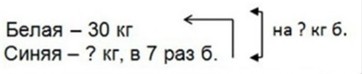
Рассуждаем.
Чтобы узнать, сколько синей краски, нужно количество белой краски умножить на 7. Выполняем действие умножение.
30 · 7 = 210 (кг) – синей.
Рассуждаем.
Чтобы узнать, на сколько синей краски больше, чем белой, нужно из количества синей краски вычесть количество белой. Выполняем действие вычитание.
210 – 30 = 180 (кг)
Записываем ответ.
Ответ: на 180 кг синей краски больше.
Решение выражением: 30 · 7 – 30 = 180 (кг)
Номер 50.
Начерти прямоугольник, ширина которого 2 см, а длина в 3 раза больше. На сколько сантиметров длина этого прямоугольник больше его ширины?
Ответ:
1) 2 ∙ 3 = 6 (см) – длина прямоугольника.
2) 6 – 2 = 4 (см)
Ответ: на 4 см длина прямоугольника больше ширины.
Чертим прямоугольник со сторонами 2 см и 6 см.

Условие оформляем краткой записью.
Задача решается в два действия.
«в 3 раза больше», значит, вычисляется умножением.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Вычисляется вычитанием.
Оформляем условие в виде краткой записи.

Рассуждаем.
Ширина прямоугольника равна 2 см, а длина в 3 раза больше. Значит, чтобы узнать, чему равна длина прямоугольника, нужно ширину прямоугольника умножить на 3.
1) 2 ∙ 3 = 6 (см) – длина прямоугольника.
Продолжаем рассуждение.
Мы узнали, что длина прямоугольника – 6 см, а ширина – 2 см. Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее. Значит, чтобы узнать, на сколько длина прямоугольника больше ширины, нужно из значения длины вычесть значение ширины.
2) 6 − 2 = 4 (см)
Записываем ответ.
Ответ: на 4 см длина больше ширины.
Решение в виде выражения: (2 · 3) – 2 = 4 см
Номер 51.
Сравни площади прямоугольников ABCD и MNOP, MNOP и EFTK.

SABCD – 2 ∙ 3 = 6 см2
SMNOP – 1 ∙ 2 = 2 см2
Площадь прямоугольника ABCD больше площади прямоугольника MNOP на 4 см²
6 см2 − 2 см2 = 4 см2
SEFTK – 2 ∙ 2 = 4 см2
Площадь прямоугольника EFTK больше площади прямоугольника MNOP на 2 см²
6 см2 − 4 см2 = 2 см2
Площадь – часть плоскости, которую занимает фигура или это внутренняя часть какой-либо геометрической фигуры. Обычно обозначается латинской буквой S.
Площадь фигуры измеряется в квадратных единицах измерения (см2, мм2, дм2.).
У прямоугольника есть две величины, с помощью которых можно площадь прямоугольника вычислить – длина и ширина. Чтобы вычислить площадь прямоугольника, нужно длину умножить на ширину.
1 найти площадь каждой из фигур.
1) EFKT – квадрат.
S = ? см2
S = EF · FT
S = 2 см · 2 см = 4 см2
2) MNOP – прямоугольник.
S = ? см2
S = MN · NO
S = 1 см · 2 см = 2 см2
3) ABCD – прямоугольник.
S = ? см2
S = AB · BC
S = 3 см · 2 см = 6 см2
Сравним полученные площади.
Чтобы сравнить площади, нужно понять, на сколько они больше или меньше друг друга. Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
Площадь ABCD больше площади MNOP на 4 см2
6 см2 – 2 см2 = 4 см2
Площадь EFTK больше площади MNOP на 2 см2
6 см2 – см2 = 2 см2
Номер 52.
Ответ:
Помним алгоритм умножения трехзначного числа на однозначное:
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
5) умножаю десятки;
6) умножаю сотни;
7) Умножение окончено. Читаю ответ.
Помним алгоритм вычитания в столбик:
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда. Вычитаю единицы;
5) вычитаю десятки;
6) вычитаю сотни;
7) вычитание окончено. Читаю ответ.
Выполняем сложение по алгоритму.
651 + 126
1) записываю первое слагаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак плюс.
2) Записываю второе слагаемое так, чтобы разряд стоял под разрядом.
3) Провожу черту, обозначающую знак равно.
4) Сложение начинаю с единиц низшего разряда. 1 ед. + 6 ед. = 7 ед. 7 ед.<10 ед., значит, 7 единиц записываю под единицами.
5) Складываю десятки, 5 дес. + 2 дес. = 7 дес. 7 дес < 10 дес., значит, 7 десятков записываю под десятками.
6) Складываю сотни: 6 сот. + 1 сот. = 7 сот., 7 сот. < 10 сот., значит, 7 сотен записываю в разряд сотен.
7) Сложение окончено читаю ответ: значение суммы от сложения 651 и 126 равно 777.
ЗВыполняем вычитание по алгоритму.
379 – 253 (аналогично 306 – 138, 402 – 243)
1) записываю уменьшаемое так, чтобы каждая цифра стояла в своей клетке. Ставлю знак минус;
2) записываю вычитаемое так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) вычитание начинаю с единиц низшего разряда. Вычитаю единицы; 9 ед. – 3 ед. = 6 ед, 6 ед. < 10 ед., значит, 6 единиц записываю под единицами.
5) вычитаю десятки; 7 дес. – 5 дес. = 2 дес. 2 дес.<10 дес., значит, 2 десятка записываю в разряд десятков.
6) вычитаю сотни; 3 сот. – 2сот. = 1сот. 1 сот. < 10 сот, значит, 1 сотню записываю в разряд сотен.
7) вычитание окончено. Читаю ответ. Значение разности от вычитания 253 из 379 равно 126.
Выполняем умножение по алгоритму.
453 · 2 (аналогично 321 · 3, 5 · 171, 6 · 98)
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда; 3 ед. * 2 = 6 ед., 6 ед.< 10 ед., значит, 6 единиц записываю в разряд единиц.
5) умножаю десятки; 5 дес. * 2 = 10 дес., это 1 сот 0 дес., значит, 0 десятков записываю в разряд десятков, а 1 сотню запоминаю.
6) умножаю сотни; 4 сот. * 2 = 8 сот да еще 1 сот. – 9 сот., 9 сот < 10 сот, значит, 9 сотен записываю в разряд сотен.
7) Умножение окончено. Читаю ответ. Значение произведения от умножении 453 на 2 равно 906.
Оформляем задание в тетрадь.
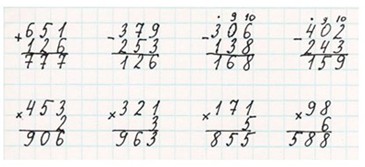
Номер 53.
Ответ:
Или можно оформить так:


Помним порядок выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Записываем выражения и расставляем порядок действий.
Выполняем вычисления и записываем ответ.
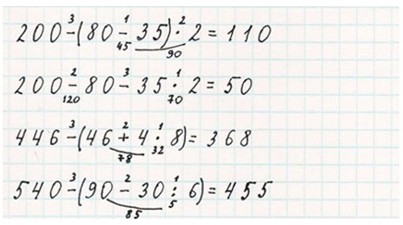
Вычисления можно оформить по действиям.

Задание внизу страницы.
Вычисли.
Ответ:
Помним алгоритм объяснения умножения трехзначного числа на однозначное:
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
5) умножаю десятки;
6) умножаю сотни;
7) Умножение окончено. Читаю ответ.
Помним, что разряд должен быть записан под разрядом.
Помним переместительное свойство, где а · в = в · а, т.е. от перестановки множителей, значение произведения не изменяется.
Выполняем вычисления по алгоритму.
196 · 3
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить;
2) записываю второй множитель так, чтобы разряд стоял под разрядом;
3) провожу черту, обозначающую знак равно.
4) умножение начинаю с единиц низшего разряда;
6 ед. · 3 = 18 ед. – это 1 дес. 8 ед. Значит, 8 ед. записываю под единицами, а 1 дес. запоминаю.
5) умножаю десятки; 9 дес. · 3 = 27 дес. да еще 1 дес. – 28 дес. – это 2 сот. 8 дес. Значит, 8 дес. записываю под десятками. а 2 сот запоминаю.
6) умножаю сотни; 1 сот. · 3 = 3 сот да еще 2 сот – 5 сот. 5 сот < 10 сот, значит, 5 сот записываю под сотнями.
7) Умножение окончено. Читаю ответ.
438 · 2
1) записываю первый множитель так, чтобы каждая цифра стояла в своей клетке. Ставлю знак умножить:
2) записываю второй множитель так, чтобы разряд стоял под разрядом,
3) провожу черту, обозначающую знак равно;
4) умножение начинаю с единиц низшего разряда;
8 ед. · 2 = 16 ед. – это 1 дес. 6 ед. Значит, 6 ед. записываю под единицами, а 1 дес. запоминаю.
5) умножаю десятки; 3 дес. · 2 = 6 дес, да еще 1 дес. – 7 дес. 7 дес. < 10 дес. Значит, 7 дес. записываю под десятками.
6) умножаю сотни; 4 сот. · 2 = 8 сот, 8 сот – 10 сот, значит, 8 сот записываю под сотнями.
7) Умножение окончено. Читаю ответ.
Оформляем задание в тетрадь.
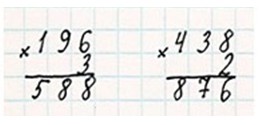
Делаем вывод.
Получаем, что 6сот.5дес. и 5ед. = 655.
Номер 45.
Вычисли.
3 ∙ 261 4 ∙ 187 5 ∙ 173 4 ∙ 247 2 ∙ 349
Ответ:
Номер 46.
Ответ:
Номер 47.
Объясни записи на полях. Вычисли.

Произведение любого числа и числа 0 даёт число 0.
Произведение любого числа и 1 даёт само это число.
304 ∙ 3 = 3 ∙ 304 = 3 ∙ (300 + 4) = 900 + 12 = 912
481 ∙ 2 = 2 ∙ 481 = 2 ∙ 400 + 2 ∙ 80 + 2 ∙ 1 = 800 + 160 + 2 = 962
207 ∙ 4 = 200 ∙ 4 + 7 ∙ 4 = 800 + 28 = 828
116 ∙ 5 = 100 ∙ 5 + 10 ∙ 5 + 6 ∙ 5 = 500 + 50 + 30 = 580
Или можно оформить умножение в столбик:

Номер 48.
Вася купил 4 марки, по 10 р. каждая. Найди стоимость этих марок Составь и реши две задачи, обратные данной.
Ответ:
10 ∙ 4 = 40 (руб.)
Ответ: 40 рублей стоят марки.
Обратная задача 1:
Вася за 4 марки заплатил 40 рублей. Сколько рублей стоит одна марка?

40 : 4 = 10 (руб.)
Ответ: 10 рублей стоит одна марка.
Обратная задача 2:
Вася заплатил за марки 40 рублей. Сколько он купил марок, если одна марка стоит 10 рублей?

40 : 10 = 4 (м.) Ответ: 4 марки купил Вася.
Номер 49.
Каким действием можно узнать стоимость покупки, если известны цена и количество купленных предметов? Составь и реши задачу на нахождение стоимости; задачу на нахождение цены.
Ответ:Стоимость покупки равна произведению цены и количества купленных предметов.
Задача 1:
Миша купил 6 мячей по цене 35 рублей за мяч. Сколько денег Миша потратил на всю покупку?
35 ∙ 6 = 210 (руб.)
Ответ: 210 рублей стоимость покупки.
Задача 2:
За 3 кг яблок мама заплатила 186 рублей. Сколько стоит один килограмм яблок?
186 : 3 = 62 (руб.)
Ответ: 62 рубля цена яблок.
Номер 50.
Купили 30 кг белой краски, а синей – в 7 раз больше. на сколько больше килограммов купили синей краски, чем белой?
Ответ:
1) 30 ∙ 7 = 210 (кг) – синей краски.
2) 210 – 30 = 180 (кг)
Ответ: на 180 кг синей краски больше, чем белой.
Номер 51.
Начерти прямоугольник, ширина которого 2 см, а длина в 3 раза больше. На сколько сантиметров длина этого прямоугольник больше его ширины?
Ответ:
1) 2 ∙ 3 = 6 (см) – длина прямоугольника.
2) 6 – 2 = 4 (см)
Ответ: на 4 см длина прямоугольника больше ширины.
Чертим прямоугольник со сторонами 2 см и 6 см.

Номер 52.
Сравни площади прямоугольников ABCD и MNOP, MNOP и EFTK. У какой фигуры 4 оси симметрии?

SABCD – 2 ∙ 3 = 6 см2
SMNOP – 1 ∙ 2 = 2 см2
Площадь прямоугольника ABCD больше площади прямоугольника MNOP на 4 см²
6 см2 − 2 см2 = 4 см2
SEFTK – 2 ∙ 2 = 4 см2
Площадь прямоугольника EFTK больше площади прямоугольника MNOP на 2 см²
6 см2 − 4 см2 = 2 см2
4 оси симметрии имеет фигура EFTK, так как это квадрат.
Номер 53.
Ответ:
Номер 54.
Ответ:
Или можно оформить так:


Задание внизу страницы
Вычисли.
Ответ:
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.