Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 66

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Приемы устных вычислений
Номер 1.
Вычисли с устным объяснением:
Ответ:300 – 200 = 100 (3 сот. − 2 сот. = 1 сот.)
900 + 100 = 1000 (9 сот. + 1 сот. = 10 сот.)
400 – 300 = 100 (4 сот. − 3 сот. = 1 сот.)
800 – 500 = 300 (8 сот. − 5 сот. = 3 сот.)
90 + 80 = 170 (9 дес. + 8 дес. = 17 дес.)
60 + 70 = 130 (6 дес. + 7 дес. = 13 дес.)
160 – 70 = 90 (16 дес. − 7 дес. = 9 дес.)
150 – 90 = 60 (15 дес. − 9 дес. = 6 дес.)
Помни, что при сложении и вычитании чисел, запись которых оканчивается нулями, всегда можно заменить их действиями с сотнями и десятками.
Выполняем вычисления с пояснениями.
300 − 200 = 3 сот. − 2 сот. = 1 сот. = 100
Из 3 сотен вычесть 2 сотни получится 1 сотня, так как 3 − 2 = 1.
900 + 100 = 9 сот. + 1 сот. = 10 сот. = 1000
К 9 сотням прибавить 1 сотню получится 10 сотен, так как 9 + 1 = 10.
400 − 300 = 4 сот. − 3 сот. = 1 сот. = 100
Из 4 сотен вычесть 3 сотни получится 1 сотня, так как 4 − 3 = 1.
800 − 500 = 8 сот. − 5 сот. = 3 сот. = 300
Из 8 сотен вычесть 5 сотен получится 3 сотни, так как 8 − 5 = 3.
90 + 80 = 9 дес. + 8 дес. = 17 дес. = 170
К 9 десяткам прибавить 8 десятков получится 17 десятков, так как 9 + 8 = 17.
60 + 70 = 6 дес. + 7 дес. = 13 дес. = 130
К 6 десяткам прибавить 7 десятков получится 13 десятков, так как 6 + 7 = 13.
160 − 70 = 16 дес. − 7 дес. = 9 дес. = 90
Из 16 десятков вычесть 7 десятков получится 9 десятков, так как 16 − 7 = 9.
150 − 90 = 60, так как 15 дес. − 9 дес. = 6 дес.
Из 17 десятков вычесть 9 десятков получится 6 десятков, так как 15 − 9 = 6.
Оформляем задание в тетрадь.
300 − 200 = 100, так как 3 сот. + 2 сот. = 1 сот.
900 + 100 = 1000, так как 9 сот. + 1 сот = 10 сот.
400 − 300 = 100, так как 4 сот. − 3 сот. = 1 сот.
800 − 500 = 300, так как 8 сот. − 5 сот. = 3 сот.
90 + 80 = 170, так как 9 дес. + 8 дес. = 17 дес.
60 + 70 = 130, так как 6 дес. + 7 дес. = 13 дес.
160 − 70 = 90, так как 16 дес. − 7 дес. = 9 дес.
150 − 90 = 60, так как 15 дес. − 9 дес. = 6 дес.
Номер 2.
Витя купил 400 г сыра и на 100 г больше масла. Найди массу этой покупки.
Ответ:
1) 400 + 100 = 500 (г) – масла купил Витя. 2) 400 + 500 = 900 (г) – масса покупки. Ответ: масса этой покупки составляет 900 граммов.
1) «На 100 г больше» – это значит столько же, но плюс ещё 100 г.
2) Помни, что 100 = 1 сот.
Оформляем условие в виде краткой записи.
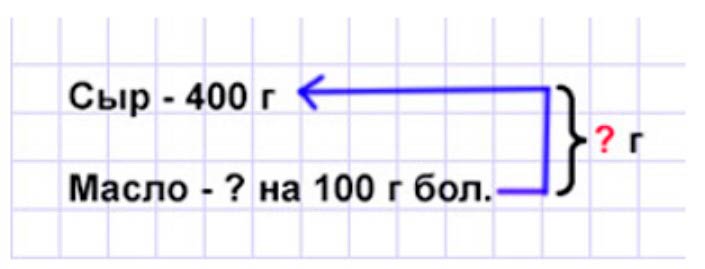
Рассуждаем.
Чтобы узнать сколько купили масла нужно к массе сыра прибавить 100 г.
400 + 100 = 4 сот. + 1 сот. = 5 сот. = 500 (г) – купили масла
Продолжаем рассуждение.
Общая масса покупки состоит из массы сыра и молока, сложим их.
500 + 400 = 5 сот. + 4 сот. = 9 сот. = 900 (г) – масса всей покупки.
Записываем ответ.
Ответ: 900 г.
Решение выражением:
400 + (500 + 400) = 900 (г) – масса всей покупки,
где 500 + 400 = масса масла.
Номер 3.
Ответ:308 см = 3 м 8 см 3 м 70 см = 370 см 45 мм = 4 см 5 мм 15 дм 8 см = 158 см
Помни, что 1 м = 10 см; 1 дм = 10 см, 1 см = 10 мм.
Выполняем вычисления с пояснениями.
308 см = 300 см + 8 см = 3 ∙ 100 см + 8 см = 3 м 8 см,
так как 1 м = 100 см;
45 мм = 40 мм + 5 мм = 4 ∙ 1 см + 5 мм = 4 см 5 мм,
так как 10 мм = 1 см;
3 м 70 см = 3 ∙ 100 см + 70 см = 300 см + 70 см = 370 см,
так как 1 м = 100 см;
15 дм 8 см = 15 ∙ 10 см + 8 см = 150 см + 8 см = 158 см,
так как 1 м = 10 см.
Оформляем задание в тетрадь.
308 см = 3 м 8 см
45 мм = 4 см 5 мм
3 м 70 см = 370 см
15 дм 8 см = 158 см
Номер 4.

По выражению 4 + 3 ∙ 5 ученик составил задачу: «У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у этих девочек вместе. Сколько денег у Коли?» Правильно ли составлена задача?
Ответ:Неправильно. Правильная задача: У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у Иры. Сколько денег было у Кати и Коли вместе?

4 + 3 · 5 = 19 (р) Ответ: 19 рублей у Коли и Кати вместе.
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) «в 5 раз больше» – вычисляется умножением.
Оформляем условие в виде краткой записи.
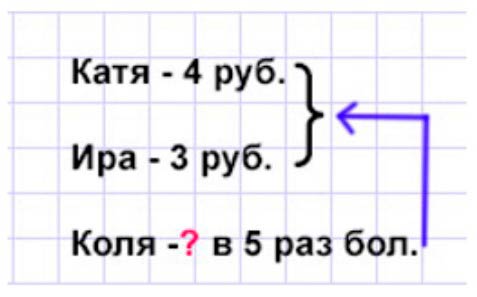
Рассуждаем.
Общее количество денег у девочек складывается из денег у Кати и Иры.
4 + 3 = 7 (руб.) – денег у Кати и Иры вместе.
Продолжаем рассуждение.
У Коли денег в 5 раз больше, это значит, что количество денег у девочек нужно сложить 5 раз. Но сложение одинаковых слагаемых можно заменить умножением.
7 ∙ 5 = 35 (руб.) – денег у Коли.
Записываем ответ.
Ответ: 35 рублей.
Решение выражением:
(4 + 3) ∙ 5 = 7 ∙ 5 = 35 (р.) – денег у Коли,
где 4 + 3 – общее количество денег у девочек.
Рассуждаем.
Первым действием количество денег увеличили в 5 раз, таким образом нашли количество денег у Коли.
5 ∙ 3 = 15 (р.) – денег у Коли.
Продолжаем рассуждение.
Вторым действием к количеству денег у Коли прибавили количество денег у Кати и узнали сколько денег у них вместе.
15 + 4 = 19 (р.) – денег у Коли и Кати вместе.
Записываем ответ.
Ответ: 19 рублей.
Решение выражением:
4 + 3 ∙ 5 = 19 (р.) – денег у Коли и Кати вместе,
где 3 ∙ 5 – количество денег у Коли.
Рассуждаем.
По выражению 4 + 3 ∙ 5, согласно порядку действий, мы узнаем общее количество денег у Коли и Кати, где денег у Коли в 5 раз больше, чем у Иры.
А по задаче, составленной учеником, мы узнаем сколько денег у Коли, при чём у него денег в 5 раз больше, чем у девочек вместе.
Выражение для решения задачи: (4 + 3) ∙ 5.
Значит, задача составлена неправильно.
Записываем ответ.
Ответ: задача составлена неправильно.
По выражению 4 + 3 · 5 ученик составил задачу: «У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у этих девочек вместе. Сколько денег у Коли?» Правильно ли составлена задача? Если нет, предложи свои способы внести исправления. Сколько способов получилось найти?
Ответ:Нет, задача составлена неправильно. 2 способа внести исправления:
1-й способ решения: Исправить текст задачи. Задача: У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у Иры. Сколько денег у Кати и Коли вместе?»

4 + 3 · 5 = 4 + 15 = 19 (р.) - всего Ответ: 19 рублей у Кати и Коли вместе.
2-й способ решения: Исправить выражение к задаче. Задача: «У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у этих девочек вместе. Сколько денег у Коли?»

(4 + 3) · 5 = 7 · 5 = 35 (р.) рублей Ответ: у Коли всего 35 рублей.
1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) «в 5 раз больше» – вычисляется умножением.
Рассмотрим задачу, которую составил ученик.
По выражению 4 + 3 ∙ 5 ученик составил задачу:
«У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у этих девочек вместе. Сколько денег у Коли?»
Решим эту задачу, составим по ней выражение и сравним с исходным выражением.
Оформляем условие в виде краткой записи.
-(2024).jpg)
Рассуждаем.
Общее количество денег у девочек складывается из денег у Кати и Иры.
4 + 3 = 7 (руб.) – у Кати и Иры вместе.
Продолжаем рассуждение.
У Коли денег в 5 раз больше, чем у девочек вместе. Тогда, чтобы найти сумму денег у Коли, нужно количество денег у девочек умножить на 5.
7 ∙ 5 = 35 (руб.) – у Коли.
Записываем ответ.
Ответ: у Коли 35 рублей.
Решение выражением: (4 + 3) ∙ 5 = 7 ∙ 5 = 35 (р.) – у Коли, где 4 + 3 – общее количество денег у девочек.
Делаем вывод.
Исходное выражение: 4 + 3 ∙ 5
Выражение по задаче: (4 + 3) ∙ 5
Значит, задача составлена неправильно.
В данном случае можно внести исправления в исходное выражение – поставить скобки.
Составим задачу.
По исходному выражению 4 + 3 ∙ 5 внесём исправления в задачу:
«У Кати 4 р., у Иры 3 р., а у Коли в 5 раз больше, чем у Иры. Сколько денег у Кати и Коли вместе?»
Решим эту задачу и проверим, верны ли исправления.
Оформляем условие в виде краткой записи.
-(2024).jpg)
Рассуждаем.
Чтобы узнать, сколько денег у Коли, нужно количество денег у Иры умножить на 5.
3 ∙ 5 = 15 (р.) – у Коли.
Продолжаем рассуждение.
Чтобы узнать, сколько денег у Кати и Коли вместе, нужно сложить деньги Кати и деньги Коли.
4 + 15 = 19 (р.) – у Коли и Кати вместе.
Записываем ответ.
Ответ: у Кати и Коли вместе 19 рублей.
Решение выражением: 4 + 3 ∙ 5 = 19 (р.) – у Коли и Кати вместе, где 3 ∙ 5 – количество денег у Коли.
Делаем вывод.
Исходное выражение: 4 + 3 ∙ 5
Выражение по задаче: 4 + 3 ∙ 5
Значит, исправления в задачу внесены верно.
Номер 5.
Выпиши уравнения, которые решаются делением, и реши их:
Ответ:x ∙ 7 = 14
х = 14 : 7
х = 2
Проверка:
2 ∙ 7 = 14
14 = 14
16 ∙ х = 64 19 ∙ х = 19
х = 64 : 16 х = 19 : 19
х = 4 x = 1
Проверка: Проверка:
16 ∙ 4 = 64 19 ∙ 1 = 19
64 = 64 19 = 19
75 : х = 5 19 : х = 1
х = 75 : 5 х = 19 : 1
х = 15 х = 19
Проверка: Проверка:
75 : 15 = 5 19 : 19 = 1
5 = 5 1 = 1
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Делением можно найти неизвестный делитель, неизвестное частное и неизвестный множитель.
Рассмотрим уравнения.
х : 7 = 14
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
Уравнение решается умножением.
x ∙ 7 = 14
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Уравнение решается делением.
16 ∙ x = 64
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Уравнение решается делением.
44 + х = 88
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
Уравнение решается сложением.
75 : x = 5
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно значение делимого разделить на значение частного.
Уравнение решается делением.
75 – х = 5
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность.
Уравнение решается вычитанием.
19 ∙ x = 19
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Уравнение решается делением.
19 : x = 1
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно значение делимого разделить на значение частного.
Уравнение решается делением.
Решим уравнения.
x ∙ 7 = 14
x = 14 : 7
x = 2
16 ∙ x = 64
x = 64 : 16
x = 4
75 : x = 5
x = 75 : 5
75 : 5 = (50 + 25) : 5 = 10 + 5 = 15
x = 15
19 ∙ x = 19
x = 19 : 19
x = 1
19 : x = 1
x = 19 : 1
x = 19
Сделаем проверку.
Для проверки решения уравнения, нужно вместо неизвестного подставить решение уравнения, то есть число которое получили.
Если правая и левая часть равенства равны, то уравнение решено верно.
x ∙ 7 = 14
Проверка: вместо х подставим число 2.
2 ∙ 7 = 14
14 = 14 – верно.
16 ∙ x = 64
Проверка: вместо х подставим число 4.
16 ∙ 4 = (10 + 6) ∙ 4 = 40 + 24 = 64
64 = 64 – верно.
75 : x = 5
Проверка: вместо х подставим число 15
75 : 15 = 5 – методом подбора.
5 = 5 – верно.
19 ∙ x = 19
Проверка: вместо х подставим число 1.
19 ∙ 1 = 19
19 = 19 – верно.
19 : x = 1
Проверка: вместо х подставим число 1.
19 : 1 = 19
19 = 19 – верно.
Номер 6.
Ответ:200 ∙ 4 + 200 = 200 * 5 = 1000
900 – 400 : 2 = 900 - 200 = 700
1000 : 2 + 500 = 500 + 500 = 1000
1000 : 5 – 200 = 200 - 200 = 0
300 : 300 = 1
300 – 300 = 0
1) Помни о порядке выполнения арифметических действий: сначала выполняются действия в скобках, затем умножение или деление, а потом – сложение или вычитание. Слева направо.
2) Помни, что при сложении и вычитании чисел, запись которых оканчивается нулями, можно заменить их действиями с сотнями и десятками.
Рассуждаем и выполняем вычисления по действиям.
200 ∙ 4 + 200 = 1000
1) 200 ∙ 4 = 2 сот. ∙ 4 = 8 сот. = 800
2) 800 + 200 = 8 сот. + 2 сот. = 10 сот. = 1000
900 − 400 : 2 = 700
1) 400 : 2 = 4 сот. : 2 = 2 сот. = 200
2) 900 − 200 = 9 сот. – 2 сот. = 7 сот. = 700
1 000 : 2 + 500 = 1000
1) 1000 : 2 = 10 сот. : 2 = 5 сот. = 500
2) 500 + 500 = 5 сот. + 5 сот. = 10 сот. = 1000
1 000 : 5 − 200 = 0
1) 1000 : 5 = 10 сот. : 5 = 2 сот. = 200
2) 200 − 200 = 2 сот. – 2 сот. = 0
300 : 300 = 3 сот. : 3 сот. = 1
Если число разделить на само себя, то получится один.
300 − 300 = 0
Если из числа вычесть само число, то получится нуль.
Оформляем задание в тетрадь.
200 ∙ 4 + 200 = 800 + 200 = 1000
900 − 400 : 2 = 900 − 200 = 700
1 000 : 2 + 500 = 500 + 500 = 1000
1 000 : 5 − 200 = 200 − 200 = 0
300 : 300 = 1
300 − 300 = 0
Номер 7.
4 карандаша и 3 тетради стоят 54 р., а 2 карандаша и 2 тетради – 34 р. Сколько стоят 6 таких карандашей и 5 таких тетрадей?
Ответ:4 к. + 3 т. = 54 р. 2 к. + 2 т. = 34 р. 6 к. + 5 т. = ? р. 54 + 34 = 88 (р.) – стоят 6 карандашей и 5 тетрадей. Ответ: 88 р стоят вместе 6 карандашей и 5 тетрадей.
Внимательно прочитай задачу и обрати внимание, сколько стоит общее число карандашей и тетрадей.
Оформляем условие в виде краткой записи.
4 кар. + 3 тет. = 54 р.
2 кар. + 2 тет. = 34 р.
6 кар. + 5 тет. = ?
Рассуждаем.
Внимательно рассмотрим условие задачи.
В условии задачи вначале говорится о 4 карандашах, а потом о 2 карандашах. Значит, всего 6 карандашей.
В условии задачи вначале говорится о 3 тетрадях, а потом о 2 тетрадях. Значит, всего 5 тетрадей.
Нам нужно узнать, сколько стоят 6 таких карандашей и 5 тетрадей. Значит, нужно эти две стоимости сложить.
4 кар. + 3 тет. + 2 кар. + 2 тет. = 6 кар. + 5 тет.
54 р. + 34 р. = 88 р. – стоят 6 карандашей и 5 тетрадей.
Записываем ответ.
Ответ: 88 рублей.
Задание внизу страницы
Вычисли.
Ответ:400 + 300 = 700 900 − 200 = 700 840 − 60 = 780
Помни, что при сложении и вычитании чисел, запись которых оканчивается нулями, можно заменить их действиями с сотнями и десятками.
Выполняем вычисления с пояснениями.
400 + 300 = 4 сот. + 3 сот. = 7 сот. = 700.
К 4 сотням прибавить 3 сотни получится 7 сотен.
900 − 200 = 9 сот. − 2 сот. = 7 сот. = 700.
Из 9 сотен вычесть 2 сотни получится 7 сотен.
840 − 60 = 84 дес. − 6 дес. − 78 дес. = 780.
Из 84 десятков вычесть 6 десятков получится 78 десятков.
Оформляем задание в тетрадь.
400 + 300 = 700, так как 4 сот. + 3 сот. = 7 сот.
900 − 200 = 700, так как 9 сот. − 2 сот. = 7 сот.
840 − 60 = 780, так как 84 дес. − 6 дес. − 78 дес.
Задание на полях страницы
Набери множителями:

4 ∙ 3 ∙ 6 12 ∙ 3 ∙ 2 4 ∙ 2 ∙ 9
Подбери такие комбинации чисел, чтобы при умножении получалось 72. Для этого перебирай разные числа, чтобы найти верное решение, которых существует множество.
Устные рассуждения.
Умножая данные числа из каждой строки нужно набрать число 72.
Множители можно менять местами.
Вычисляем.
9 ∙ 4 ∙ 2 = 9 ∙ (4 ∙ 2) = 9 ∙ 8 = 72
3 ∙ 4 ∙ 6 = 72
1) 3 ∙ 4 = 12
2) 12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72
12 ∙ 3 ∙ 2 = 12 ∙ (3 ∙ 2) = 12 ∙ 6 = 72
Записываем решение в тетрадь.
9 ∙ 4 ∙ 2 = 72
3 ∙ 4 ∙ 6 = 72
12 ∙ 3 ∙ 2 = 72
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Премиум подписка в подарок!
Специально для новых пользователей дарим премиум подписку на 7 дней в подарок, чтобы вы смогли оценить все преимущества приложения.
Получить подпискуПосле нажатия на кнопку "Получить подписку", премиум подписка начнёт действовать ровно 7 дней а затем автоматически отключится.
+





Напишите свой комментарий.