Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 60

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 18.
На складе ☐ велосипедов. Среди них женских велосипедов ☐, мужских – в 3 раза больше, а остальные велосипеды детские. Сколько детских велосипедов на складе?
Дополни условие и реши задачу.
На складе 100 велосипедов. Среди них женских – 20, мужских – в 3 раза больше. Сколько детских велосипедов на складе?

1) 20 · 3 = 60 (шт.) – мужских велосипедов на складе.
2) 60 + 20 = 80 (шт.) – велосипедов женских и мужских на складе всего.
3) 100 – 80 = 20 (шт.) – детских велосипедов на складе.
Ответ: 20 детских велосипедов на складе.
«в 3 раза больше», значит, 3 раза по столько, т.е. умножить на 3.
Дополним условия задачи.
Ты можешь подставить свои числа или воспользоваться нашими.
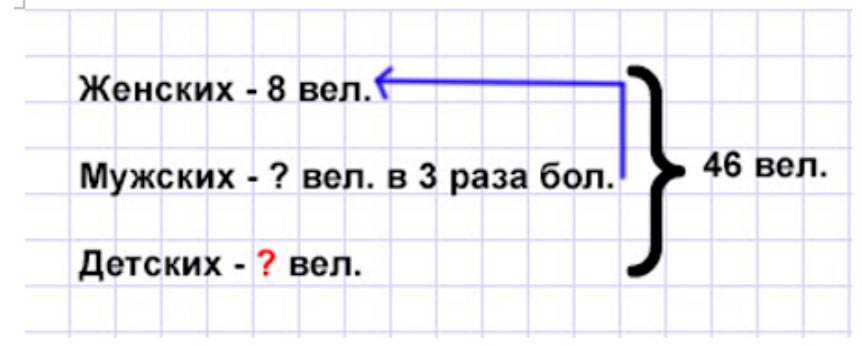
Задача: На складе 46 велосипедов. Среди них женских велосипедов 8, мужских – в 3 раза больше, а остальные велосипеды детские. Сколько детских велосипедов на складе?
Оформляем условие в виде краткой записи.
Рассуждаем.
Мужских велосипедов в 3 раза больше, чем женских.
Это значит, чтобы найти сколько мужских велосипедов, нужно количество женских велосипедов сложить 3 раза. Но сложение одинаковых слагаемых можно заменить умножением.
8 ∙ 3 = 24 (вел.) – мужских.
Продолжаем рассуждение.
Узнаем общее количество женских и мужских велосипедов, для этого сложим их.
24 + 8 = 32 (вел.) – мужских и женских вместе.
Продолжаем рассуждение.
Общее количество велосипедов складывается из женских, мужских и детских.
Чтобы узнать количество детских велосипедов нужно из общего количества велосипедов вычесть сумму мужских и женских велосипедов.
46 – 32 = 14 (вел) – детских.
Записываем ответ.
Ответ: 14 велосипедов.
Решение выражением:
46 – (24 + 8 ∙ 3) = 14 (вел.) – детских,
где 8 ∙ 3 – количество мужских велосипедов.
Номер 19.
Расфасовали 16 кг крупы поровну в 8 пакетов. Сколько пакетов потребуется, чтобы расфасовать 90 кг крупы, если в каждом пакете крупы будет на 1 кг больше, чем было?
Ответ:
1) 16 : 8 = 2 (кг) – крупы в одном пакете. 2) 2 + 1 = 3 (кг) – крупы в пакете станет. 3) 90 : 3 = 30 (п.) – понадобится. Ответ: 30 пакетов потребуется, чтобы расфасовать 90 кг крупы.
Данная задача: вида «Масса 1 предмета, количество предметов, общая масса» характеризуется зависимостями между элементами:
Масса 1 пакета · количество пакетов = общая масса.
Общая масса : масса 1 пакета = количество пакетов.
Общая масса : количество пакетов = масса 1 пакета.
Оформляем условие в виде таблицы.

Рассуждаем.
Масса 8 пакетов равна 16 кг. Пакеты одинаковые, т.е. масса крупы в них одинаковая.
Чтобы узнать, какова масса одного пакета, нужно общую массу пакетов разделить на количество пакетов.
16 : 8 = 2 (кг) — масса одного пакета.
Продолжаем рассуждение.
Теперь в каждом пакете на 1 кг крупы больше, это столько же, но ещё плюс 1 кг.
2 + 1 = 3 (кг) — крупы станет в одном новом пакете.
Продолжаем рассуждение.
Масса одного пакета 3 кг. А сколько пакетов нужно для 90 кг крупы неизвестно.
Чтобы узнать количество пакетов, нужно общую массу крупы разделить на массу 1 пакета.
90 : 3 = 9 дес. : 3 = 3 дес. = 30 (п.) — потребуется для 90 кг крупы.
Записываем ответ.
Ответ: 30 пакетов.
Номер 20.
Из 10 кг сахарной свеклы получают 2 кг сахару. Сколько килограммов сахару можно получить из 40 кг свеклы? из 80 кг? из 100 кг?
Ответ:
1) 10 : 2 = 5 (кг) – свеклы нужно для изготовления 1 кг сахара. 2) 40 : 5 = 8 (кг) – сахару можно получить. 3) 80 : 5 = 16 (кг) – сахару можно получить. 4) 100 : 5 = 20 (кг) – сахару можно получить. Ответ: 8 кг сахару можно получить из 40 кг свёклы, 16 кг сахару можно получить из 80 кг свёклы, 20 кг сахару можно получить из 100 кг свёклы.
Данная задача: вида «Масса свеклы, масса сахара, масса свеклы на 1 кг сахара» характеризуется зависимостями между элементами:
Масса свеклы на 1 кг сахара · масса сахара = масса свеклы.
Масса свеклы : масса свеклы на 1 кг сахара = масса сахара.
Масса свеклы : масса сахара = масса свеклы на 1 кг сахара.
Оформляем условие в виде таблицы.
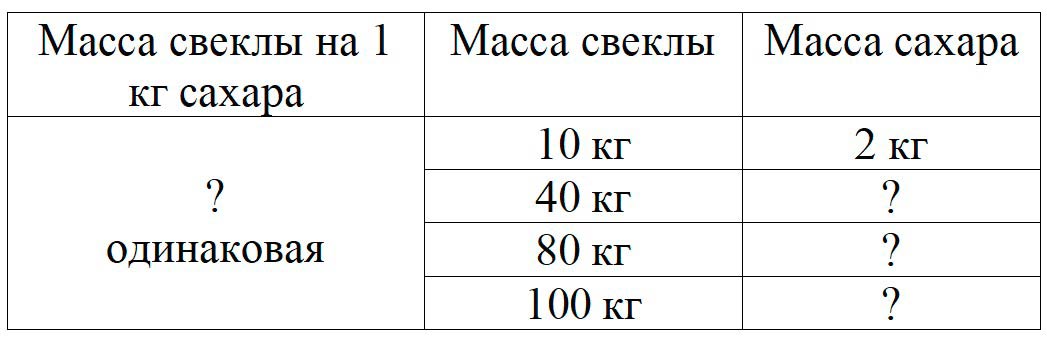
Рассуждаем.
Для 2 кг сахара требуется 10 кг свеклы. Чтобы узнать сколько потребуется свеклы на 1 кг сахара нужно массу свеклы разделить на массу сахара.
10 : 2 = 5 (кг) – свеклы потребуется на 1 кг сахара.
Продолжаем рассуждение.
Мы узнали, что на 1 кг сахара потребуется 5 кг свеклы.
Значит, чтобы узнать сколько получится сахара из определенной массы свеклы нужно массу свеклы разделить на массу свеклы на 1 кг сахара.
40 : 5 = 8 (кг) – сахара можно получить из 40 кг свеклы;
80 : 5 = (50 + 30) : 5 = 10 + 6 = 16 (кг) – сахара можно получить из 80 кг свеклы;
100 : 5 = 10 дес. : 5 = 2 дес. = 20 (кг) – сахара можно получить из 100 кг свеклы.
Записываем ответ.
Ответ: из 40 кг свеклы – 8 кг сахара; из 80 кг свеклы – 16 кг сахара; из 100 кг свеклы – 20 кг сахара.
Номер 21.
Вычисли значения выражений а + b и b − а, если а = 23, b = 100; а = 100, b = 450.
Ответ:
Чтобы найти значение буквенного выражения нужно вместо неизвестной буквы подставить данное число и вычислить.
Рассуждаем.
а + b – это значит, что значение а нужно увеличить на b;
b − а – значит, что из значения b нужно вычесть значение b.
Вычисляем.
а + b, если:
а = 23, b = 100, то 23 + 100 = 123
а = 100, b = 450, то 100 + 450 = 550
b − а, если:
а = 23, b = 100, то 100 − 23 = 77
а = 100, b = 450, то 450 − 100 = 350
Оформляем задание в тетрадь.
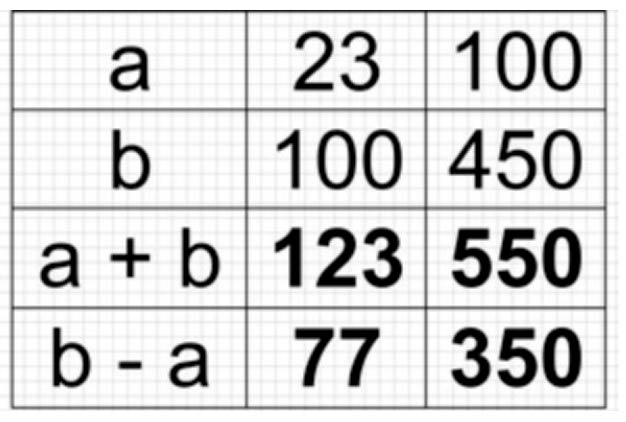
Номер 22.
Ответ:

а ∙ b, значит значение а нужно умножить на b.
с : k, значит, значение с нужно разделить на k.
Рассуждаем.
26 ∙ 3 = (20 + 6) ∙ 3 = 60 + 18 = 78
? ∙ 4 = 96
Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
96 : 4 = (80 + 16) : 4 = 20 + 4 = 24
9 ∙ ? = 63
Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
63 : 9 = 7
82 ∙ ? = 82
Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
82 : 82 = 1
Оформляем задание в тетрадь.
.jpg)
Рассуждаем.
72 : 4 = (40 + 32) : 4 = 10 + 8 = 18
60 : ? = 6
Чтобы найти делитель нужно делимое разделить на частное.
60 : 6 = 10
37 : ? = 37
Чтобы найти делитель нужно делимое разделить на частное.
37 : 37 = 1
? : 2 = 44
Чтобы найти делимое нужно частное умножить на делитель.
44 ∙ 2 = 88
Оформляем задание в тетрадь.
.jpg)
Номер 23.
В большой бидон помещается 15 л молока, а в банку – пятая часть молока из бидона. Сколько литров молока входит в одну банку? Сколько нужно банок, чтобы разлить в них молоко из трех полных бидонов?
Ответ:
1) 15 : 5 = 3 (л) – в 1 банке. 2) 15 ∙ 3 = 45 (л) – в 3 бидонах. 3) 45 : 3 = 15 (б.) – понадобится. Ответ: 3 л молока входит в одну банку, 15 банок нужно для того, чтобы разлить молоко из 3 полных бидонов.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде краткой записи.

Рассуждаем.
В одной банке пятая часть от бидона, значит емкость бидона нужно разделить на 5 одинаковых частей и взять одну такую часть.
15 : 5 = 3 (л) – вместимость 1 банки.
Продолжаем рассуждение.
Чтобы узнать сколько литров в трех бидонах нужно вместимость одного бидона умножить на 3.
15 ∙ 3 = (10 + 5) ∙ 3 = 30 + 15 = 45 (л) – в 3 бидонах.
Продолжаем рассуждение.
Чтобы узнать сколько потребуется банок для 45 литра молока нужно общий объем молока разделить на вместимость одной банки.
45 : 3 = 15 (б.) – нужно для 45 л.
Записываем ответ.
Ответ: 15 банок.
Номер 24.
На сколько минут дольше шел спектакль, чем кинофильм, если спектакль продолжался 80 мин, а кинофильм 1 ч 10 мин?
Ответ:
1) 1 ч 10 мин = 60 + 10 = 70 (мин) - длится кинофильм 2) 80 − 70 = 10 (мин) – на столько дольше длился спектакль, чем кинофильм. Ответ: на 10 мин дольше шёл спектакль, чем кинофильм.
1) Помни, что 1 ч = 60 мин.
2) Вспомни, что сравнивать время можно только, выраженные в одних единицах времени, например в минутах.
Оформляем условие в виде краткой записи.
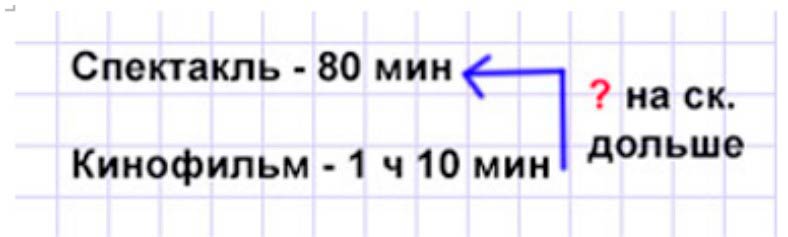
Рассуждаем.
Переведем время, за которое шёл кинофильм в минуты.
1 ч 10 мин = 60 мин + 10 мин = 70 мин.
Продолжаем рассуждение.
Чтобы узнать на сколько дольше шёл спектакль, чем кинофильм нужно из большего времени вычесть меньшее.
80 − 70 = 10 (мин) – на сколько дольше шёл спектакль, чем кинофильм.
Записываем ответ.
Ответ: на 10 минут.
Номер 25.
Ответ:46 : 6 = 7 (ост. 4) 65 : 7 = 9 (ост. 2) 39 : 4 = 9 (ост. 3) 54 : 8 = 6 (ост. 6)
1) Повтори деление с остатком;
2) Помни, что остаток всегда должен быть меньше делителя.
Рассуждаем.
? : 6 = 7 (ост. 4)
Чтобы найти делимое, нужно делитель умножить на частное и к произведению прибавить остаток.
1) Найдем неполное делимое: 6 ∙ 7 = 42
2) Найдем делимое: 42 + 4 = 46
Значит, 46 : 6 = 7 (ост. 4)
? : 4 = 9 (ост. 3)
Чтобы найти делимое, нужно делитель умножить на частное и к произведению прибавить остаток.
1) Найдем неполное делимое: 9 ∙ 4 = 36
2) Найдем делимое: 36 + 3 = 39
Значит, 39 : 4 = 9 (ост. 3)
65 : ? = 9 (ост. 2)
Чтобы найти делитель нужно неполное делимое разделить на частное.
1) Найдем неполное делимое: 65 – 2 = 63
2) Найдем делитель: 63 : 9 = 7
Значит, 65 : 7 = 9 (ост. 2)
54 : ? = 6 (ост. 6)
Чтобы найти делитель нужно неполное делимое разделить на частное.
1) Найдем неполное делимое: 54 – 6 = 48
2) Найдем делитель: 48 : 6 = 8
Значит, 54 : 8 = 6 (ост. 6)
Сделаем проверку.
Чтобы сделать проверку нужно:
1) убедиться, что остаток меньше делителя;
2) частное умножить на делитель и прибавить к произведению остаток, должно получиться делимое.
Если хотя бы один пункт не выполняется, то деление выполнено не верно.
46 : 6 = 7 (ост. 4)
Проверка:
1) 6 ∙ 7 = 42 – неполное делимое
2) 42 + 4 = 46 – делимое
46 = 46
3) 4 < 6 – остаток должен быть меньше делителя.
39 : 4 = 9 (ост. 3)
Проверка:
1) 9 ∙ 4 = 36 – неполное делимое
2) 36 + 3 = 39 – делимое
39 = 39
3) 3 < 4 – остаток должен быть меньше делителя.
65 : 7 = 9 (ост. 2)
Проверка:
1) 9 ∙ 7 = 63 – неполное делимое
2) 63 + 2 = 65 – делимое
65 = 65
3) 2 < 7 – остаток должен быть меньше делителя.
54 : 8 = 6 (ост. 6)
Проверка:
1) 6 ∙ 8 = 48 – неполное делимое
2) 48 + 6 = 54 – делимое
54 = 54
3) 6 < 8 – остаток должен быть меньше делителя.
Оформим задание в тетрадь.
46 : 6 = 7 (ост. 4)
6 ∙ 7 + 4 = 42 + 4 = 46 – делимое.
39 : 4 = 9 (ост. 3)
9 ∙ 4 + 3 = 36 + 3 = 39 – делимое.
65 : 7 = 9 (ост. 2)
(65 – 2) : 9 = 63 : 9 = 7 – делитель.
54 : 8 = 6 (ост. 6)
(54 – 6) : 6 = 48 : 6 = 8 – делитель.
Номер 26.
Ответ:

1) Вспомни как найти деление методом подбора;
2) Помни о порядке выполнения арифметических действий.
Расставляем порядок действий и выполняем вычисления.
Выполним деление методом подбора:
92 : 23 = 4
Пробуем в частном 2 и проверяем: 23 ∙ 2 = 46, 46 < 92, число 2 не подходит.
Пробуем в частном 3 и проверяем: 23 ∙ 3 = 69, 69 < 92, число 3 не подходит.
Пробуем в частном 4 и проверяем: 23 ∙ 3 = 92, 92 = 92, значит 92 : 23 = 4.
Ответ: 4.
68 : 17 = 4
Пробуем в частном 2 и проверяем: 17 ∙ 2 = 34, 34 < 68, число 2 не подходит.
Пробуем в частном 3 и проверяем: 17 ∙ 3 = 51, 51 < 68, число 3 не подходит.
Пробуем в частном 4 и проверяем: 17 ∙ 4 = 68, 68 = 68, значит 68 : 17 = 4.
Ответ: 4.
57 : 19 = 3
Пробуем в частном 2 и проверяем: 19 ∙ 2 = 38, 38 < 57, число 2 не подходит.
Пробуем в частном 3 и проверяем: 19 ∙ 3 = 57, 57 = 57, значит 57 : 19 = 3.
Ответ: 3.
52 : 26 = 2
Пробуем в частном 2 и проверяем: 26 ∙ 2 = 52, 52 = 52, значит 52 : 26 = 2.
Ответ: 2.
96 : 24 = 4
Пробуем в частном 2 и проверяем: 24 ∙ 2 = 48, 48 < 96, число 2 не подходит.
Пробуем в частном 3 и проверяем: 24 ∙ 3 = 72, 72 < 96, число 3 не подходит.
Пробуем в частном 4 и проверяем: 24 ∙ 4 = 96, 96 = 96, значит 96 : 24 = 4.
Ответ: 4.
68 : 34 = 2
Пробуем в частном 2 и проверяем: 34 ∙ 2 = 68, 68 = 68, значит 68 : 34 = 2.
Ответ: 2.
64 : 16 = 4
Пробуем в частном 2 и проверяем: 16 ∙ 2 = 32, 32 < 64, число 2 не подходит.
Пробуем в частном 3 и проверяем: 16 ∙ 3 = 48, 48 < 64, число 3 не подходит.
Пробуем в частном 4 и проверяем: 16 ∙ 4 = 64, 64 = 64, значит 64 : 16 = 4.
Ответ: 4.
44 : 11 = 4
Пробуем в частном 2 и проверяем: 11 ∙ 2 = 22, 22 < 44, число 2 не подходит.
Пробуем в частном 3 и проверяем: 11 ∙ 3 = 33, 33 < 44, число 3 не подходит.
Пробуем в частном 4 и проверяем: 11 ∙ 4 = 44, 44 = 44, значит 44 : 11 = 4.
Ответ: 4.
Выполним вычисления по действиям:
66 : 33 + 99 : 9 = 13
1) 66 : 33 = 2
2) 99 : 9 = 11
3) 2 + 11 = 13
88 : 22 + 15 ∙ 6 = 94
1) 88 : 22 = 4
2) 15 ∙ 6 = (10 + 5) ∙ 6 = 60 + 30 = 90
3) 4 + 90 = 94
65 : (213 − 200) ∙ 10 = 50
1) 213 − 200 = 200 + 13 − 200 = 13
2) 65 : 13 = 5
3) 5 ∙ 10 = 50
84 : 12 ∙ (307 − 300) = 49
1) 307 − 300 = 300 + 7 − 300 = 7
2) 84 : 12 = 7
2) 7 ∙ 7
Оформляем задание в тетрадь.
92 : 23 = 4, так как 23 ∙ 4 = 92
68 : 17 = 4, так как 17 ∙ 4 = 68
57 : 19 = 3, так как 19 ∙ 3 = 57
52 : 26 = 2, так как 26 ∙ 2 = 52
96 : 24 = 4, так как 24 ∙ 4 = 96
68 : 34 = 2, так как 34 ∙ 2 = 68
64 : 16 = 4, так как 16 ∙ 4 = 64
44 : 11 = 4, так как 11 ∙ 4 = 44
66 : 33 + 99 : 9 = 2 + 11 = 13
88 : 22 + 15 ∙ 6 = 4 + 90 = 94
65 : (213 − 200) ∙ 10 = 65 : 13 ∙ 10 = 5 ∙ 10 = 50
84 : 12 ∙ (307 − 300) = 84 : 12 ∙ 7 = 7 ∙ 7 = 49
Задание на полях страницы
Занимательные рамки:


Первая рамка:
34 + 10 + 56 = 90 + 10 = 100
56 + 17 + 27 = 56 + 44 = 100
34 + 39 + 27 = 34 + 66 = 100
Вторая рамка:
48 + 34 + 13 = 48 + 47 = 95
13 + 67 + 15 = 80 + 15 = 95
48 + 32 + 15 = 80 + 15 = 95
Занимательные рамки – рамки, в которых числа, стоящие на одной прямой, образуют в сумме число, записанное в центре рамки.
Рассуждаем.
Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки – это число 100.
Находим неизвестные числа.
34 + 10 + 56 = 100
56 + 17 + 27 = 100
34 + 39 + 27 = 100
Заполняем рамку числами.
.jpg)
Рассуждаем.
Нужно подобрать такое число, чтобы сумма двух крайних чисел и неизвестного числа между ними равнялась числу в середине рамки – это число 95.
Находим неизвестные числа.
48 + 34 + 13 = 95
48 + 32 + 15 = 95
13 + 67 + 15 = 95
Заполняем рамку числами.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.