Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 47

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Увеличь в 10 раз числа: 8, 12, 35. Уменьши в 100 раз числа: 700, 400, 100. Уменьши в 10 раз числа: 840, 900, 360.
Ответ:80, 120, 350. 7, 4, 1. 84, 90, 36.
Повтори как можно получить число, которое больше или меньше данного в 10 раз; в 100 раз.
Как можно получить число, которое больше или меньше данного в 10 раз; в 100 раз.
Повтори, как можно получить число, которое больше или меньше данного в 10 раз; 100 раз.
Рассуждаем.
Увеличить число в 10 раз, это значит данное число нужно умножить на 10.
Чтобы умножить число на 10, нужно к нему справа приписать один нуль.
8 ∙ 10 = 80
12 ∙ 10 = 120
35 ∙ 10 = 350
Продолжаем рассуждение.
Уменьшить число в 100 раз, значит число нужно разделить на 100.
Чтобы разделить число на 100, нужно убрать у него справа два нуля.
700 : 100 = 7
400 : 100 = 4
100 : 100 = 1
Продолжаем рассуждение.
Уменьшить число в 10 раз, значит число нужно разделить на 10.
Чтобы разделить число на 10, нужно убрать у него справа один нуль.
700 : 10 = 70
400 : 10 = 40
100 : 10 = 10
Оформляем задание в тетрадь.
Увеличь в 10 раз числа:
8 ∙ 10 = 80
12 ∙ 10 = 120
35 ∙ 10 = 350
Уменьши в 100 раз числа:
700 : 100 = 7
400 : 100 = 4
100 : 100 = 1
Уменьши в 10 раз числа:
700 : 10 = 70
400 : 10 = 40
100 : 10 = 10
Номер 2.
На каждом этаже девятиэтажного дома по три квартиры. Номера квартир на седьмом этаже: 127, 128, 129. Назови номера трех квартир на следующем этаже; на предыдущем этаже.
Ответ:На следующем этаже: 130, 131, 132. На предыдущем этаже: 124, 125, 126.
1) Вспомни, как получается каждое следующее число при счете.
2) Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Последняя квартира на 7 этаже имеет № 129.
Значит, чтобы узнать номер следующей квартиры, нужно к числу 129 прибавить 1. На 8 этаже таких квартир три.
129 + 1 = 130
130 + 1 = 131
131 + 1 = 132
Продолжаем рассуждение.
Первая квартира на 7 этаже имеет №127.
Значит, чтобы узнать номер предыдущей квартиры, нужно из числа 127 вычесть 1. На 6 этаже также три квартиры.
127 – 1 = 126
126 – 1 = 125
125 – 1 = 124
Оформляем задание в тетрадь.
На следующем этаже: 130, 131, 132.
На предыдущем этаже: 124, 125, 126.
Номер 3.
В лыжной эстафете участвовали 9 команд мальчиков, по 8 человек в каждой, и еще 24 девочки. Во сколько раз больше мальчиков, чем девочек, участвовало в эстафете?
Измени вопрос, чтобы последним действием при решении было вычитание. Реши новую задачу.

Задача 1:
1) 8 · 9 = 72 (м.) – участвовало
2) 72 : 24 = 3 (раза) – больше мальчиков, чем девочек
Ответ: в 3 раза больше мальчиков, чем девочек участвовало в эстафете.
Задача 2:
1) 8 · 9 = 72 (м.) – участвовало
2) 72 - 24 = 48 (чел.) – больше мальчиков
Ответ: в эстафете участвовало на 48 человек больше мальчиков, чем девочек.
1) «Во сколько раз больше» – вычисляется делением;
2) «Во сколько раз меньше» – вычисляется вычитанием.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
9 команд по 8 человек, это значит, что в каждой команде 8 человек и таких команд 9. Сложение одинаковых слагаемых, можно заменить умножением.
9 ∙ 8 = 72 (чел.) – мальчиков.
Продолжаем рассуждение.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
2) 72 : 24 = 3 (раз) – во столько раз больше мальчиков, чем девочек.
Записываем ответ.
Ответ: в 3 раза.
На сколько мальчиков участвовало в эстафете больше, чем девочек.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
В предыдущей задаче мы уже узнали, что мальчиков в эстафете участвовало 72.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее.
72 – 24 = 48 (чел.) – на сколько больше мальчиков, чем девочек.
Записываем ответ.
Ответ: на 48 человек.
Номер 4.
Ответ:1 м = 10 дм, потому что 10 дм = 10 дм 1 м > 10 см, потому что 100 см > 10 см 1 дм2 > 10 см2, потому что 100 см2>10 см2 1 дм = 10 см, потому что 10 см = 10 см 1 дм > 10 мм, потому что 100 мм > 10 мм 1 см2 = 100 мм2, потому что 100 мм2 = 100 мм2
1) Помни, что
1 м = 10 дм = 100 см;
1 см2 = 100 мм2;
1 дм2 = 100 см2.
2) Помни, что сравнивать числовые значения длины можно только если они выражены в одних единицах измерения.
Рассуждаем.
Сравним 1 м и 10 дм.
Переведем 1 м в дециметры:
1 м = 10 дм
10 дм = 10 дм, значит 1 м = 10 дм.
Ставим знак равно.
Сравним 1 м и 10 см
Переведем 1 м в сантиметры:
1 м = 100 см
100 см > 10 см, значит 1 м > 10 см.
Ставим знак больше.
Сравним 1 дм2 и 10 см2.
Переведем 1 дм2 в сантиметры квадратные:
1 дм2 = 10 см ∙ 10 см = 100 см2
100 см2 > 10 см2, значит 1 дм2 > 10 см2
Ставим знак больше.
Сравним 10 дм и 10 см
Переведем 10 дм в сантиметры:
10 дм = 10 ∙ 10 см = 100 см
100 см > 10 см, значит 10 дм > 10 см.
Ставим знак больше.
Сравним 1 дм и 10 мм
Переведем 1 дм в миллиметры:
1 дм = 10 см = 100 мм
100 мм > 10 мм, значит 1 дм > 10 мм.
Ставим знак больше.
Сравним 1 см2 и 100 мм2.
Переведем 1 см2 в миллиметры квадратные:
1 см2 = 10 мм ∙ 10 мм = 100 мм2
100 мм2 = 100 мм2, значит 1 см2 = 100 мм2.
Ставим знак равно.
Оформляем задание в тетрадью
1 м = 10 дм, так как 10 дм = 10 дм
1 м > 10 см, так как 100 см > 10 см
1 дм2 > 10 см2, так как 100 см2 > 10 см2
10 дм > 10 см, так как 100 см > 10 см
1 дм > 10 мм, так как 100 мм > 10 мм
1 см2 = 100 мм2, так как 100 мм2 = 100 мм2
Номер 5.
Реши уравнения и сделай проверку.
Ответ:х : 3 = 17
х = 17 · 3
х = 51
Проверка:
51 : 3 = 17
17 = 17
Ответ: 51
49 – х = 28
х = 49 – 28
х = 21
Проверка:
49 – 21 = 28
28 = 28
Ответ: 21
64 : х = 4
х = 64 : 4
х = 16
Проверка:
64 : 16 = 4
4 = 4
Ответ: 16
Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассмотрим уравнения.
х : 3 = 17
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
49 – х = 28
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность.
64 : х = 4
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно значение делимого разделить на значение частного.
Решим уравнение.
х : 3 = 17
х = 17 ∙ 3
х = 51
Ответ: 51.
49 – х = 28
х = 49 − 28
х = 21
Ответ: 21.
64 : х = 4
х = 64 : 4
х = 16
Ответ: 16.
Сделаем проверку.
В уравнение вместо неизвестного подставим найденное значение.
х : 3 = 17
Проверка: вместо неизвестного подставим число 51
51 : 3 = (30 + 21) : 3 = 10 + 7 = 17
17 = 17
Уравнение решено верно.
49 – х = 28
Проверка: вместо неизвестного подставим число 21.
49 – 21 = 28
28 = 28
Уравнение решено верно.
64 : х = 4
Проверка: вместо неизвестного подставим число 16.
64 : 16 = 4
4 = 4
Уравнение решено верно.
Оформляем задание в тетрадь.
х : 3 = 17
х = 17 ∙ 3
х = 51
Проверка:
51 : 3 = 17
17 = 17
49 – х = 28
х = 49 − 28
х = 21
Проверка:
49 – 21 = 28
28 = 28
64 : х = 4
х = 64 : 4
х = 16
Проверка:
64 : 16 = 4
4 = 4
Номер 6.
Ответ:
1) Вспомни, как выполнить деление с остатком.
2) Помни о порядке выполнения арифметических действий.
3) Сначала выполняются действия умножение или деление, а потом – сложение или вычитание. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним вычисления по действиям:
28 + 42 : 7 − 6 = 28
1) 42 : 7 = 6
2) 28 + 6 = 34
3) 34 − 6 = 28
96 − 72 : 9 + 15 = 103
1) 72 : 9 = 8
2) 96 − 8 = 88
3) 88 + 15 = 103
32 + 56 : 8 − 7 = 32
1) 56 : 8 = 7
2) 32 + 7 = 39
3) 39 − 7 = 32
100 − 7 ∙ 8 = 44
1) 7 ∙ 8 = 56
2) 100 − 56 = 44
90 − 8 ∙ 8 = 26
1) 8 ∙ 8 = 64
2) 90 − 64 = 26
80 − 9 ∙ 8 = 8
1) 9 ∙ 8 = 72
2) 80 − 72 = 8
Выполним деление с остатком:
74 : 9 = ?
74 не делится на 9 без остатка. Вспомним, какое самое большое число до 74 делится на 9 без остатка. Это 72.
Найдём частное: 72 : 9 = 8.
Найдём остаток: 74 − 72 = 2.
Значит, 74 : 9 = 8 (ост. 2)
65 : 9 = ?
65 не делится на 9 без остатка. Вспомним, какое самое большое число до 65 делится на 9 без остатка. Это 63.
Найдём частное: 63 : 9 = 7.
Найдём остаток: 65 − 63 = 2.
Значит, 65 : 9 = 7 (ост. 2)
85 : 9 = ?
85 не делится на 9 без остатка. Вспомним, какое самое большое число до 85 делится на 9 без остатка. Это 81.
Найдём частное: 81 : 9 = 9.
Найдём остаток: 85 − 81 = 4.
Значит, 85 : 9 = 9 (ост. 4)
Оформляем задание в тетрадь.
28 + 42 : 7 − 6 = 28 + 6 − 6 = 28 + 0 = 28
96 − 72 : 9 + 15 = 96 − 8 + 15 = 88 + 15 = 103
32 + 56 : 8 − 7 = 32 + 7 − 7 = 32
100 − 7 ∙ 8 = 100 − 56 = 44
90 − 8 ∙ 8 = 90 − 64 = 26
80 − 9 ∙ 8 = 80 − 72 = 8
74 : 9 = 8 (ост. 2)
65 : 9 = 7 (ост. 2)
85 : 9 = 9 (ост. 4)
Номер 7.
1) Рассмотри, как составлены ряды из фигур. 2) Составь все возможные трехзначные числа, используя цифры 2, 7, 5 и не повторяя одну и ту же цифру в записи одного числа.

Ряды из фигур составлены так, что местами меняют фигуры. Сначала на первое место ставят на двух картинках красный круг, а за тем переставляют квадрат и треугольник. На 3 и 4 рисунках на первом месте стоит синий треугольник, а квадрат и круг меняются местами. Аналогично на 5 и 6 картинках, зелёный квадрат на первом месте, а круг и треугольник меняются местами. Фигуры не повторяются и меняются местами. 2) 2, 7, 5 275, 257 725, 752 572, 527
Вспомни как образуются и называются трёхзначные числа.
Рассуждаем.
Рассмотрим ряды фигур.
Ряды фигур составлены так, что фигуры меняют местами без повторений.
Рассмотрим 1 и 2 ряд.
Сначала на первое место ставят красный круг, а квадрат и треугольник меняют местами.
Рассмотрим 3 и 4 ряды.
На первое место теперь ставят треугольник, а квадрат и круг меняют местами.
Рассмотрим 5 и 6 ряды.
На первое место ставят квадрат, а круг и треугольник меняют местами.
Продолжаем рассуждение.
С помощью фигур показано, как можно перебрать все подобные варианты без повторения.
Условно теперь вместо круга подставим число 2, вместо треугольника – число 5, а вместе квадрата – 7.
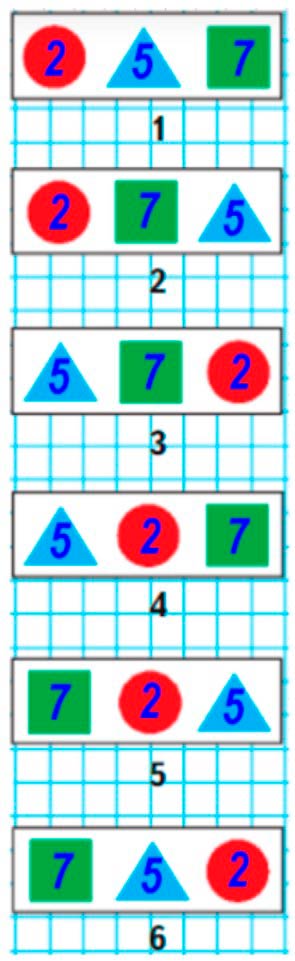
257, 275, 572, 527, 725, 752.
Задание внизу страницы
Уменьши в 100 раз числа: 600, 200, 800.
Ответ:6, 2, 8.
Повтори, как можно получить число, которое больше или меньше данного в 100 раз.
Рассуждаем.
Уменьшить число в 100 раз, значит число нужно разделить на 100.
Чтобы разделить число на 100, нужно убрать у него справа два нуля.
Оформляем задание в тетрадь.
600 : 100 = 6
200 : 100 = 2
800 : 100 = 8
Номер 1.
Ответ:300 + 60 + 3 = 363 509 – 500 = 9
296 – 90 – 6 = 200 900 + 20 = 920
704 + 80 = 784 860 + 7 = 867
654 – 54 = 600 435 – 30 = 405
1) Вспомни как образуются и называются трёхзначные числа.
2) Повтори как разложить число на разрядные слагаемые.
Рассуждаем
300 + 60 + 3 = 3 сот. + 6 дес. + 3 ед. = 363
296 – 90 – 6 = 2 сот. + 9 дес. + 6 ед. – 9 дес. – 6 ед. = 2 сот. = 200
509 – 500 = 5 сот. + 9 ед. – 5 сот. = 9
900 + 20 = 9 сот. + 2 дес. = 920
704 + 80 = 7 сот. + 8 дес. + 4 ед. = 784
654 – 54 = 6 сот. + 5 дес. 4 ед. – 5 дес. 4 ед. = 6 сот. = 600
860 + 7 = 8 сот. + 6 дес. + 7 ед. = 867
435 – 30 = 4 сот. + 3 дес. + 5 ед. – 3 дес. = 4 сот. + 5 ед. = 405
Оформляем задание в тетрадь.
300 + 60 + 3 = 363
296 – 90 – 6 = 200
509 – 500 = 500 + 9 – 500 = 9
900 + 20 = 920
704 + 80 = 700 + 80 + 4 = 784
654 – 54 = 600 + 50 + 4 – 50 – 4 = 600
860 + 7 = 800 + 60 + 7 = 867
435 – 30 = 400 + 30 + 5 – 30 = 405
Номер 2.
Ответ:

1) a + 1, значит, к значению a нужно прибавить 1, т.е. увеличить на 1.
2) с – 1, значит, из значения с нужно вычесть 1, т.е. уменьшить на 1.
Вычислим 1 таблицу.
Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число и вычислить.
а + 1, если:
а = 9, то 9 + 1 = 10
а = 99, то 99 + 1 = 100
а = 999, то 999 + 1 = 1000
Вычислим 2 таблицу.
Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число и вычислить.
с – 1, если:
с = 10, то 10 – 1 = 9
с = 100, то 100 – 1 = 99
с = 1000, то 1000 – 1 = 999
Оформляем задание в тетрадь.
.jpg)
Номер 3.
Ответ:905 = 900 + 5 820 = 800 + 20 199 = 100 + 90 + 9
1) Вспомни, как образуются и называются трёхзначные числа.
2) Повтори, как разложить число на разрядные слагаемые.
Рассуждаем.
905 – число состоит из 9 сот. и 5 ед.
905 = 9 сот. + 0 дес. + 5 ед. = 900 + 5
Разряд десятков отсутствует.
820 – число состоит из 8 сот. и 2 дес.
820 = 8 сот. + 2 дес. + 0 ед. = 800 + 20
Разряд единиц отсутствует.
199 – число состоит из 1 сот., 9 дес. и 9 ед.
199 = 1 сот + 9 дес. + 9 ед. = 100 + 90 + 9
Все разряды присутствуют.
Оформляем задание в тетрадь.
905 = 900 + 5
820 = 800 + 20
199 = 100 + 90 + 9
Номер 4.
Чему равна площадь квадрата со стороной 9 дм? 9 см? 9 м?
Ответ:
1) 9 ∙ 9 = 81 (дм2) – площадь квадрата со стороной 9 дм. 2) 9 ∙ 9 = 81 (см2) – площадь квадрата со стороной 9 см. 3) 9 ∙ 9 = 81 (м2) – площадь квадрата со стороной 9 м. Ответ: площадь квадрата со стороной 9 дм равна 81 дм2; площадь квадрата со стороной 9 см равна 81 см2; площадь квадрата со стороной 9 м равна 81 м2.
Площадь – часть плоскости, которую занимает фигура.
Рассуждаем.
Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
Вычисляем.
1) 9 дм ∙ 9 дм = 81 дм2 – площадь квадрата со стороной 9 дм;
2) 9 см ∙ 9 см = 81 см2 – площадь квадрата со стороной 9 см;
3) 9 м ∙ 9 м = 81 м2 – площадь квадрата со стороной 9 м.
Записываем ответ.
Ответ: 81 дм2; 81 см2; 81 м2.
Номер 5.
Купили 5 ручек по цене ☐ р. и 3 карандаша по цене ☐ р. Сколько стоила эта покупка? Дополни условие и реши задачу.
Ответ:Купили 5 ручек по цене 20 р. и 3 карандаша по цене 10 р. Сколько стоила покупка?

1) 20 · 5 = 100 (р.) – стоило 5 ручек.
2) 10 · 3 = 30 (р.) – стоят карандаши.
3) 100 + 30 = 130 (р.) – стоит покупка.
Ответ: 130 рублей стоила вся покупка всего.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : количество = цена.
Стоимость : цена = количество.
Дополняем условия задачи.
Купили 5 ручек по цене 20 р. и 3 карандаша по цене 10 р. Сколько стоила покупка?
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Общая стоимость ручек складывается из стоимости каждой ручки. Стоимость каждой ручки одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
20 ∙ 5 = 2 дес. ∙ 5 = 10 дес. = 100 (р.) – стоило 5 ручек.
Продолжаем рассуждение.
Общая стоимость карандашей складывается из стоимости каждого карандаша. Стоимость каждого карандаша одинакова. Значит, сложение одинаковых слагаемых можно заменить умножением.
10 ∙ 3 = 30 (р.) – стоят 3 карандаша.
Продолжаем рассуждение.
Общая стоимость складывается из стоимости ручек и карандашей. Чтобы узнать общую стоимость, нужно сложить стоимость всех ручек и карандашей.
100 + 30 = 130 (р.) – стоит вся покупка.
Записываем ответ.
Ответ: 130 рублей.
Номер 6.
От дома до работы маме нужно ехать 20 мин на автобусе и еще 10 мин идти пешком. Сколько времени у нее уходит на дорогу от дома до работы и обратно, если автобус она ждёт 5 мин? Составь задачу, решение которой даст ответ на вопрос: "Сколько времени уходит на дорогу от дома до работы и обратно у твоих мамы или папы?"
Ответ:
1-й способ решения: 1) 20 + 10 + 5 = 35 (мин) – время пути на работу; 2) 35 · 2 = 70 (мин) – время на дорогу туда и обратно. Ответ: 70 минут тратит мама на дорогу от работы и обратно.
Задача:
От дома до работы маме нужно идти до метро 15 минут, в метро ехать 25 минут и путь от метро до работы – 7 минут. Сколько времени у неё уходит на дорогу от дома до работы и обратно?
1) 15 + 25 + 7 = 47 (мин) – общее время в одну сторону;
2) 47 + 47 = 94 (мин) – время на дорогу от дома до работы и обратно.
Ответ: 94 минуты тратит папа на дорогу от работы и обратно.
2-й способ решения: 1) 20 + 20 = 40 (мин) – на автобусе туда и обратно; 2) 10 + 10 = 20 (мин) – пешком туда и обратно; 3) 5 + 5 = 10 (мин) – общее время ожидания автобуса; 4) 40 + 20 + 10 = 70 (мин) – время на дорогу туда и обратно. Ответ: 70 минут тратит мама на дорогу от работы и обратно.
Задача:
От дома до работы маме нужно идти до метро 15 минут, в метро ехать 25 минут и путь от метро до работы – 7 минут. Сколько времени у неё уходит на дорогу от дома до работы и обратно?
1) 15 + 25 + 7 = 47 (мин) – общее время в одну сторону;
2) 47 + 47 = 94 (мин) – время на дорогу от дома до работы и обратно.
Ответ: 94 минуты тратит папа на дорогу от работы и обратно.
Помни, что 1 ч = 60 мин.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Время пути до работы складывается из времени ожидания автобуса, поездке на автобусе и времени, пройденного пешком.
20 + 10 + 5 = 35 (мин.) – время пути до работы.
Продолжаем рассуждение.
Время, потраченное на дорогу до работы и обратно, одинаково. Значит, сложение одинаковых слагаемых можно заменить умножением.
35 ∙ 2 = 70 (мин.) – время на дорогу туда и обратно.
Записываем ответ.
Ответ: 70 минут у мамы уходит на дорогу.
Рассуждаем.
В пути мама была в автобусе 2 раза по 20 минут. Значит, чтобы узнать, сколько времени она провела в автобусе, нужно время умножить на 2.
20 ∙ 2 = 40 (мин) – путь на автобусе туда и обратно.
Продолжаем рассуждение.
В пути мама шла пешком 2 раза по 10 минут. Значит, чтобы узнать, сколько времени она провела в автобусе, нужно время умножить на 2.
10 ∙ 2 = 20 (мин) – путь пешком туда и обратно.
Продолжаем рассуждение.
В пути мама 2 раза ждала автобус по 5 минут. Значит, чтобы узнать, сколько времени она потратила на ожидание, нужно время умножить на 2.
5 ∙ 2 = 10 (мин) – ушло на ожидание автобуса туда и обратно.
Продолжаем рассуждение.
Общее время складывается из времени в автобусе и времени пройденное пешком. Чтобы узнать общее время, нужно сложить эти два времени.
40 + 20 + 10 = 70 (мин) – время на дорогу туда и обратно.
Записываем ответ.
Ответ: 70 минут у мамы уходит на дорогу.
Составляем задачу.
От дома до работы маме нужно идти до метро 15 минут, в метро ехать 25 минут и путь от метро до работы – 7 минут. Сколько времени у неё уходит на дорогу от дома до работы и обратно?
Решаем задачу.
1) 15 + 25 + 7 = 47 (мин) – общее время в одну сторону;
2) 47 + 47 = 94 (мин) – время на дорогу от дома до работы и обратно.
Записываем ответ.
Ответ: 94 минуты тратит мама на дорогу от дома до работы и обратно.
Номер 7.
Ответ:
1) Помни о порядке выполнения арифметических действий, и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Вспомни, как найти деление методом подбора.
Расставляем порядок действий и вычисляем.
79 – 19 ∙ 2 + 34 = 75
1) 19 ∙ 2 = (10 + 9) ∙ 2 = 20 + 18 = 38
2) 79 – 38 = 41
3) 41 + 34 = 75
98 – 20 – 6 ∙ 12 = 6
1) 6 ∙ 12 = 6 ∙ (10 + 2) = 60 + 12 = 72
2) 98 – 20 = 78
3) 78 – 72 = 6
78 : (64 – 58) = 13
1) 64 – 58 = 6
2) 78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
9 ∙ (42 – 37) = 45
1) 42 – 37 = 5
2) 9 ∙ 5 = 45
45 : 15 = ?
Пробуем в частном 3 и проверяем:
15 ∙ 3 = 45,
45 = 45, значит,
45 : 15 = 3.
96 : 24 = ?
Пробуем в частном 4 и проверяем:
24 ∙ 4 = 96,
96 = 96, значит,
96 : 24 = 4.
Оформляем задание в тетрадь.
79 – 19 ∙ 2 + 34 = 79 – 38 + 34 = 41 + 34 = 75
98 – 20 – 6 ∙ 12 = 98 – 20 – 72 = 78 – 72 = 6
78 : (64 – 58) = 78 : 6 = 13
9 ∙ (42 – 37) = 9 ∙ 5 = 45
45 : 15 = 3
96 : 24 = 4
Задание вверху страницы.
Используя рисунок, обьясни записи и выполни вычисления.
Реши с объяснением, используя рисунок.

200 + 10 + 3 = 213 213 = 200 + 10 + 200 + 13 = 210 + 3 203 + 10 213 – 10 213 – 13 213 – 200 213 – 3
Ответ:200 + 10 + 3 = 2 сот. + 1 дес. + 3 ед. = 213 213 = 2 сот. + 1 дес. + 3 ед. = 200 + 10 + 3 200 + 13 = 2 сот. + 1 дес. + 3 ед. = 200 + 10 + 3 = 213 210 + 3 = 2 сот. + 1 дес. + 3 ед. = 200 + 10 + 3 = 213 203 + 10 = 2 сот. + 1 дес. + 3 ед. = 200 + 3 + 10 = 213 213 – 10 = 2 сот. + 1 дес. + 3 ед. – 1 дес. = 2 сот. + 0 дес. + 3 ед. = 203 213 – 13 = 2 сот. + 1 дес. 3 ед. – 1 дес. 3 ед. = 2 сот. = 200 213 – 200 = 2 сот. + 1 дес. 3 ед. – 2 сот. = 13 213 – 3 = 2 сот. + 1 дес. + 3 ед. – 3 ед. = 2 сот. + 1 дес. = 210
1) Вспомни, как образуются и называются трёхзначные числа.
2) Повтори, как разложить число на разрядные слагаемые.
Рассуждаем.
200 + 10 + 3 = 213
К 2 стопкам по 100 палочек прибавили 1 стопку с 10 палочками и потом прибавили ещё 3 палочки, получилось 213 палочек.
213 = 200 + 10 + 3
213 палочек разложили как 2 стопки по 100 палочек, 1 стопку по 10 палочек и 3 палочки.
200 + 13 = 213
К 2 стопкам по 100 палочек прибавили 13 палочек, получили 213 палочек.
210 + 3 = 213
К 2 стопкам по 100 палочек и 1 стопке с 10 палочками прибавили ещё 3 палочки, получилось 213 палочек.
203 + 10 = 213
К 2 стопкам по 100 палочек и 3 палочкам прибавили 1 стопку с 10 палочками, получилось 213.
213 – 10 = 200 + 10 + 3 – 10 = 203
Из 2 стопок по 100 палочек, 1 стопке с 10 палочками и 3 палочек вычли 1 стопку с 10 палочками, получилось 203.
213 – 13 = 200 + 10 + 3 – 13 = 200
Из 2 стопок по 100 палочек, 1 стопке с 10 палочками и 3 палочек вычли 1 стопку с 10 палочками и ещё 3 палочки, получилось 200 палочек.
213 – 200 = 200 + 10 + 3 – 200 = 13
Из 2 стопок по 100 палочек, 1 стопке с 10 палочками и 3 палочек вычли 2 стопки по 100 палочек, получилось 13 палочек.
213 – 3 = 200 + 10 + 3 – 3 = 210
Из 2 стопок по 100 палочек, 1 стопки с 10 палочками и 3 палочек вычли 3 палочки, получилось 210 палочек.
Оформляем задание в тетрадь.
200 + 10 + 3 = 2 сот. + 1 дес. + 3 ед. = 213
213 = 2 сот. + 1 дес. + 3 ед. = 200 + 10 + 3
200 + 13 = 2 сот. + 1 дес. + 3 ед. = 200 + 10 + 3 = 213
210 + 3 = 2 сот. + 1 дес. + 3 ед. = 200 + 10 + 3 = 213
203 + 10 = 2 сот. + 1 дес. + 3 ед. = 200 + 3 + 10 = 213
213 – 10 = 2 сот. + 1 дес. + 3 ед. – 1 дес. = 2 сот. + 0 дес. + 3 ед. = 203
213 – 13 = 2 сот. + 1 дес. 3 ед. – 1 дес. 3 ед. = 2 сот. = 200
213 – 200 = 2 сот. + 1 дес. 3 ед. – 2 сот. = 13
213 – 3 = 2 сот. + 1 дес. + 3 ед. – 3 ед. = 2 сот. + 1 дес. = 210
Задание внизу страницы
Ответ:590 = 500 + 90 208 = 200 + 8 367 = 300 + 60 + 7
1) Вспомни, как образуются и называются трёхзначные числа.
2) Повтори, как разложить число на разрядные слагаемые.
Рассуждаем.
590 – число состоит из 5 сот. и 9 дес.
590 = 5 сот. + 9 дес. + 0 дес. = 500 + 90
Разряд единиц отсутствует.
208 – число состоит из 2 сот. и 8 ед.
208 = 2 сот. + 0 дес. + 8 ед. = 200 + 8
Разряд десятков отсутствует.
367 – число состоит из 3 сот., 6 дес. и 7 ед.
367 = 3 сот. + 6 дес. + 7 ед. = 300 + 60 + 7
Все разряды присутствуют.
Оформляем задание в тетрадь.
590 = 500 + 90
208 = 200 + 8
367 = 300 + 60 + 7
Задание на полях страницы.
Вычисли значения выражений. Разбей выражения на 2 группы разными способами.
56 : 8 9 · 6 56 : 7 6 · 9 8 · 7 54 : 9 7 · 8 54 : 6
Ответ:Первая группа (по действию)
56 : 8 = 7 9 · 6 = 54
56 : 7 = 8 6 · 9 = 54
54 : 9 = 6 8 · 7 = 56
54 : 6 = 9 7 · 8 = 56
Вторая группа (по одинаковой сумме значений)
6 · 9 = 54
9 · 6 = 54
54 : 6 = 9
54 + 54 + 9 + 8 = 125
7 · 8 = 56
8 · 7 = 56
54 : 9 = 6
56 : 8 = 7
56 + 56 + 6 + 7 = 125
По числам, используемым в выражениях
(7, 8, 56)
56 : 8 = 7
56 : 7 = 8
8 · 7 = 56
7 · 8 = 56
(6, 9, 54)
54 : 9 = 6
54 : 6 = 9
6 · 9 = 54
9 · 6 = 54
Чтобы разделить выражения на две группы, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Вычислим значения выражения.
56 : 8 = 7
9 ∙ 6 = 54
56 : 7 = 8
6 ∙ 9 = 54
8 ∙ 7 = 56
54 : 9 = 6
7 ∙ 8 = 56
54 : 6 = 9
Рассуждаем.
1 способ разбития на группы: по действиям.
Деление Умножение
56 : 8 = 7 9 ∙ 6 = 54
56 : 7 = 8 6 ∙ 9 = 54
54 : 9 = 6 8 ∙ 7 = 56
54 : 6 = 9 7 ∙ 8 = 56
2 способ разбития на группы: по использованным числам в выражении.
Числа 56, 8, 7 Числа 54, 9, 6
56 : 8 = 7 9 ∙ 6 = 54
56 : 7 = 8 6 ∙ 9 = 54
8 ∙ 7 = 56 54 : 9 = 6
7 ∙ 8 = 56 54 : 6 = 9
Оформляем задание в тетрадь.
1) 1 группа:
56 : 8 = 7
56 : 7 = 8
54 : 9 = 6
54 : 6 = 9
2 группа:
9 ∙ 6 = 54
6 ∙ 9 = 54
8 ∙ 7 = 56
7 ∙ 8 = 56
2) 1 группа:
56 : 8 = 7
56 : 7 = 8
8 ∙ 7 = 56
7 ∙ 8 = 56
2 группа:
9 ∙ 6 = 54
6 ∙ 9 = 54
54 : 9 = 6
54 : 6 = 9
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.