Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 35

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 15.
Найди на рисунке прямые, острые и тупые углы. Выпиши их номера.

Прямые углы: 8, 9, 10, 11, 13, 14, 12, 15. Острые углы: 1, 2, 3, 4, 6. Тупые углы: 5, 7.
1) Чтобы узнать название угла, сравнивай каждый угол с прямым углом.
2) Тупой угол – больше 90º;
3) Прямой угол – равен 90º;
4) Острый угол – меньше 90º.
Рассуждаем.
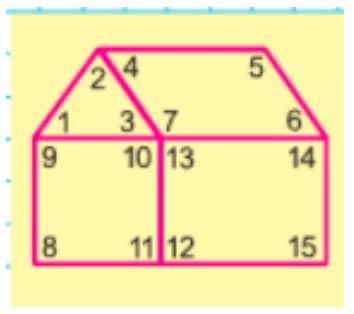
Рассмотрим углы.
1 – меньше прямого, значит острый;
2 - меньше прямого, значит острый;
3 - меньше прямого, значит острый;
4 - меньше прямого, значит острый;
5 – больше прямого, значит тупой;
6 - меньше прямого, значит острый;
7 - больше прямого, значит тупой;
8 – прямой угол;
9 - прямой угол;
10 - прямой угол;
11 - прямой угол;
12 - прямой угол;
13 - прямой угол;
14 - прямой угол;
15 - прямой угол;
Делаем вывод.
Прямые углы: 8, 9, 10, 11, 12, 13, 14, 15.
Острые углы: 1, 2, 3, 4, 6.
Тупые углы: 5, 7.
Номер 16.
Выполни деление с остатком.
Ответ:36 : 7 = 5 (ост. 1) 44 : 5 = 8 (ост. 4) 60 : 8 = 7 (ост. 4) 80 : 12 = 6 (ост. 8) 44 : 18 = 2 (ост. 8)
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
36 : 7 = 5 (ост. 1)
36 не делится на 7 без остатка. Вспомним, какое самое большое число до 36 делится на 7 без остатка. Это 35.
Найдём частное: 35 : 7 = 5.
Найдём остаток: 36 − 35 = 1.
44 : 5 = 8 (ост. 4)
44 не делится на 5 без остатка. Вспомним, какое самое большое число до 44 делится на 5 без остатка. Это 40.
Найдём частное: 40 : 5 = 8.
Найдём остаток: 44 − 40 = 4.
60 : 8 = 7 (ост. 4)
60 не делится на 8 без остатка. Вспомним, какое самое большое число до 60 делится на 8 без остатка. Это 56.
Найдём частное: 56 : 8 = 7.
Найдём остаток: 60 − 56 = 4.
80 : 12 = 6 (ост. 8)
Если трудно вспомнить самое большое число до 80, которое делится на 12 без остатка, то частное можно найти способом подбора.
Надо 80 разделить на 12.
Пробуем в частном 5.
Проверим: 12 ∙ 5 = 60.
Найдём остаток и сравним его с делителем: 80 − 60 = 20, 20 > 12, значит 5 мало.
Пробуем в частном 6.
Проверим: 12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72.
Найдем остаток и сравним его с делителем: 80 − 72 = 8, 8 < 12, значит частное 6, а остаток 8.
44 : 18 = 2 (ост. 8)
Если трудно вспомнить самое большое число до 44, которое делится на 18 без остатка, то частное можно найти способом подбора.
Надо 44 разделить на 18.
Пробуем в частном 2.
Проверим: 18 ∙ 2 = (10 + 8) ∙ 2 = 20 + 16 = 36.
Найдём остаток и сравним его с делителем: 44 − 36 = 8, 8 < 18, значит частное 2, а остаток 8.
Оформляем задание в тетрадь.
36 : 7 = 5 (ост. 1)
Проверка: 5 ∙ 7 + 1 = 35 + 1 = 36
1 < 7
44 : 5 = 8 (ост. 4)
Проверка: 8 ∙ 5 + 4 = 40 + 4 = 44
4 < 5
60 : 8 = 7 (ост. 4)
Проверка: 7 ∙ 8 + 4 = 56 + 4 = 60
4 < 8
80 : 12 = 6 (ост. 8)
Проверка: 6 ∙ 12 + 8 = 72 + 8 = 80
8 < 12
44 : 18 = 2 (ост. 8)
Проверка: 18 ∙ 2 + 8 = 36 + 8 = 44
8 < 18
Номер 17.
Запиши по 3 числа, при делении которых на 8 в остатке получается 5; 6; 2; 0.
Ответ:29 : 8 = 3 (ост. 5)
45 : 8 = 5 (ост. 5)
61 : 8 = 7 (ост. 5)
22 : 8 = 2 (ост. 6)
38 : 8 = 4 (ост. 6)
54 : 8 = 6 (ост. 6)
18 : 8 = 2 (ост. 2)
58 : 8 = 7 (ост. 2)
82 : 8 = 10 (ост. 2)
16 : 8 = 2 (ост. 0)
64 : 8 = 8 (ост. 0)
72 : 8 = 9 (ост. 0)
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
Чтобы найти число, которое при делении на 8 в остатке было 5, нужно к числу, которое без остатка делится на 8 прибавить 5.
13 : 8 = 1 (ост. 5)
21 : 8 = 2 (от. 5)
37 : 8 = 4 (ост. 5)
Чтобы найти число, которое при делении на 8 в остатке было 6, нужно к числу, которое без остатка делится на 8 прибавить 6.
14 : 8 = 1 (ост. 6)
30 : 8 = 3 (ост. 6)
46 : 8 = 5 (ост. 6)
Чтобы найти число, которое при делении на 8 в остатке было 2, нужно к числу, которое без остатка делится на 8 прибавить 2.
18 : 8 = 2 (ост. 2)
34 : 8 = 3 (ост. 2)
50 : 8 = 6 (ост. 2)
Если в остатке 0, значит число делится без остатка.
8 : 8 = 1 (ост. 0)
24 : 8 = 3 (ост. 0)
40 : 8 = 5 (ост. 0)
Оформляем задание в тетрадь.
Числа, при делении которых на 8 в остатке получается 5 – 13, 21, 37.
Числа, при делении которых на 8 в остатке получается 6 – 14, 30, 46.
Числа, при делении которых на 8 в остатке получается 2 – 18, 34, 50.
Числа, при делении которых на 8 в остатке получается 0 – 8, 24, 40.
Номер 18.
Выйдет ли квадратная проволочная рамка со стороной 7 см из треугольной рамки, каждая сторона которой равна 9 см?
Ответ:Квадратная проволочная рамка со стороной 7 см. Треугольная проволочная рамка со стороной 9 см. Р(тр) = 9 + 9 + 9 Р(тр) = 27 см. Периметр проволочного квадратной рамки со стороной 7 см. – 7 · 4 7 · 4 = 28 см., а 27 < 28, по этому проволоки от треугольной рамки не хватит. Ответ: квадратной проволочной рамки не выйдет из треугольной, потому что проволоки не хватит.
1) Треугольник – это фигура, у которой 3 стороны;
2) Квадрат – это фигура, у которой 4 стороны.
Рассуждаем.
Длина ломанной – это сумма длин всех его отрезков, то есть периметр. Чтобы найти периметр треугольника, нужно все его три стороны сложить. Но у данного треугольника все стороны равны, значит сложение одинаковых слагаемых можно заменить умножением.
9 ∙ 3 = 27 (см) – периметр треугольника или длина проволоки.
Продолжаем рассуждение.
Длина ломанной – это сумма длин всех его отрезков, то есть периметр. Чтобы найти периметр квадрата, нужно все его 4 стороны сложить. У квадрата все стороны равны, значит сложение одинаковых слагаемых можно заменить умножением.
27 : 7 = 3 (ост. 6) – на сколько хватит сторон длинна которой 7 см.
Хватит на 3 стороны и останется 6 см. Так как в квадрате 4 стороны, то на квадрат со стороной 7 см проволоки не хватит.
Записываем ответ.
Ответ: нет, не выйдет.
Номер 19.
На юношеских соревнованиях по плаванию на 100 м Косте осталось проплыть четвертую часть дистанции, а Вите – пятую ее часть. Кто из них ближе к финишу и на сколько метров?
Ответ:
1) 100 : 4 = 25 (м) – осталось проплыть Косте.
2) 100 : 5 = 20 (м) – осталось проплыть Вите.
3) 25 – 20 = 5 (м) – на столько ближе Витя.
Ответ: Витя ближе Кости к финишу на 5 м.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического рисунка.
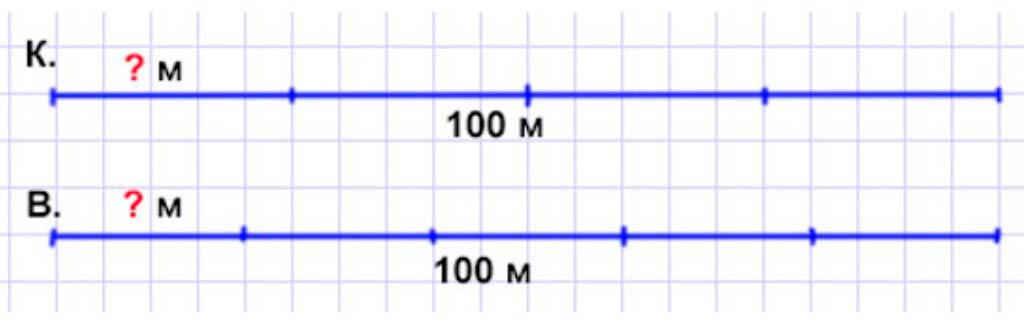
Рассуждаем.
Косте осталось проплыть четвертую часть дистанции.
Одна четвертая часть обозначает, что целое число разделили на 4 части и взяли одну такую часть.
Чтобы узнать сколько Косте осталось проплыть, нужно полную длину дистанции разделить на 4.
100 : 4 = (80 + 20) : 4 = 20 + 5 = 25 (м) – осталось проплыть Кости.
Продолжаем рассуждение.
Витя осталось проплыть пятую часть дистанции.
Одна пятая часть обозначает, что целое число разделили на 5 частей и взяли одну такую часть.
Чтобы узнать сколько Вите осталось проплыть, нужно полную длину дистанции разделить на 5.
100 : 5 = 10 дес. : 5 = 2 дес. = 20 (м) – осталось проплыть Вите.
Продолжаем рассуждение.
Сравниваем показатели. У кого меньше показатель, значит тому меньше плыть до финиша, значит он ближе к финишу.
25 м > 20 м – значит Витя ближе к финишу, чем Костя.
25 – 20 = 5 (м) – на сколько ближе Витя, чем Костя к финишу.
Записываем ответ.
Ответ: Витя ближе к финишу на 5 м.
Номер 20.
Ответ:7 м 8 дм = 78 дм, потому что 78 дм = 78 дм 95 см > 8 дм 9 см, потому что 95 см > 89 см 6 дм 5 см < 7 дм, потому что 65 см < 70 см 18 мм = 1 см 8 мм, потому что 18 мм = 18 мм
Помни, что сравнивать числовые значения длины можно только если они выражены в одних единицах измерения:
1 см = 10 мм
1 дм = 10 см
Рассуждаем.
Сравним 7 м 8 дм и 78 дм
Переведём 7 м 8 дм в дециметры:
7 м 8 дм = 7 ∙ 10 дм + 8 дм = 78 дм
Так как 78 дм = 78 дм, значит 7 м 8 дм = 78 дм
Ставим знак равно.
Сравним 6 дм 5 см и 7 дм
6 дм 5 см < 7 дм, так как 6 дм < 7 дм
Ставим знак меньше.
Сравним 95 см и 8 дм 9 см
Переведём 8 дм 9 см в сантиметры:
8 дм 9 см = 8 ∙ 10 см + 9 см = 89 см
Так как 95 см > 89 см, значит 95 см > 8 дм 9 см
Ставим знак больше.
Сравним 18 мм и 1 см 8 мм
Переведём 1 см 8 мм в миллиметры:
1 см 8 мм = 1 ∙ 10 мм + 8 мм = 18 мм
Так как 18 мм = 18 мм, значит 18 мм = 1 см 8 мм
Ставим знак равно.
Запишем решение в тетрадь.
7 м 8 дм = 78 дм, так как 78 дм = 78 дм
6 дм 5 см < 7 дм, так как 6 дм < 7 дм
95 см > 8 дм 9 см, так как 95 см > 89 см
18 мм = 1 см 8 мм, так как 18 мм = 18 мм
Номер 21.
Что больше и на сколько:
Ответ:1) 45 : 9 < 42 : 6 8 ∙ 8 > 9 ∙ 7
42 : 6 – 45 : 9 = 2 8 ∙ 8 – 9 ∙ 7 = 1
2) 18 : 2 > 27 : 9 56 : 7 > 24 : 6
18 : 2 – 27 : 9 = 6 56 : 7 – 24 : 6 = 4
1) Прежде, чем сравнить выражения, вычисли их значения в левой и правой части.
2) Помни о том, что сравнивать численных значения длины можно только, если они выражены в одних единицах измерения.
Рассмотрим выражения.
Сравним 45 : 9 и 42 : 6
Вычислим левую часть 45 : 9 = 5
Вычислим правую часть 42 : 6 = 7
Сравним 5 < 7
Вычислим на сколько больше 7 – 5 = 2
Значит, 42 : 6 > 45 : 9 на 2.
Сравним 18 : 2 и 27 : 9
Вычислим левую часть 18 : 2 = 9
Вычислим правую часть 27 : 9 = 3
Сравним 9 > 3
Вычислим на сколько больше 9 – 3 = 6
Значит, 18 : 2 > 27 : 9 на 6.
Сравним 8 ∙ 8 и 9 ∙ 7
Вычислим левую часть 8 ∙ 8 = 64
Вычислим правую часть 9 ∙ 7 = 63
Сравним 64 > 63
Вычислим на сколько больше 64 – 63 = 1
Значит, 8 ∙ 8 > 9 ∙ 7 на 1.
Сравним 56 : 7 и 24 : 6
Вычислим левую часть 56 : 7 = 8
Вычислим правую часть 24 : 6 = 4
Сравним 8 > 4
Вычислим на сколько больше 8 – 4 = 4
Значит, 56 : 7 > 24 : 6 на 4.
Запишем решение в тетрадь.
1) 45 : 9 < 42 : 6
45 : 9 = 5
42 : 6 = 7
Выражение 42 : 6 больше выражения 45 : 9 на 2.
2) 18 : 2 > 27 : 9
18 : 2 = 9
27 : 9 = 3
Выражение 18 : 2 больше выражения 27 : 9 на 6.
3) 8 ∙ 8 > 9 ∙ 7
8 ∙ 8 = 64
9 ∙ 7 = 63
Выражение 8 ∙ 8 больше выражения 9 ∙ 7 на 1.
4) 56 : 7 > 24 : 6
56 : 7 = 8
24 : 6 = 4
Выражение 56 : 7 больше выражения 24 : 6 на 4.
Номер 22.
Ответ:
99 : 9 + 32 : 2 = 11 + 16 = 27 96 : 8 + 75 : 5 = 12 + 15 = 27
1) Вспомни, как выполняется деление методом подбора.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Выполним деление с помощью правила деления суммы на число:
72 : 4 = (40 + 32) : 4 = 40 : 4 + 32 : 4 = 10 + 8 = 18
Представим число 72 в виде суммы 40 и 32, каждое слагаемое разделим на 4 и полученные результаты сложим.
96 : 3 = (90 + 6) : 3 = 90 : 3 + 6 : 3 = 30 + 2 = 32
Представим число 96 в виде суммы 90 и 6, каждое слагаемое разделим на 3 и полученные результаты сложим.
Выполним деление методом подбора.
51 : 17 = ?
Нужно 51 разделить на 17.
Пробуем в частном 2 и проверяем: 17 ∙ 2 = 34, 34 < 51, число 2 не подходит.
Пробуем в частном 3 и проверяем: 17 ∙ 3 = 51, 51 = 51, число 3 подходит.
Значит 51 : 17 = 3.
54 : 18 = ?
Нужно 54 разделить на 18.
Пробуем в частном 2 и проверяем: 18 ∙ 3 = 36, 36 < 54, число 2 не подходит.
Пробуем в частном 3 и проверяем: 18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54, 54 = 54, число 3 подходит.
Значит 54 : 18 = 3.
98 : 14 = ?
Нужно 98 разделить на 14.
Пробуем в частном 6 и проверяем: 14 ∙ 6 = (10 + 4) ∙ 6 = 60 + 24 = 84, 84 < 98, число 6 не подходит.
Пробуем в частном 7 и проверяем: 14 ∙ 7 = (10 + 4) ∙ 7 = 70 + 28 = 98, 98 = 98, число 7 подходит.
Значит 98 : 14 = 7.
84 : 12 = 7
Нужно 84 разделить на 12.
Пробуем в частном 6 и проверяем: 12 ∙ 6 = 72, 72 < 84, число 6 не подходит.
Пробуем в частном 7 и проверяем: 12 ∙ 7 = 84, 84 = 84, число 7 подходит.
Значит 84 : 12 = 7.
Выполним вычисления по действиям.
99 : 9 + 32 : 2 = 27
1) 99 : 9 = 11
2) 32 : 2 = (20 + 12) : 2 = 20 : 2 + 12 : 2 = 10 + 6 = 16
3) 11 + 16 = 27
96 : 8 + 75 : 5 = 27
1) 96 : 8 = (80 + 16) : 8 = 80 : 8 + 16 : 8 = 10 + 2 = 12
2) 75 : 5 = (50 + 25) : 5 = 50 : 5 + 25 : 5 = 10 + 5 = 15
3) 12 + 15 = 27
Запишем решение в тетрадь.
72 : 4 = (40 + 32) : 4 = 10 + 8 = 18
96 : 3 = (90 + 6) : 3 = 30 + 2 = 32
51 : 17 = 3, так как 17 ∙ 3 = (10 + 7) ∙ 3 = 30 + 21 = 51
54 : 18 = 3, так как 18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54
98 : 14 = 7, так как 14 ∙ 7 = (10 + 4) ∙ 7 = 70 + 28 = 98
84 : 12 = 7, так как 12 ∙ 7 = (10 + 2) ∙ 7 = 70 + 14 = 84
99 : 9 + 32 : 2 = 11 + 16 = 27
96 : 8 + 75 : 5 = 12 + 15 = 27
Номер 23.
1) Ломаная состоит из четырех одинаковых звеньев, длиной 3 см каждое. Найди длину этой ломаной. 2) Начерти ломаную такой же длины, но состоящую из трех звеньев одной длины; разной длины.
Ответ:1) 4 ∙ 3 = 12 (см) – длина ломаной. Ответ: общая длина ломаной составляет 12 см.

2)

1) Ломаная линия – геометрическая фигура, состоящая из звеньев-отрезков, не лежащих на одной прямой.
2) Длина ломаной – сумма длин всех его отрезков.
Рассуждаем.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины. Но длина каждого отрезка одинаковы, значит сумму одинаковых слагаемых можно заменить умножением.
3 см ∙ 4 = 12 см – длина ломанной.
Записываем ответ.
Ответ: 12 см.
Рассуждаем.
Общая длина ломанной равна 12 см и она разделена на 3 одинаковые звена. Значит, чтобы найти длину одного звена нужно общую длину ломанной разделить на количество звеньев.
12 см : 3 = 4 см – длина каждого звена одной длины.
Начертим.
Начертим ломанную, состоящую из трёх одинаковых звеньев, длиной 4 см каждая.
.jpg)
Продолжаем рассуждение.
Возможные варианты ломанной длина, которой 12 см и звенья разной длины.
12 см = 1 см + 2 см + 9 см
12 см = 2 см + 3 см + 7 см
12 см = 3 см + 4 см + 5 см
12 см = 1 см + 5 см + 6 см
Начертим.
Начертим такие ломанные.
.jpg)
Номер 24.
Начерти в тетради пятиугольник, в котором будет 2 прямых угла, 2 тупых и 1 острый угол.
Ответ:
1) Тупой угол – больше 90º;
2) Прямой угол – равен 90º;
3) Острый угол – меньше 90º.
Рассуждаем.
Вспомним виды углов:
Прямой угол – это угол в 90 (90 градусов).
Острый угол – это угол, который меньше прямого угла, меньше 90.
Тупой угол – это угол, который больше прямого угла, больше 90.
Начертим такую фигуру.
Нужно начертить фигуру в которой есть 2 прямых угла, 2 тупых угла и 1 острый угол.
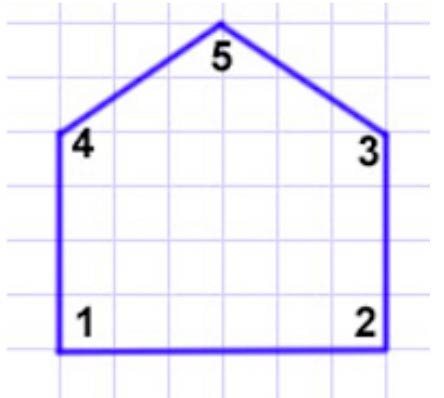
Рассмотрим фигуру.
Углы 1 и 2 – прямые углы.
Углы 4 и 5 – тупые углы.
Угол 5 – острый угол.
Номер 25.
Переставь карточки так, чтобы равенство стало верным.

96 : 4 = 24
Внимательно рассмотри карточки и составь верные равенства (примеры).
Рассуждаем.
Рассмотрим выражение.
Если внимательно посмотреть, то если поменять карточку 9 поставить перед карточкой 6, а карточку 4 после карточки 2, то получится верное равенство 96 : 24 = 4.
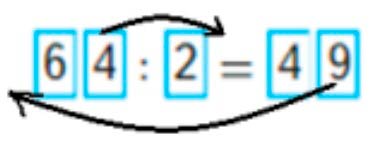
Также возможен второй вариант:
96 : 4 = 24
Выполним проверку.
96 : 24 = ?
Выполним вычисление методом подбора.
Нужно 96 разделить на 24.
Пробуем в частном 3 и проверяем: 24 ∙ 3 = (20 + 4) ∙ 3 = 60 + 12 = 72, 72 < 96, число 3 не подходит.
Пробуем в частном 4 и проверяем: 24 ∙ 4 = (20 + 4) ∙ 4 = 80 + 16 = 96, 96 = 96, число 4 подходит.
Значит 96 : 24 = 4.
96 : 4 = (80 + 16) : 4 = 20 + 4 = 24
Представим число 96 в виде суммы 80 и 16, разделим каждое слагаемое на 4 и полученные значения сложим.
Оформляем задание в тетрадь.
96 : 24 = 4 или 96 : 4 = 24.
Номер 26.
Найди разными способами площадь данной фигуры.


1) Чтобы вычислить площадь фигуры, нужно понять, какую часть плоскости она занимает в единицах квадратных единицах измерения.
2) Но у фигур сложных, т.е. у которых площадь нельзя вычислить по формуле, нужно поступать иначе. У сложных фигур площадь фигуры равна сумме площадей фигур, из которых она состоит.
Вычисляем.
Вычислим площадь фигуры.
Способ решения 1.
Разделим фигуру на 3 равных прямоугольника.
Получится 3 равных прямоугольника со сторонами 1 см и 2 см.
.jpg)
Чтобы найти площадь одного прямоугольника нужно длину умножить на ширину.
1) 1 см ∙ 2 см = 2 см2 – площадь одного прямоугольника.
Площадь каждого прямоугольника одинаковы, значит, чтобы найти площадь всех 3 прямоугольников, нужно площадь одного такого прямоугольника умножить на количество прямоугольников.
2) 2 см2 ∙ 3 = 6 см2 – площадь всей фигуры.
Ответ: 6 см2
Способ решения 2.
Разделим данную фигуру на 6 одинаковых квадратов. Сторона каждого квадрата равна 1 см.
.jpg)
Чтобы вычислить площадь квадрата, нужно длину умножить на ширину.
1) 1 см ∙ 1 см = 1 см2 – площадь одного квадрата
Площадь квадратов равны, значит, чтобы найти площадь всех 6 квадратов, нужно площадь одного такого квадрата умножить на количество квадратов.
2) 1 см2 ∙ 6 = 6 см2 – площадь всей фигуры.
Ответ: 6 см2
Способ решения 3.
Дочертим фигуру до квадрата, найдем его площадь и вычтем площадь лишних фигур (трёх маленьких квадратов).
Длина большого квадрата – 3 см, длина маленького квадрата – 1 см.
.jpg)
Найдём площадь большого квадрата, умножив длину на ширину.
1) 3 см ∙ 3 см = 9 см2 – площадь большого квадрата.
Найдём площадь маленького квадрата, умножив длину на ширину.
2) 1 см ∙ 1 см = 1 см2 – площадь 1 маленького квадрата
Найдём площадь 3 маленьких квадратов, умножив площадь одного такого квадрата на 3.
3) 1 см2 ∙ 3 = 3 см2 – площадь 3 маленьких квадратов.
Найдём площадь фигуры, для этого из большого квадрата вычтем площадь 3 маленьких квадратов.
4) 9 см2 − 3 см2 = 6 см2 – площадь данной фигуры.
Ответ: 6 см2.
Выполним задание.
Начертим такую фигуру и найдём ось симметрии.
Ось симметрии – линия, по которой можно сложить фигуру так, что части совпадут при перегибании, т.е. наложении.
У фигуры одна ось симметрии (синяя линия).
.jpg)
Если фигуру сложить по синей линии, то правая часть совпадёт с левой её частью.
Номер 15.
Найди на рисунке прямые, острые и тупые углы. Выпиши их номера.

Прямые углы: 8, 9, 10, 11, 13, 14, 12, 15. Острые углы: 1, 2, 3, 4, 6. Тупые углы: 5, 7.
Номер 16.
Выполни деление с остатком.
Ответ:36 : 7 = 5 (ост. 1) 44 : 5 = 8 (ост. 4) 60 : 8 = 7 (ост. 4) 80 : 12 = 6 (ост. 8) 44 : 18 = 2 (ост. 8)
Номер 17.
Запиши по 3 числа, при делении которых на 8 в остатке получается 5; 6; 2; 0.
Ответ:29 : 8 = 3 (ост. 5)
45 : 8 = 5 (ост. 5)
61 : 8 = 7 (ост. 5)
22 : 8 = 2 (ост. 6)
38 : 8 = 4 (ост. 6)
54 : 8 = 6 (ост. 6)
18 : 8 = 2 (ост. 2)
58 : 8 = 7 (ост. 2)
82 : 8 = 10 (ост. 2)
16 : 8 = 2 (ост. 0)
64 : 8 = 8 (ост. 0)
72 : 8 = 9 (ост. 0)
Номер 18.
Выйдет ли квадратная проволочная рамка со стороной 7 см из треугольной рамки, каждая сторона которой равна 9 см?
Ответ:Квадратная проволочная рамка со стороной 7 см. Треугольная проволочная рамка со стороной 9 см. Р(тр) = 9 + 9 + 9 Р(тр) = 27 см. Периметр проволочного квадратной рамки со стороной 7 см. – 7 · 4 7 · 4 = 28 см., а 27 < 28, по этому проволоки от треугольной рамки не хватит. Ответ: квадратной проволочной рамки не выйдет из треугольной, потому что проволоки не хватит.
Номер 19.
На юношеских соревнованиях по плаванию на 100 м Косте осталось проплыть четвертую часть дистанции, а Вите – пятую ее часть. Кто из них ближе к финишу и на сколько метров?
Ответ:
1) 100 : 4 = 25 (м) – осталось проплыть Косте.
2) 100 : 5 = 20 (м) – осталось проплыть Вите.
3) 25 – 20 = 5 (м) – на столько ближе Витя.
Ответ: Витя ближе Кости к финишу на 5 м.
Номер 20.
Ответ:7 м 8 дм = 78 дм, потому что 78 дм = 78 дм 95 см > 8 дм 9 см, потому что 95 см > 89 см 6 дм 5 см < 7 дм, потому что 65 см < 70 см 18 мм = 1 см 8 мм, потому что 18 мм = 18 мм
Номер 21.
Что больше и на сколько:
Ответ:1) 45 : 9 < 42 : 6 8 ∙ 8 > 9 ∙ 7
42 : 6 – 45 : 9 = 2 8 ∙ 8 – 9 ∙ 7 = 1
2) 18 : 2 > 27 : 9 56 : 7 > 24 : 6
18 : 2 – 27 : 9 = 6 56 : 7 – 24 : 6 = 4
Номер 22.
Ответ:
99 : 9 + 32 : 2 = 11 + 16 = 27 96 : 8 + 75 : 5 = 12 + 15 = 27
Номер 23.
1) Ломаная состоит из четырех одинаковых звеньев, длиной 3 см каждое. Найди длину этой ломаной. 2) Начерти ломаную такой же длины, но состоящую из трех звеньев одной длины; разной длины.
Ответ:1) 4 ∙ 3 = 12 (см) – длина ломаной. Ответ: общая длина ломаной составляет 12 см

2)

Номер 24.
Начерти в тетради пятиугольник, в котором будет 2 прямых угла, 2 тупых и 1 острый угол.
Ответ:
Номер 25.
Переставь карточки так, чтобы равенство стало верным.

96 : 4 = 24
Номер 26.
Найди разными способами площадь данной фигуры. Начерти такую фигуру и проведи в ней ось симметрии.


Ось симметрии:

Задание 1.
Прочитаем рассказ Н. Н. Носова «Мишкина каша». Какие ошибки допустили мальчики в задачах расчетах?
Ответ:1) В сказке мальчики не знали, сколько к одной части каши взять частей воды. 2) Не учитывали время приготовления каши.
Задание 2.
Прочитаем стихотворение С. В. Михалкова «Жадный Вартан» (армянская сказка).
Ответ:Ошибка в задаче расчётах: 1) Не рассчитал количество шкуры, которая необходима на пошив шапки нужного размера. 2) Если одну шкуру разделить на большее количество частей, то шапки получатся маленькими.
Задание 3.
Узнайте у своих близких (в своей семье, у родственников, у знакомых), какие задачи-расчёты им приходится решать, какие трудности они испытывают при решении, где узнают необходимые сведения для правильных расчётов.
Ответ:Задачи-расчёты которые приходится решать взрослым:
– рассчитать путь от дома до работы;
– рассчитать количество продуктов на неделю;
– рассчитать сколько нужно обоев для ремонта комнаты и т. д.
Трудности: не верные подсчеты.
Сведения для правильных подсчетов: на упаковке, в интернете.
Темы проектов
Проект 1.
Тема «Затраты времени на занятия в школе по дням недели, в том числе и на дополнительные занятия в кружках, секциях и т. п.»
Ответ:1) Задача проекта: рассчитать затраты времени на занятия в школе по дням недели, в том числе и на дополнительные занятия в кружках;
2) Срок выполнения работы: 1 неделя.
План работы
1) Составим список занятий;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод о том сколько необходимо времени на занятия на каждый день недели.
1) Задача проекта: рассчитать затраты времени на занятия в школе по дням недели, в том числе и на дополнительные занятия в кружках;
2) Срок выполнения работы: 1 неделя.
Составим план.
1) Составим список занятий;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
Составим список.
Список занятий:
– Уроки в школе с переменой;
– Плавание;
– Шахматы;
– Лего.
Список занятий запишем в таблицу по дням недели и будем заполнять её в течении недели.
Выполняя занятия, записывай сколько ты тратишь на это время каждый день.
-(2024).jpg)
Оформим проект.
Оформим проект в виде таблицы.
Всю неделю мы должны были записывать сколько потратили время на занятия и оформить проект в виде таблицы.
По истечении недели мы вычислим общее время, которое потратили на занятия.
-(2024).jpg)
Рассчитаем.
Посчитаем сколько тратится времени на выполнение каждого занятия за неделю.
1) Уроки в школе:
4 ч + 4 ч 45 мин + 4 ч + 4 ч 45 мин + 4 ч 45 мин = 22 ч 15 мин
2) Плавание:
1 ч + 1 ч = 2 ч
3) Шахматы:
45 мин + 45 мин = 90 мин = 1 ч 30 мин
4) Лего:
45 мин + 45 мин = 90 мин = 1 ч 30 мин
5) Общее время, потраченное на занятия за неделю:
22 ч 15 мин + 2 ч + 1 ч 30 мин + 1 ч 30 мин = 24 ч 15 мин + 3 ч = 27 ч 15 мин
Делаем вывод.
Вывод: На все занятия в школе том числе и занятия в кружках за неделю было потрачено 27 ч 15 мин.
-(2024).jpg)
Проект 2.
Тема «Затраты времени на постоянные домашние дела за 1 неделю».
Ответ:1) Задача проекта: рассчитать затраты времени на постоянные домашние дела;
2) Срок выполнения работы: 1 неделя.
План работы
1) Составим список домашних дел;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод о том сколько необходимо времени на постоянные домашние дела.
1) Задача проекта: рассчитать затраты времени на постоянные домашние дела;
2) Срок выполнения работы: 1 неделя.
Составим план.
1) Составим список домашних дел;
2) Собрать нужную информацию;
3) Оформить проект;
4) Сделать вывод.
Составим список домашних дел и соберём нужную информацию.
Список домашних дел:
– Помощь взрослым;
– Уход за домашними растениями;
– Уход за животными;
– Уборка комнаты;
– Мытье посуды.
Список домашних дел запишем в таблицу по дням недели и будем заполнять её в течении недели.
Выполняя домашние дела, записывай сколько ты тратишь на это время каждый день.
-(2024).jpg)
Оформим проект.
Оформим проект в виде таблицы.
Всю неделю мы должны были записывать сколько потратили время на домашние дела. И оформить проект в виде таблицы.
По истечении недели мы вычислим общее время, которое потратили на домашние дела.
-(2024).jpg)
Рассчитаем.
Посчитаем сколько тратится времени на выполнение каждой работы за неделю.
1) Помощь взрослым:
30 мин + 30 мин + 30 мин + 30 мин + 30 мин + 1 час + 1 час = 4 часа 30 мин.
2) Уход за домашними растениями:
10 мин + 10 мин + 10 мин + 10 мин = 40 мин.
3) Уход за животными:
20 мин + 10 мин + 20 мин + 10 мин + 20 мин + 10мин + 30 мин = 2 часа.
4) Уборка комнаты:
15 мин + 15 мин + 15 мин + 15 мин + 15 мин + 1 час = 2 часа 15 мин.
5) Мытье посуды:
5 мин + 5 мин + 5 мин + 5 мин + 5 мин + 5 мин + 5 мин = 35 мин.
6) Общее время, потраченное на домашние дела за неделю:
4 ч 30 мин + 40 мин + 2 ч + 2 ч 15 мин + 35 мин = 10 ч.
Делаем вывод.
Вывод: На все домашние дела за неделю было потрачено 10 часов.
Проект 3.
Тема «Затраты времени на разные виды отдыха (прогулки, экскурсии, посещение театров, музеев, чтение книг, просмотр телевизионных передач и др.) в течение 1 месяца.».
Ответ:1) Задача проекта: рассчитать затраты времени на разные виды отдыха;
2) Срок выполнения работы: 1 месяц.
План работы
1) Составим список видов отдыха;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод о том сколько необходимо времени на разные виды отдыха.
1) Задача проекта: рассчитать затраты времени на разные виды отдыха;
2) Срок выполнения работы: 1 месяц.
Составим план.
1) Составим список видов отдыха;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
Составим список видов отдыха и соберём нужную информацию.
Список видов отдыха:
– Прогулка;
– Чтение книг;
– Просмотр телевизора или игра в компьютер;
– Культурно-просветительный поход (театр; музей; кинотеатр и др.)
Список видов отдыха запишем в таблицу по неделям и будем заполнять её в течении месяца.
В течения месяца записывай сколько тратится времени на отдых.
-(2024).jpg)
Оформим проект.
Оформим проект в виде таблицы.
Весь месяц мы должны были записывать сколько потратили время на досуг. И оформить проект в виде таблицы.
По истечении месяца мы вычислим общее время, которое потратили на досуг.
-(2024).jpg)
Рассчитаем.
Посчитаем сколько тратится времени на досуг за месяц.
1) Прогулка:
Каждый день примерно гуляли по 1 ч в день. Значит прогулка занимала 7 ч за неделю, а в месяц – 28 часов.
1 ч ∙ 7 = 7 ч – за неделю;
7 ч ∙ 4 = 28 ч – за месяц.
2) Чтение книг:
Каждый день примерно читали по 40 минут в день. Значит, чтение книг заняло 4 ч 40 минут за неделю, а за месяц – 18 ч 40 минут.
40 мин ∙ 7 = 280 мин = 4 ч 40 мин – за неделю;
4 ч 40 мин ∙ 4 = 4 ч ∙ 4 + 40 мин ∙ 4 = 16 ч + 160 мин = 16 ч + 2 ч 40 мин = 18 ч 40 мин – за месяц.
3) Просмотр телевизора или игра в компьютер:
Каждый день смотрели телевизор или играли в компьютер по 30 минут в день. Значит просмотр телевизора или игра в компьютер заняло 3 ч 30 мин за неделю, а за месяц – 14 часов.
30 мин ∙ 7 = 210 мин = 3 ч 30 мин – за неделю;
3 ч 30 мин ∙ 4 = 3 ч ∙ 4 + 30 мин ∙ 4 = 12 ч + 120 мин = 12 ч + 2 ч = 14 ч – за месяц.
4) Культурно-просветительный поход:
В 1 неделю посетили театр – 1 ч 30 мин;
Во 2 неделю посетили кинотеатр – 1 ч 15 мин;
В 3 неделю посетили Музей иллюзий – 3 часа;
В 4 неделю посетили Планетарий – 2 часа.
Значит, на культурный поход заняло 7 ч 45 мин за месяц.
1 ч 30 мин + 1 ч 15 мин + 3 ч + 2 ч = 7 ч 45 мин.
5) Общее время, затраченное на досуг:
28 ч + 18 ч 40 мин + 14 ч + 7 ч 45 мин = 68 ч 25 мин.
Делаем вывод.
Вывод: На весь досуг за месяц было потрачено 68 ч 25 мин.
Проект 4.
Тема Тема «Денежные расходы на экскурсию, посещение театра или музея, на поездку за город или в город.».
Ответ:1) К примеру возьмём поездку в Московский планетарий;
2) Задача проекта: рассчитать стоимость поездки в Московский планетарий из Московской области (из расчета на одного человека);
3) Срок выполнения работы: 1 неделя;
4) Данный проект лучше выполнять в группе.
План работы
1) Распределить работу между членами группы;
2) Собрать нужную информацию;
– о местонахождении Московского планетария и стоимости проезда;
– о времени работы планетария и стоимости билета;
– о кафе рядом с Московским планетарием;
– оформление проекта и вывода.
3) Оформить проект.
4) Сделать вывод.
1) Поездка в Московский планетарий;
2) Задача проекта: рассчитать стоимость поездки в Московский планетарий из Московской области (из расчета на одного человека);
3) Срок выполнения работы: 1 неделя;
4) Данный проект лучше выполнять в группе.
Составим план.
1) Распределить работу между членами группы;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
Распределим работу между членами группы.
1) Сбор информации о местонахождении Московского планетария и стоимости проезда;
2) Сбор информации о времени работы планетария и стоимости билета;
3) Сбор информации о кафе рядом с Московским планетарием;
4) Оформление проекта и вывода.
Соберем нужную информацию и оформим её в таблицу.
1) Чтобы нам доехать до планетария нужно вначале ехать на электричке, а потом на метро.
2) Планетарий работает с 10:00 до 22:00.
Стоимость билета на мероприятие «Город Солнца» - 650 рублей.
Оформим проект в виде таблицы.
-(2024).jpg)
Рассчитаем
Посчитаем сколько тратится времени на выполнение каждой работы за неделю.
1) Билет на электричку: 170 руб. ∙ 2 = (100 + 70) ∙ 2 = 200 + 140 = 340 руб.
2) Билет в метро: 60 руб. ∙ 2 = 120 руб.
3) Общее сумма денег, потраченная на поездку в Московский планетарий:
340 руб. + 120 руб.+ 650 руб. + 500 руб. = 1610 руб.
Делаем вывод.
Вывод: для поездки в Московский планетарий каждый ученик должен потратить около 1610 рублей.
Проект 5.
Тема «Расчёт количества и стоимости покупки обоев для оклейки одной комнаты в своей квартире».
Ответ:1) Задача проекта: рассчитать количество и стоимость обоев для оклейки стен в комнате;
2) Срок выполнения работы: 2 недели.
План работы
1) Составить список нужной информации;
– о стоимости обоев;
– о ширине и длине рулона обоев;
– о параметрах комнаты;
– о параметрах двери и окна.
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
1) Задача проекта: рассчитать количество и стоимость обоев для оклейки стен в комнате;
2) Срок выполнения работы: 2 недели.
Составим план.
1) Составить список нужной информации;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
Составим список нужной информации:
Нужно собрать информацию:
– о стоимости обоев;
– о ширине и длине рулона обоев;
– о параметрах комнаты;
– о параметрах двери и окна.
Соберем информацию.
1) Обои выбрали по стоимости 1600 рублей за рулон;
2) Измерим ширину и длину рулона:
Ширина – 1 м ; Длина – 10 м;
3) Измерим длину, ширину и высоту комнаты:
Длина – 3 м; Ширина – 4 м; Высота – 3 м.
4) Измерим параметры двери и окна:
Окно: 1 м 50 см на 1 м 50 см;
Дверь: 2 м на 1 м.
Выполним вычисления и оформим проект.
Вычислим периметр комнаты, окна и двери:
Чтобы найти периметр нужно сумму длины и ширины умножить на 2.
1) (3 + 4) ∙ 2 = 7 ∙ 2 = 14 (м) – периметр комнаты;
2) (1 м 50 см + 1 м 50 см) ∙ 2 = 3 м ∙ 2 = 6 м – периметр окна;
3) (2 + 1) ∙ 2 = 3 ∙ 2 = 6 м – периметр двери.
Узнаем сколько понадобится обоев:
Так как периметр комнаты 14 м, значит нужно 14 полос обоев по 3 м в высоту (так как высота комнаты 3 м).
1) 14 ∙ 3 = (10 + 4) ∙ 3 = 40 + 12 = 52 (м) – нужно обоев без учета окна и двери.
2) 52 – 6 – 6 = 52 – 12 = 40 (м) – нужно обоев с учетом окна и двери.
Вычислим сколько понадобится рулонов обоев:
Чтобы узнать сколько можно вырезать полос из 1 рулона обоев, нужно длину обоев разделить на высоту комнаты:
10 : 3 = 3 (ост. 1)
Из 1 рулона выходит 3 полосы по 3 метра и остаток 1 м.
Чтобы узнать сколько на комнату понадобится полос обоев, нужно количество обоев разделить на количество полос в одном рулоне:
40 : 3 = 13 (ост. 1)
Значит понадобится 14 полос обоев.
Чтобы узнать сколько рулонов обоев понадобится нужно количество полос, которые понадобятся на поклейку комнаты, разделить на количество полос в одном рулоне:
14 : 3 = 4 (ост. 2)
Значит понадобится 5 рулонов обоев.
Вычислим общую стоимость обоев:
1600 ∙ 5 = 8000 (руб.), так как:
16 ∙ 5 = (10 + 6) ∙ 5 = 50 + 30 = 80
Делаем вывод.
Вывод: Чтобы оклеить комнату понадобится 5 рулонов обоев;
Стоимость оклейки обоев в комнату стоит 8000 рублей.
Проект 6.
Тема «Расчёт площади, занимаемой спортивными снарядами в школьном спортзале, и площади зала, которая приходится на одного человека во время урока физкультуры.»
Ответ:1) Задача проекта: рассчитать площади, занимаемой спортивными снарядами в школьном спортзале, и площади зала, которая приходится на одного человека во время урока физкультуры;
2) Срок выполнения работы: 3 дня.
План работы
1) Составить список нужной информации;
– о параметрах спортивного зала;
– о параметрах места под спортивные снаряды;
– количество учащихся в классе.
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
1) Задача проекта: рассчитать площади, занимаемой спортивными снарядами в школьном спортзале, и площади зала, которая приходится на одного человека во время урока физкультуры;
2) Срок выполнения работы: 3 дня.
Составим план.
1) Составить список нужной информации;
2) Собрать нужную информацию;
3) Оформить проект.
4) Сделать вывод.
Составим список нужной информации:
Нужно собрать информацию:
– о параметрах спортивного зала;
– о параметрах места под спортивные снаряды;
– количество учащихся в классе.
Соберем информацию.
1) Узнаем параметры спортивного зала (можно спросить у учителя):
Длина – 18 м; ширина – 9 м.
2) Узнаем параметры, под спортивные снаряды (можно спросить у учителя):
Длина – 6 м, ширина – 3 м.
3) Количество учеников в классе: 20 учеников.
Выполним вычисления и оформим проект.
1) Вычислим площадь спортивного зала:
18 ∙ 9 = 162 (м2), так как:
18 ∙ 9 = (10 + 8) ∙ 9 = 90 + 72 = 162
2) Вычислим площадь, под спортивные снаряды:
6 ∙ 3 = 18 (м2)
3) Узнаем площадь зала, которая приходится для всего класса:
162 – 18 = 144 (м2)
4) Узнаем площадь зала, которая приходится на одного человека:
144 : 20 ≈ 140 : 20 = 14 дес. : 2 дес. = 14 : 2 = 7 (м2)
Так как мы ещё не знаем, как 144 разделить на 20, то разделим 140 на 20 и узнаем приблизительное значение.
Данный знак ≈ обозначает приблизительно равно.
Делаем вывод.
Вывод: Площадь, занимаемая спортивными снарядами в школьном спортзале равна 18 м2;
Площади зала, которая приходится на одного человека во время урока физкультуры примерно 7 м2.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.