Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 32

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Выполни деление с остатком и проверь:
Ответ:
Выполнять проверку деления с остатком.
Вспомни, как выполнить проверку деления с остатком.
Рассуждаем.
Найдём частное методом подбора.
50 : 15 = ?
Надо 50 разделить на 15.
Пробуем, например, в частном 2.
Проверим: 15 ∙ 2 = 30.
Найдём остаток и сравним его с делителем:
50 - 30 = 20, 20 > 15, значит, 2 мало.
Пробуем в частном 3.
Проверим: 15 ∙ 3 = 45;
50 - 45 = 5, 5 < 15, значит, частное 3, а остаток 5.
Ответ: 50 : 15 = 3 (ост. 5)
18 : 27 = ?
Надо 18 разделить на 27.
Так как 18 < 27, то целых частей нет.
Ответ: 18 : 27 = 0 (ост. 18)
89 : 22 = ?
Надо 89 разделить на 22.
Пробуем, например, в частном 3.
Проверим: 22 ∙ 3 = 66.
Найдём остаток и сравним его с делителем:
89 - 66 = 23, 23 > 22, значит, 3 мало.
Пробуем в частном 3.
Проверим: 22 ∙ 4 = 88;
89 - 88 = 1, 1 < 22, значит, частное 4, а остаток 1.
Ответ: 89 : 22 = 4 (ост. 1)
75 : 18 = ?
Надо 75 разделить на 18.
Пробуем, например, в частном 3.
Проверим: 18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 24 = 54.
Найдём остаток и сравним его с делителем:
75 - 54 = 21, 21 > 18, значит, 3 мало.
Пробуем в частном 4.
Проверим: 18 ∙ 4 = 72;
75 - 72 = 3, 3 < 18, значит, частное 4, а остаток 3.
Ответ: 75 : 18 = 4 (ост. 3)
100 : 30 = ?
Надо 100 разделить на 30.
Пробуем, например, в частном 2.
Проверим: 30 ∙ 2 = 60.
Найдём остаток и сравним его с делителем:
100 - 60 = 40, 40 > 30, значит, 2 мало.
Пробуем в частном 3.
Проверим: 30 ∙ 3 = 90;
100 - 90 = 10, 10 < 30, значит, частное 3, а остаток 10.
Ответ: 100 : 30 = 3 (ост. 10)
57 : 42 = ?
Надо 57 разделить на 42.
Пробуем, например, в частном 1.
Проверим: 42 ∙ 1 = 42.
Найдём остаток и сравним его с делителем:
57 - 42 = 15, 15 < 42, значит, частное 1, а остаток 15.
Ответ: 57 : 42 = 1 (ост. 5)
28 : 17 = ?
Надо 28 разделить на 17.
Пробуем, например, в частном 1.
Проверим: 17 ∙ 1 = 17.
Найдём остаток и сравним его с делителем:
28 - 17 = 11, 11 < 17, значит, частное 1, а остаток 11.
Ответ: 28 : 17 = 1 (ост. 11)
76 : 20 = ?
Надо 76 разделить на 20.
Пробуем, например, в частном 2.
Проверим: 20 ∙ 2 = 40.
Найдём остаток и сравним его с делителем:
76 - 40 = 36, 36 > 20, значит, 2 мало.
Пробуем в частном 3.
Проверим: 20 ∙ 3 = 60;
76 - 60 = 16, 16 < 20, значит, частное 3, а остаток 16.
Ответ: 76 : 20 = 3 (ост. 16)
25 : 26 = ?
Надо 25 разделить на 26.
Так как 25 < 26, то целых частей нет.
Ответ: 25 : 26 = 0 (ост. 25)
9 : 13 = 0 (ост. 9)
Надо 9 разделить на 13.
Так как 9 < 13, то целых частей нет.
Ответ: 9 : 13 = 0 (ост. 9)
Выполняем проверку и оформляем задание в тетрадь.
50 : 15 = 3 (ост. 5)
Проверка:
5 < 15
15 ∙ 3 + 5 = 50
18 : 27 = 0 (ост. 18)
Проверка:
18 < 27
27 ∙ 0 + 18 = 18
89 : 22 = 4 (ост. 1)
Проверка:
1 < 22
22 ∙ 4 + 1 = 89
75 : 18 = 4 (ост. 3)
Проверка:
3 < 18
18 ∙ 4 + 3 = 75
100 : 30 = 3 (ост. 10)
Проверка:
10 < 30
30 ∙ 3 + 10 = 100
57 : 42 = 1 (ост. 15)
Проверка:
15 < 42
42 ∙ 1 + 15 = 57
28 : 17 = 1 (ост. 11)
Проверка:
11 < 17
1 ∙ 17 + 11 = 28
76 : 20 = 3 (ост. 16)
Проверка:
16 < 20
3 ∙ 20 + 16 = 76
25 : 26 = 0 (ост. 25)
Проверка:
25 < 26
26 ∙ 0 + 25 = 25
9 : 13 = 0 (ост. 9)
Проверка:
9 < 13
13 ∙ 0 + 9 = 9
Номер 2.
Ответ:
а : b, значит, значение a нужно разделить на b.
Рассуждаем.
Представим данные выражения в виде уравнений.
72 : 2 = х
72 : 2 = (60 + 12) : 2 = 30 + 6 = 36
х = 36
72 : 3 = х
72 : 3 = (60 + 12) : 3 = 20 + 4 = 24
х = 24
х : 4 = 18
х = 18 ∙ 4
18 ∙ 4 = (10 + 8) ∙ 4 = 40 + 32 = 72
х = 72
х : 6 = 12
х = 12 ∙ 6
12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72
х = 72
х : 8 = 9
х = 9 ∙ 8
х = 72
72 : х = 72
х = 72 : 72
х = 1
72 : х = 1
х = 72 : 1
х = 72
Оформляем задание в тетрадь.
Подставим полученные значения в таблицу.
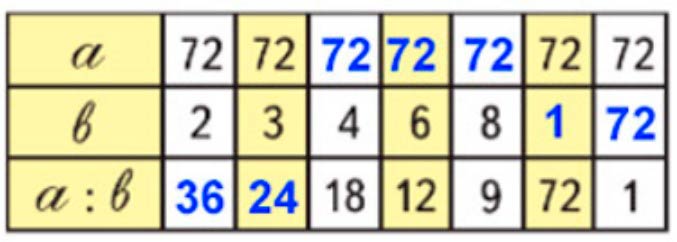
Номер 3.
Половину пути от дома до школы мальчик прошел за 15 мин, а на остальной путь он затратил на 6 мин больше. Сколько времени он затратил на весь путь до школы?
Ответ:
1-й способ решения:
1) 15 + 6 = 21 (мин) – затратил на остальной путь.
2) 15 + 21 = 36 (мин) – всё время пути.
Ответ: 36 минут времени занял весь путь мальчика до школы.
2-й способ решения:
(15 + 6) + 15 = 21 + 15 = 36 (мин.) – весь путь.
Ответ: 36 минут времени занял весь путь мальчика до школы.
«на 6 минут больше» – значит столько же, но ещё 6 минут.
Оформляем условие в виде краткой записи или схематического рисунка.
Краткая запись.
.jpg)
Схематический рисунок.
.jpg)
Рассуждаем.
Вторая часть пути на 6 минут больше, чем первая половина. Значит, к первой части пути нужно прибавить 6.
15 + 6 = 21 (мин.) – 2 часть пути.
Продолжаем рассуждение.
Весь путь складывается из первой и второй части пути. Значит, чтобы найти сколько времени мальчик затратил на весь путь, нужно сложить время первого пути и время второго пути.
15 + 21 = 36 (мин.) – потратил на весь путь.
Записываем ответ.
Ответ: 36 минут.
Решение выражением:
(15 + 6) + 15 = 36 (мин.) – весь путь, где 15 + 6 – время, затраченное на вторую часть пути.
Номер 4.
Начерти квадрат, площадь которого равна 4 см2. Раскрась его четвертую часть. Покажи, как это можно сделать по-разному. Сколько квадратных сантиметров раскрашено? Чему равна площадь нераскрашенной части?
Ответ:
1 см2 – раскрашен. S нераскрашенной части 3 см2. Ответ: площадь закрашенной части 1 см2, площадь незакрашенной части 3 см2.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
3) Чтобы найти площадь квадрата нужно его сторону умножить два раза.
Рассуждаем.
Найдем сторону квадрата.
Чтобы найти площадь квадрата нужно его сторону умножить два раза и это произведение равно 4 см2.
Значит, нужно подобрать такое число, которое при умножении само себя в произведении равно 4. Это число 2.
2 ∙ 2 = 4
Значит сторона квадрата равна 2 см.
Продолжаем рассуждение.
Найдем площадь раскрашенной и нераскрашенной части.
Раскрашенная часть квадрата – это одна четвертая часть. Значит, квадрат нужно разделить на 4 части и взять одну такую часть.
4 см2 : 4 = 1 см2 – площадь раскрашенной части.
Весь квадрат состоит из раскрашенной части и нераскрашенной части. Значит, чтобы найти площадь нераскрашенной части, нужно из общей площади квадрата вычесть площадь раскрашенной части.
4 см2 – 1 см2 = 3 см2 – площадь нераскрашенной части.
Выполним задание.
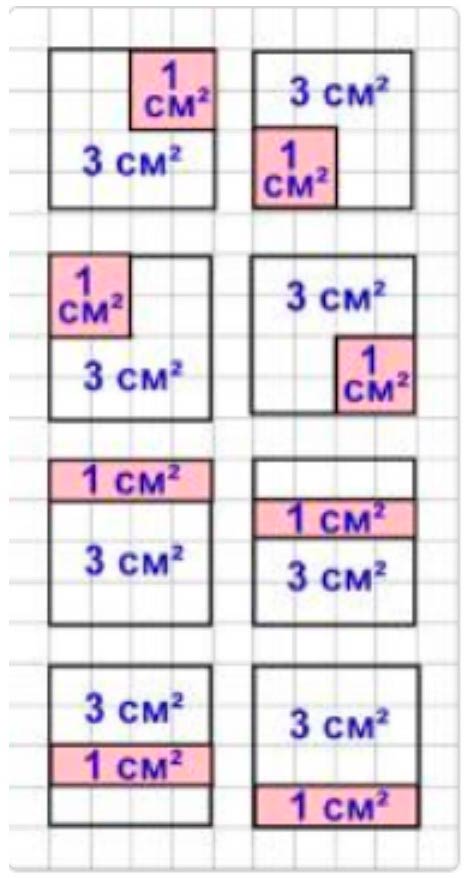
1 см2 – площадь раскрашенной части.
3 см2 – площадь нераскрашенной части.
Номер 5.
Ответ:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним деление методом подбора.
45 : 15 = ?
Надо 45 разделить на 15.
Пробуем, например, в частном 2.
Проверяем: 15 ∙ 2 = 30, 30 < 45, число 2 не подходит.
Пробуем в частном 3.
Проверяем: 15 ∙ 3 = 45, 45 = 45, значит 45 : 15 = 3.
Пробуем в частном 2 и проверяем: 29 2 58,
58 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 3 87,
87 87, значит, 87 29 3.
Пробуем в частном 2 и проверяем: 29 2 58,
58 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 3 87,
87 87, значит, 87 29 3.
Пробуем в частном 2 и проверяем: 29 2 58,
58 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 3 87,
87 87, значит, 87 29 3.
Пробуем в частном 2 и проверяем: 29 2 58,
58 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 3 87,
87 87, значит, 87 29 3.
Пробуем в частном 2 и проверяем: 29 2 58,
58 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 3 87,
87 87, значит, 87 29 3.
99 : 33 = ?
Надо 99 разделить на 33.
Пробуем, например, в частном 2.
Проверяем: 33 ∙ 2 = 66, 66 < 99, число 2 не подходит.
Пробуем в частном 3.
Проверяем: 33 ∙ 3 = 99, 99 = 99, значит 99 : 33 = 3.
80 : 16 = ?
Надо 80 разделить на 16.
Пробуем, например, в частном 4.
Проверяем: 16 ∙ 4 = 64, 64 < 80, число 4 не подходит.
Пробуем в частном 5.
Проверяем: 16 ∙ 5 = 80, 80 = 80, значит 80 : 16 = 5.
Выполним вычисления по действиям.
78 : 6 ∙ 3 = 39
1) 78 : 6 = (60 + 18) : 6 = 60 : 6 + 18 : 6 = 10 + 3 = 13
2) 13 ∙ 3 = (10 + 3) ∙ 3 = 10 ∙ 3 + 3 ∙ 3 = 30 + 9 = 39
51 : 3 ∙ 4 = 68
1) 51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
2) 17 ∙ 4 = (10 + 7) ∙ 4 = 10 ∙ 4 + 7 ∙ 4 = 40 + 28 = 68
84 : 4 ∙ 3 = 63
1) 84 : 4 = 21
2) 21 ∙ 3 = (20 + 1) ∙ 3 = 20 ∙ 3 + 1 ∙ 3 = 60 + 3 = 63
100 − 2 ∙ 18 = 64
1) 2 ∙ 18 = 2 ∙ (10 + 8) = 2 ∙ 10 + 2 ∙ 8 = 20 + 16 = 36
2) 100 − 36 = 64
100 − 3 ∙ 18 = 46
1) 3 ∙ 18 = 3 ∙ (10 + 8) = 3 ∙ 10 + 3 ∙ 8 = 30 + 24 = 54
2) 100 − 54 = 46
100 − 4 ∙ 18 = 28
1) 4 ∙ 18 = 4 ∙ (10 + 8) = 4 ∙ 10 + 4 ∙ 8 = 40 + 32 = 72
2) 100 − 72 = 28
(34 + 36) : 10 = 7
1) 34 + 3 6 = 70
2) 70 : 10 = 7
(75 − 33) : 3 = 14
1) 75 − 33 = 42
2) 42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14
(82 − 16) : 33 = 2
1) 82 − 16 = 66
2) 66 : 33 = 2
Оформляем задание в тетрадь.
45 : 15 = 3, так как 15 ∙ 3 = 45
99 : 33 = 3, так как 33 ∙ 3 = 99
80 : 16 = 5, так как 16 ∙ 5 = 80
78 : 6 ∙ 3 = 13 ∙ 3 = 39
51 : 3 ∙ 4 = 17 ∙ 4 = 68
84 : 4 ∙ 3 = 21 ∙ 3 = 63
100 − 2 ∙ 18 = 100 − 36 = 64
100 − 3 ∙ 18 = 100 − 54 = 46
100 − 4 ∙ 18 = 100 − 72 = 28
(34 + 36) : 10 = 70 : 10 = 7
(75 − 33) : 3 = 42 : 3 = 14
(82 − 16) : 33 = 66 : 33 = 2
1) 82 − 16 = 66
2) 66 : 33 = 2
Номер 6.
Измерь стороны многоугольников в миллиметрах и найди периметр каждого из них.

Р1 = 24 ∙ 4 = 96 мм Р2 = 33 ∙ 3 = 99 мм Р3 = 15 ∙ 6 = 90 мм Ответ: периметр первого многоугольника составляет 96 мм, периметр второго многоугольника составляет 99 мм, периметр третьего многоугольника составляет 90 мм
Периметр фигуры – суммы длин всех ее сторон.
Для измерения сторон используй линейку.
Измерим стороны фигур.
Измерим с помощью линейки все стороны каждой фигуры.
Квадрат: все его стороны равны – 2 см 4 мм = 24 мм
Треугольник: все его стороны равны – 3 см 3 мм = 33 мм
Шестиугольник: все его стороны равны – 1 см 5 мм = 15 мм
Вычислим периметры.
Чтобы найти периметр нужно сложить все стороны данной фигуры:
Так как у квадрата 4 стороны, и они все равны, то:
1) 24 мм ∙ 4 = 96 мм = 9 см 6 мм – периметр квадрата.
Так как у данного треугольника 3 стороны, и они все равны, то:
2) 33 мм ∙ 3 = 99 мм = 9 см 9 мм – периметр треугольника.
Так как у данного шестиугольника 6 сторон, и они все равны, то:
3) 15 мм ∙ 6 = 90 мм = 9 см – периметр шестиугольника.
Оформляем задание в тетрадь.
1) 24 мм ∙ 4 = 96 мм – периметр квадрата.
2) 33 мм ∙ 3 = 99 мм – периметр треугольника.
3) 15 мм ∙ 6 = 90 мм – периметр шестиугольника.
Номер 7.
Используя только цифры 1, 2, 3, 4, 5, 6, 7 и не повторяя ни одну из них, составь такие 4 числа, чтобы при их сложении получилось 100.
Ответ:2 + 17 + 35 + 46 = 100 5 + 12 + 36 + 47 = 100 6 + 15 + 37 + 42 = 100 6 + 15 + 32 + 47 = 100 7 + 14 + 23 + 56 = 100 7 + 16 + 35 + 42 = 100
Внимательно рассмотри цифры и составь такие числа, чтобы их сумма была равна 100.
Рассуждаем.
Посмотри внимательно какие цифры в сумме дают число, оканчивающееся на 0. Комбинируй их. Цифры можно переставлять местами.
Выполняем задание.
Выбери один из возможных вариантов или запиши свой:
2 + 17 + 35 + 46 = 100
2 + 15 + 36 + 47 = 100
3 + 24 + 56 + 17 = 100
4 + 16 + 9 + 71 = 100
5 + 12 + 36 + 47 = 100
5 + 36 + 17 + 42 = 100
6 + 15 + 37 + 42 = 100
7 + 13 + 26 + 54 = 100
8 + 12 + 74 + 6 = 100
9 + 1 + 63 + 27 = 100
Задание внизу страницы
Выполни проверку деления с остатком.
Ответ:65 : 20 = 3(ост.5) 39 : 12 = 3(ост.3) Проверка Проверка 5 < 20 3 < 12 20 ∙ 3 + 5 = 65 12 ∙ 3 + 3 = 39
1) Повтори, как выполняется деление с остатком.
2) Повтори случаи вне табличного деления.
Рассуждаем.
Чтобы сделать проверку нужно:
1) убедиться, что остаток меньше делителя;
2) частное умножить на делитель и прибавить к произведению остаток, должно получиться делимое.
Если хотя бы один пункт не выполняется, то деление выполнено не верно.
Оформляем задание в тетрадь.
65 : 20 = 3 (ост. 5)
1) 20 ∙ 3 = 60 – неполное делимое
2) 60 + 5 = 65 – делимое
65 = 65
3) 5 < 20 – остаток должен быть меньше делителя.
39 : 12 = 3 (ост. 3)
1) 12 ∙ 3 = 36 – неполное делимое
2) 36 + 3 = 39 – делимое
39 = 39
3) 3 < 12 – остаток должен быть меньше делителя.
Номер 9.
С трех серых овец настригли в год 18 кг шерсти, со всех поровну. Сколько шерсти можно настричь с пяти черных овец, если с каждой овцы получили на 1 кг меньше?
Ответ:
1) 18 : 3 = 6 (кг) - шерсти собирают с каждой серой овцы за год
2) 6 - 1 = 5 (кг) - шерсти будут состригать с каждой чёрной овцы за год
3) 5 ∙ 5 = 25 (кг) - шерсти всего с чёрных овец
Ответ: 25 кг шерсти всего можно настричь с пяти чёрных овец.
«на 1 кг меньше» - это столько же, но минус 1 кг.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
С каждой серой овцы настригли одинаковое количество шерсти. Значит, чтобы найти сколько шерсти настригли с одной серой овцы, нужно общее количество шерсти разделить на количество овец.
18 : 3 = 6 (кг) – шерсти настригли с одной серой овцы.
Продолжаем рассуждение.
Мы знаем, что с 1 чёрной овцы настригают на 1 кг меньше шерсти, чем с 1 серой овцы. Значит, чтобы узнать сколько с одной черной овцы настригли шерсти, нужно из количества шерсти с одной серой овцы вычесть 1 кг.
6 – 1 = 5 (кг) – шерсти собрали с одной черной овцы.
Продолжаем рассуждение.
Мы узнали, что с одной черной овцы настригают 5 кг шерсти. Чтобы узнать, сколько всего настригли шерсти с чёрных овец, нужно количество шерсти с одной овцы умножить на количество овец.
5 ∙ 5 = 25 (кг) – шерсти можно настричь с пяти черных овец.
Записываем ответ.
Ответ: 25 кг шерсти можно настричь с пяти черных овец.
Номер 10.
Выполни деление с остатком.
Ответ:8 : 7 = 1 (ост. 1) 50 : 9 = 5 (ост. 5)
8 : 6 = 1 (ост. 2) 40 : 9 = 4 (ост. 4)
5 : 8 = 0 (ост. 5) 30 : 9 = 3 (ост. 3)
61 : 7 = 8 (ост. 5) 48 : 20 = 2 (ост. 8)
84 : 9 = 9 (ост. 3) 56 : 10 = 5 (ост. 6)
70 : 8 = 8 (ост. 6) 32 : 20 = 1 (ост. 12)
14 : 30 = 0 (ост. 14)
8 : 10 = 0 (ост. 8)
9 : 12 = 0 (ост. 9)
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
8 : 7 = 1 (ост. 1)
8 не делится на 7 без остатка. Вспомним, какое самое большое число до 8 делится на 7 без остатка. Это 7.
Найдём частное: 7 : 7 = 1.
Найдём остаток: 8 – 7 = 1.
8 : 6 = 1 (ост. 2)
8 не делится на 6 без остатка. Вспомним, какое самое большое число до 8 делится на 6 без остатка. Это 6.
Найдём частное: 6 : 6 = 1.
Найдём остаток: 8 – 6 = 2.
5 : 8 = 0 (ост. 5)
Надо 5 разделить на 8.
Так как 5 < 8, то целых частей нет, а остаток 5.
50 : 9 = 5 (ост. 5)
50 не делится на 9 без остатка. Вспомним, какое самое большое число до 50 делится на 9 без остатка. Это 45.
Найдём частное: 45 : 9 = 5.
Найдём остаток: 50 – 45 = 5.
40 : 9 = 4 (ост. 4)
40 не делится на 9 без остатка. Вспомним, какое самое большое число до 40 делится на 9 без остатка. Это 36.
Найдём частное: 36 : 9 = 4.
Найдём остаток: 40 – 36 = 4.
30 : 9 = 3 (ост. 3)
30 не делится на 9 без остатка. Вспомним, какое самое большое число до 30 делится на 9 без остатка. Это 27.
Найдём частное: 27 : 9 = 3.
Найдём остаток: 30 – 27 = 3.
61 : 7 = 8 (ост. 5)
61 не делится на 7 без остатка. Вспомним, какое самое большое число до 61 делится на 7 без остатка. Это 56.
Найдём частное: 56 : 7 = 8.
Найдём остаток: 61 – 56 = 5.
84 : 9 = 9 (ост. 3)
84 не делится на 9 без остатка. Вспомним, какое самое большое число до 84 делится на 9 без остатка. Это 81.
Найдём частное: 81 : 9 = 9.
Найдём остаток: 84 – 81 = 3.
70 : 8 = 8 (ост. 6)
70 не делится на 8 без остатка. Вспомним, какое самое большое число до 70 делится на 8 без остатка. Это 64.
Найдём частное: 64 : 8 = 8.
Найдём остаток: 70 – 64 = 6.
48 : 20 = 2 (ост. 8)
Надо 48 разделить на 20.
Пробуем в частном 2.
Проверим: 20 ∙ 2 = 2 дес. ∙ 2 = 4 дес. = 40.
Найдём остаток и сравним его с делителем: 48 – 40 = 8, 8 < 20, значит, частное 2, а остаток 8.
56 : 10 = 5 (ост. 6)
Надо 56 разделить на 10.
Пробуем в частном 5.
Проверим: 10 ∙ 5 = 50.
Найдем остаток и сравним его с делителем: 56 – 50 = 6, 6 < 10, значит, частное 5, а остаток 6.
32 : 20 = 1 (ост. 12)
Надо 32 разделить на 20.
Пробуем в частном 1. Проверим: 20 ∙ 1 = 20.
Найдём остаток и сравним его с делителем: 32 – 20 = 12, 12 < 20, значит, частное 1, а остаток 12.
14 : 30 = 0 (ост. 14)
Надо 14 разделить на 30.
Так как 14 < 30, то целых частей нет, а остаток 14.
Надо 8 разделить на 10.
Так как 8 < 10, то целых частей нет, а остаток 8.
9 : 12 = 0 (ост. 9)
Надо 9 разделить на 12.
Так как 9 < 12, то целых частей нет, а остаток 9.
Оформляем задание в тетрадь.
8 : 7 = 1 (ост. 1)
8 : 6 = 1 (ост. 2)
5 : 8 = 0 (ост. 5)
50 : 9 = 5 (ост. 5)
40 : 9 = 4 (ост. 4)
30 : 9 = 3 (ост. 3)
61 : 7 = 8 (ост. 5)
84 : 9 = 9 (ост. 3)
70 : 8 = 8 (ост. 6)
48 : 20 = 2 (ост. 8)
56 : 10 = 5 (ост. 6)
32 : 20 = 1 (ост. 12)
14 : 30 = 0 (ост. 14)
8 : 10 = 0 (ост. 8)
9 : 12 = 0 (ост. 9)
Номер 11.
1) Назови по 3 числа, при делении которых на 10 в остатке может получиться 2; 4; 0. 2) Может ли при делении на 6 получиться в остатке 9? при делении на 12 получиться в остатке 11? 13? 10? 3) Какие остатки могут получиться при делении на 5? на 8? на 3? на 12?
Ответ:1) 12, 22, 32; 14, 24, 34; 10, 20, 30. 2) При делении на 6 не может быть остаток 9, так как остаток всегда меньше делителя. При делении на 12 может быть остаток 11 и 9, 10, но не 13. 3) При делении на 5 остатки: 1, 2, 3, 4; на 8 – 1, 2, 3, 4, 5, 6, 7; на 3 – 1, 2; на 12 – 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
1) Повтори, как выполняется деление с остатком.
2) Вспомни, что остаток всегда меньше делителя.
Рассуждаем.
Вспомним число, которое делится на 10 без остатка, оканчивающееся на 0.
Чтобы при делении на 10 остаток был равен 2, то делимое должно оканчиваться на 2.12 : 10 = 1 (ост. 2)
22 : 10 = 2 (ост. 2)
32 : 10 = 3 (ост. 2)
Чтобы при делении на 10 остаток был равен 4, то делимое должно оканчиваться на 4.
14 : 10 = 1 (ост. 4)
24 : 10 = 2 (ост. 4)
34 : 10 = 2 (ост. 4)
Чтобы при делении на 10 остаток был равен 0, то делимое должно оканчиваться на 0.
10 : 10 = 1 (ост. 0)
20 : 10 = 3 (ост. 0)
30 : 10 = 5 (ост. 0)
Продолжаем рассуждения.
Помним, что остаток должен быть меньше делителя.
Остаток при делении на 6 может быть – 0, 1, 2, 3, 4, 5.
Поэтому, при делении на 6 не может получиться остаток 9.
Остаток при делении на 12 может быть – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
Поэтому, при делении на 12 может получиться остаток 10 и 11, но не 13.
Продолжаем рассуждения.
Помним, что остатки при делении должны быть меньше делителя.
Остаток при делении на 5 может быть – 0, 1, 2, 3, 4.
Остаток при делении на 8 может быть – 0, 1, 2, 3, 4, 5, 6, 7.
Остаток при делении на 3 может быть – 0, 1, 2.
Остаток при делении на 12 может быть – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
Оформляем задание в тетрадь.
1) 12, 22, 32; 14, 24, 34; 10, 20, 30.
2) При делении на 6 остаток 9 получится не может, так как 9 > 6.При делении на 12 могут получиться остатки 10 и 11, так как 10 < 12 и 11 < 12. Но не может быть остатка 13, так как 13 > 12. 3) При делении на 5 остатки – 0, 1, 2, 3, 4.
На 8 – 0, 1, 2, 3, 4, 5, 6, 7.
На 3 – 0, 1, 2.
На 12 – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
Номер 12.
1) Узнай, во сколько раз разность чисел 56 и 42 меньше их суммы. 2) Узнай, на сколько разность чисел 56 и 42 меньше их суммы.
Ответ:1) (56 + 42) : (56 – 42) = 7 В 7 раз сумма чисел 56 и 42 больше их разности. 1) (56 + 42) – (56 – 42) = 84 На 84 сумма чисел 56 и 42 больше их разности.
1) разность – это знак минус;
2) сумма – это знак плюс.
Рассуждаем.
Составим выражения.
56 + 42 – сумма чисел 56 и 48
56 – 42 – разность чисел 56 и 48
(56 + 42) : (56 – 42) – во сколько раз разность меньше суммы.
(56 + 42) – (56 – 42) – на сколько разность меньше суммы.
Вычисляем.
(56 + 42) : (56 – 42) = 7 – во столько раз разность меньше суммы.
1) 56 + 42 = 98
2) 56 – 42 = 14
3) 98 : 14 = 7
(56 + 42) – (56 – 42) = 84 – на столько разность меньше суммы.
1) 56 + 42 = 98
2) 56 – 42 = 14
3) 98 – 14 = 84
Оформляем задание в тетрадь.
(56 + 42) : (56 – 42) = 98 : 14 = 7
В 7 раз сумма чисел 56 и 42 больше их разности.
(56 + 42) – (56 – 42) = 98 – 14 = 84
На 84 сумма чисел 56 и 42 больше их разности.
Номер 13.
Для закладки сада заготовили ☐ яблонь. Сколько яблонь осталось посадить, если уже посажено 5 рядов, по 16 яблонь в каждом ряду? Дополни условие и реши задачу.
Ответ:
1) 16 ∙ 5 = 80 (яб.) - посадили
2) 100 - 80 = 20 (яб.) - осталось посадить
Ответ: 20 яблонь осталось всего.
Мы подставили число 96, ты можешь подставить свое число и решить задачу
Дополняем условие задачи.
Для закладки сада заготовили 100 яблонь. Сколько яблонь осталось посадить, если уже посажено 5 рядов, по 16 яблонь в каждом ряду?
Оформляем краткую запись.
.jpg)
Рассуждаем.
Посадили 5 рядов по 16 яблонь, значит в каждом ряду количество яблонь одинаково. Чтобы узнать, сколько всего яблонь посадили, нужно количество яблонь в 1 ряду умножить на количество рядов.
16 ∙ 5 = (10 + 6) ∙ 5 = 50 + 30 = 80 (яб.) – посадили.
Продолжаем рассуждение.
Общее количество яблонь складывается из яблонь, которые посадили и которые осталось посадить. Значит, чтобы узнать, сколько яблонь осталось посадить, нужно из общего количества яблонь вычесть количество, которое уже посадили.
100 – 80 = 20 (яб.) – осталось посадить.
Записываем ответ.
Ответ: 20 яблонь осталось посадить.
Номер 14.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
3) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Расставляем порядок действий и выполняем вычисления.
45 : 15 = ?
Пробуем в частном 3 и проверяем:
15 ∙ 3 = (10 + 5) ∙ 3 = 30 + 15 = 45,
45 = 45, значит,
45 : 15 = 3.
72 : 12 = ?
Пробуем в частном 6 и проверяем:
12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72,
72 = 72, значит,
72 : 12 = 6.
54 : 18 = 3
Пробуем в частном 3 и проверяем:
18 ∙ 3 = (10 + 8) ∙ 3 = 30 + 14 = 54,
54 = 54, значит,
54 : 18 = 3.
1 2
91 : 13 ∙ 4 = 28
1) 91 : 13 = 7
2) 7 ∙ 4 = 28
1 2
60 : 15 ∙ 9 = 36
1) 60 : 15 = 4
2) 4 ∙ 9 = 36
1 2
70 : 14 ∙ 8 = 40
1) 70 : 14 = 5
2) 5 ∙ 8 = 40
1 2
(32 − 16) ∙ 4 = 64
1) 32 – 16 = 16
2) 16 ∙ 4 = (10 + 6) ∙ 4 = 40 + 24 = 64
1 2
(46 – 21) ∙ 3 = 75
1) 46 – 21 = 25
2) 25 ∙ 3 = (20 + 5) ∙ 3 = 60 + 15 = 75
1 2
(30 – 18) ∙ 7 = 84
1) 30 – 18 = 12
2) 12 ∙ 7 = (10 + 2) ∙ 7 = 70 + 14 = 84
2 1
15 – 8 ∙ 0 = 15
1) 8 ∙ 0 = 0
2) 15 – 0 = 15
1 2
14 ∙ 1 – 14 = 0
1) 14 ∙ 1 = 14
2) 14 – 14 = 0
2 1
0 : (13 – 6) = 0
1) 13 – 6 = 7
2) 0 : 7 = 0
Оформляем задание в тетрадь.
45 : 15 = 3
72 : 12 = 6
54 : 18 = 3
1 2
91 : 13 ∙ 4 = 7 ∙ 4 = 28
1 2
60 : 15 ∙ 9 = 4 ∙ 9 = 36
1 2
70 : 14 ∙ 8 = 5 ∙ 8 = 40
1 2
(32 − 16) ∙ 4 = 16 ∙ 4 = 64
1 2
(46 – 21) ∙ 3 = 25 ∙ 3 = 75
1 2
(30 – 18) ∙ 7 = 12 ∙ 7 = 84
2 1
15 – 8 ∙ 0 = 15 – 0 = 15
1 2
14 ∙ 1 – 14 = 14 – 14 = 0
2 1
0 : (13 – 6) = 0 : 7 = 0
Задание на полях страницы
Продолжи ряд чисел:


1) Для того, чтобы продолжить ряд чисел, необходимо увидеть закономерность.
2) Повтори, какие могут быть остатки при делении.
Рассуждаем.
Число из первой колонки делят на 4 и остаток записывают в правую колонку.
Вычисляем.
8 : 4 = 2 (ост. 0)
5 : 4 = 1 (ост. 1)
6 : 4 = 1 (ост. 2)
7 : 4 = 1 (ост. 3)
10 : 4 = 2 (ост. 2)
14 : 4 = 3 (ост. 2)
15 : 4 = 3 (ост. 3)
20 : 4 = 5 (ост. 0)
19 : 4 = 4 (ост. 3)
17 : 4 = 4 (ост. 1)
Продолжим ряд.
Ответ: 0, 3, 1.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.