Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 30

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Сколько порций по 3 блина выйдет, если всего испекли 18 блинов? 19 блинов? 25 блинов?
Ответ:
1) 18 : 3 = 6 (п.) – по 3 блина. 2) 19 : 3 = 6 (ост. 1) – 6 порций и 1 блин останется. 3) 25 : 3 = 8 (ост. 1) – 8 порций и 1 блин останется. Ответ: могут выйти такие порции блинов , если было разное количество блинов: 6 порций по 3 блина; 6 порций и 1 блин останется; 8 порций и 1 блин останется.
Данная задача: вида «кол-во порций, блинов в 1 порции, всего блинов» характеризуется зависимостями между компонентами:
Кол-во порций · блинов в 1 порции = всего блинов.
Всего блинов : кол-во порций = блинов в 1 порции.
Всего блинов : блинов в 1 порции = кол-во порций.
Оформляем условие в виде таблицы.

Рассуждаем.
Количество блинов, в каждой порции одинаковое, значит, чтобы узнать, сколько получится порций, нужно общее количество блинов разделить на количество блинов в 1 порции.
1) 18 : 3 = 6 (п.) – из 18 блинов
Получится 6 полных порций.
2) 19 : 3 = 6 (ост. 1) – из 19 блинов
Получится 6 полных порций и 1 блин останется.
3) 25 : 3 = 8 (ост. 1) – из 20 блинов
Получится 18 полных порций и 1 блин останется
Записываем ответ.
Ответ: 6 порций; 6 порций и 1 останется; 8 порций и 1 останется.
Номер 2.
Какое самое большое число до 53 делится без остатка на 9? на 8? на 7?
Ответ:45 : 9 = 5 48 : 8 = 6 49 : 7 = 7
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Рассуждаем.
53 не делится на 9 без остатка. Вспомним, какое самое большое число до 53 делится на 9 без остатка. Это 45.
45 : 9 = 5
53 не делится на 8 без остатка. Вспомним, какое самое большое число до 53 делится на 8 без остатка. Это 48.
48 : 8 = 6
53 не делится на 7 без остатка. Вспомним, какое самое большое число до 53 делится на 7 без остатка. Это 49.
49 : 7 = 7
Оформляем задание в тетрадь.
Самое большое число до 53 делится без остатка.
На 9 – это число 45.
На 8 – это число 48.
На 7 – это число 49.
Номер 3.
Вычисли и проверь деление умножением.
Ответ:99 : 33 = 3 84 : 7 = 12
3 ∙ 33 = 99 12 ∙ 7 = 84
99 = 99 84 = 84
56 : 2 = 28 72 : 3 = 24
28 ∙ 2 = 56 24 ∙ 3 = 72
56 = 56 72 = 72
Вспомни зависимость между элементами и результатом действия умножения и деления.
Делимое : делитель = частное.
Делимое : частное = делитель.
Частное · делитель = делимое.
1множитель · 2множитель = произведение.
Произведение : 1множитель = 2множитель.
Произведение : 2 множитель = 1 множитель.
Вычисляем.
99 : 33 = 3
Пробуем в частном 2 и проверяем: 33 ∙ 2 = 66, 66 < 99, число 2 не подходит.
Пробуем в частном 3 и проверяем: 33 ∙ 3 = 99, 99 = 99, значит 99 : 33 = 3.
Ответ: 3.
Выполним деление с помощью правила деления суммы на число:
84 : 7 = (70 + 14) : 7 = 10 + 2 = 12
Представим число 84 в виде суммы 70 и 14, каждое слагаемое разделим на 7 и полученные результаты сложим.
56 : 2 = (40 + 16) : 2 = 20 + 8 = 28
Представим число 56 в виде суммы 40 и 16, каждое слагаемое разделим на 2 и полученные результаты сложим.
72 : 3 = (60 + 12) : 3 = 20 + 6 = 26
Представим число 72 в виде суммы 60 и 12, каждое слагаемое разделим на 3 и полученные результаты сложим.
Выполняем проверку.
Деление можно проверить умножением – частное умножить делитель.
99 : 33 = 3
Проверка:
33 ∙ 3 = (30 + 3) ∙ 3 = 90 + 9 = 99
99 = 99
Решение выполнено верно.
84 : 7 = 12
Проверка:
12 ∙ 7 = (10 + 2) ∙ 7 = 70 + 14 = 84
84 = 84
Решение выполнено верно.
56 : 2 = 28
Проверка:
28 ∙ 2 = (20 + 8) ∙ 2 = 40 + 16 = 56
56 = 56
Решение выполнено верно.
72 : 3 = 26
Проверка:
26 ∙ 3 = (20 + 6) ∙ 3 = 60 + 12 = 72
72 = 72
Решение выполнено верно.
Оформляем задание в тетрадь.
99 : 33 = 3
Проверка:
33 ∙ 3 = 99
99 = 99
84 : 7 = 12
Проверка:
12 ∙ 7 = 84
84 = 84
56 : 2 = 28
Проверка:
28 ∙ 2 = 56
56 = 56
72 : 3 = 26
Проверка:
26 ∙ 3 = 72
72 = 72
Номер 4.
В среду в библиотеке побывало 34 человека, в четверг – на 25 человек меньше, а в пятницу – в 3 раза больше, чем в четверг. Объясни, что означают выражения, и вычисли их значения:
Ответ:
34 - 25 = 9 (чел.) - было в четверг
(34 - 25) · 3 = 27 (чел.) - было в пятницу
Получается, выражения помогают определить:
34 - 25 - количество человек, которые были в библиотеке в четверг
(34 - 25) · 3 - количество человек, которые были в библиотеке в пятницу.
1) «на 25 меньше» – значит, из числа нужно вычесть 25.
2) «в 3 раза больше», значит, 3 раза по столько, т.е. умножить на 3.
Оформляем условие в виде краткой записи.
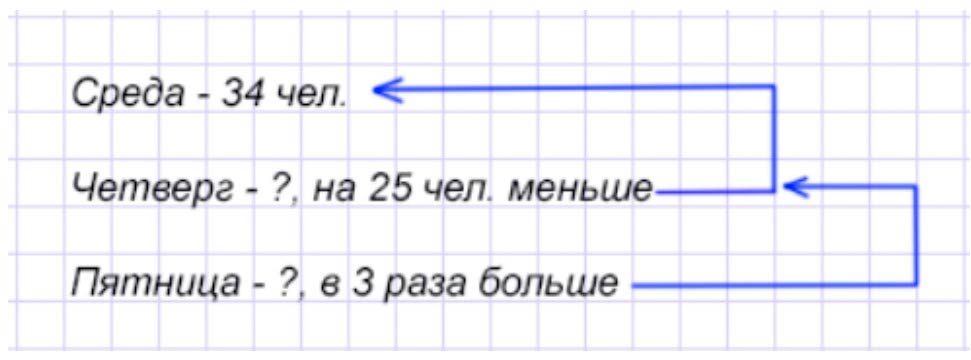
Рассуждаем.
Рассмотрим первое выражение.
Количество человек, которое было в среду уменьшили на 25. Также по условию, мы знаем, что в четверг было на 25 человек меньше, чем в среду. Значит, данным выражением мы найдём сколько человек было в библиотеке в четверг.
34 – 25 = 9 (ч.) – побывало в четверг.
Продолжаем рассуждение.
Рассмотрим второе выражение.
Количество человек, которое было в четверг умножили на 3, то есть увеличили в 3 раза. Также по условию, мы знаем, что в пятницу пришло в 3 раза больше человек, чем в четверг. Значит, данным выражением мы найдём сколько человек было в библиотеке в пятницу.
(34 − 25) ∙ 3 = 9 ∙ 3 = 27 (ч.) – пришло в пятницу.
Оформляем задание в тетрадь.
34 – 25 = 9 (чел.) – в четверг.
(34 − 25) ∙ 3 = 9 ∙ 3 = 27 (чел.) – в пятницу.
Номер 5.
Найди, не вычисляя, и выпиши парами выражения с одинаковыми значениями; проверь вычислением.
Ответ:
Вспомни о свойствах умножения:
а · b = b · a – переместительное свойство умножения – от перестановки мест слагаемых, произведение не изменяется.
Рассуждаем.
Выпишем парами выражения с одинаковыми значениями.
4 ∙ 7 = 7 ∙ 4 – применили переместительное свойство умножения
8 ∙ 5 = 5 ∙ 8 – применили переместительное свойство умножения
3 ∙ 9 = 9 ∙ 3 – применили переместительное свойство умножения
9 ∙ 8 = 8 ∙ 9 – применили переместительное свойство умножения
5 ∙ 7 + 5 = 5 ∙ 9 – 5, так как
5 ∙ 7 + 5 = 5 ∙ 8
5 ∙ 9 – 5 = 5 ∙ 8
8 ∙ 9 – 8 = 8 ∙ 7 + 8, так как
8 ∙ 9 – 8 = 8 ∙ 8
8 ∙ 7 + 8 = 8 ∙ 8
3 ∙ 10 – 3 = 3 ∙ 8 + 3, так как
3 ∙ 10 – 3 = 3 ∙ 9
3 ∙ 8 + 3 = 3 ∙ 9
7 ∙ 5 – 7 = 7 ∙ 3 + 7, так как
7 ∙ 5 – 7 = 7 ∙ 4
7 ∙ 3 + 7 = 7 ∙ 4
Делаем проверку.
4 ∙ 7 = 7 ∙ 4
Проверка:
4 ∙ 7 = 28
7 ∙ 4 = 28
28 = 28
8 ∙ 5 = 5 ∙ 8
Проверка:
8 ∙ 5 = 40
5 ∙ 8 = 40
40 = 40
3 ∙ 9 = 9 ∙ 3
Проверка:
3 ∙ 9 = 27
9 ∙ 3 = 27
27 = 27
9 ∙ 8 = 8 ∙ 9
Проверка:
9 ∙ 8 = 72
8 ∙ 9 = 72
72 = 72
5 ∙ 7 + 5 = 5 ∙ 9 – 5
Проверка:
5 ∙ 7 + 5 = 35 + 5 = 40
5 ∙ 9 – 5 = 45 – 5 = 40
40 = 40
8 ∙ 9 – 8 = 8 ∙ 7 + 8
Проверка:
8 ∙ 9 – 8 = 72 – 8 = 64
8 ∙ 7 + 8 = 56 + 8 = 64
64 = 64
3 ∙ 10 – 3 = 3 ∙ 8 + 3
Проверка:
3 ∙ 10 – 3 = 30 – 3 = 27
3 ∙ 8 + 3 = 24 + 3 = 27
27 = 27
7 ∙ 5 – 7 = 7 ∙ 3 + 7
Проверка:
7 ∙ 5 – 7 = 35 – 7 = 28
7 ∙ 3 + 7 = 21 + 7 = 28
28 = 28
Номер 6.
Альбом для рисования и карандаш стоят 15 р. На все свои деньги Оля может купить 1 альбом или 4 карандаша. Сколько денег у Оли? Реши подбором.
Ответ:
Внимательно читай условия задачи, перебирай возможные варианты её решения.
Оформляем условие в виде рисунка.
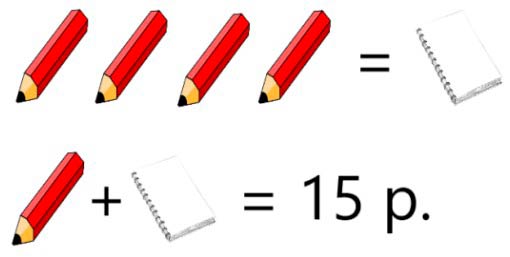
По условию задачи мы знаем, что стоимость 4 карандашей равна стоимости одного альбома. Также стоимость карандаша и альбома равна 15 рублей.
Рассуждаем.
Предположим, что карандаш стоит 1 рубль, тогда 1 ∙ 4 = 4 (р.) – стоимость альбома.
Сделаем проверку:
4 р + 1 р. - 5 р. – стоимость карандаша и альбома.
5 р. < 15 р.
А по условию задачи стоимость карандаша и альбома равна 15 рублей.
Значит, данный вариант не подходит.
Продолжаем рассуждение.
Предположим, что карандаш стоит 2 рубля, то 2 ∙ 4 = 8 (р.) – стоимость альбома.
Сделаем проверку:
8 р. + 2 р. = 10 р. – стоимость карандаша и альбома.
10 р. < 15 р.
А по условию задачи стоимость карандаша и альбома равна 15 рублей.
Значит, данный вариант не подходит.
Продолжаем рассуждение.
Предположим, что карандаш стоит 3 рубля, то 3 ∙ 4 = 12 (р.) – стоимость альбома.
12 р. + 3 р. = 15 р. – стоимость карандаша и альбома.
15 р. = 15 р.
Значит карандаш стоит 3 рубля, а альбом 12 рублей.
У Оли 12 рублей.
Записываем ответ.
Ответ: у Оли 12 рублей.
Задание внизу страницы
На одно окно требуется 3 одинаковых стекла. Сколько окон можно застеклить, если есть 10 таких стекол? 20 стекол?
Ответ:1 окно - 3 стекла
? окон - 10 стёкол
? окон - 20 стёкол
1) 10 : 3 = 3 (ок.) и (ост. 1 ст.)
2) 20 : 3 = 6 (ок.) и (ост. 2 ст.)
Ответ: 3 окна можно сделать из 10 стёкол; 6 окон можно сделать из 20 стёкол.
1) Вспомни как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Оформляем условие в виде краткой записи.
1 окно – 3 стекла
? окон – 10 стекол
? окон – 20 стекол
Рассуждаем.
На одно окно требуется 3 стекла. Чтобы узнать, сколько окон можно застеклить с помощью 10 стёкол и 20 стёкол, нужно общее количество стёкол разделить на количество стёкол, которое потребуется на одно окно.
1) 10 : 3 = 3 (ост. 1) = окон из 10 стекол.
Если разделить 10 стёкол на группы по 3 стекла, то получим 3 такие группы и ещё останется 1 стекло.
Значит, можно застеклить 3 окна и ещё 1 стекло останется.
2) 20 : 3 = 6 (ост. 2) – окон из 20 стекол.
Если разделить 20 стёкол на группы по 3 стекла, то получим 6 таких групп и ещё останется 2 стекла.
Значит, можно застеклить 6 окон и ещё 2 стекла останется.
Записываем ответ.
Ответ: 3 окна, 6 окон.
Задание на полях страницы
Вычисли. Найди лишнее выражение:

27 + 30 = 57 20 + 37 = 57 50 + 7 = 57 34 + 23 = 57 45 + 12 = 57 40 + 16 = 56 (Лишнее выражение)
Чтобы узнать, какое выражение лишнее, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Вычислим выражения.
27 + 30 = 57
20 + 37 = 57
50 + 7 = 57
34 + 23 = 57
45 + 12 = 57
40 + 16 = 56
Делаем вывод.
40 + 16 = 56 – лишнее, так как в остальных примерах сумма равна 57.
Номер 1.
Выполни деление с остатком и проверь:
Ответ:50 : 15 = 3 (ост. 5) Проверка: 1) 5 < 15 2) 15 · 3 + 5 = 50 18 : 27 = 0 (ост. 18) Проверка: 1) 18 < 27 2) 27 · 0 + 18 = 18 89 : 22 = 4 (ост. 1) Проверка: 1) 1 < 22 2) 22 · 4 + 1 = 89 75 : 18 = 4 (ост. 3) Проверка: 1) 3 < 18 2) 18 · 4 + 3 = 75 100 : 30 = 3 (ост. 10) Проверка: 1) 10 < 30 2) 30 · 3 + 10 = 100 76 : 20 = 3 (ост. 16) Проверка: 1) 16 < 20 2) 20 · 3 + 16 = 76 57 : 42 = 1 (ост. 15) Проверка: 1) 15 < 42 2) 42 · 1 + 15 = 57 28 : 17 = 1 (ост. 11) Проверка: 1) 11 < 17 2) 17 · 1 + 11 = 28 25 : 26 = 0 (ост. 25) Проверка: 1) 25 < 26 2) 26 · 0 + 25 = 25 9 : 13 = 0 (ост. 9) Проверка: 1) 9 < 13 2) 13 · 0 + 9 = 9
Вспомни, как выполнить проверку деления с остатком.
Рассуждаем.
Найдём частное методом подбора.
50 : 15 = ?
Надо 50 разделить на 15.
Пробуем в частном 3.
Проверим: 15 ∙ 3 = 45
50 – 45 = 5, 5 < 15, значит, частное 3, а остаток 5.
50 : 15 = 3 (ост. 5)
18 : 27 = ?
Надо 18 разделить на 27.
Так как 18 < 27, то целых частей нет.
18 : 27 = 0 (ост. 18)
89 : 22 = ?
Надо 89 разделить на 22.
Пробуем в частном 4.
Проверим: 22 ∙ 4 = 88
89 – 88 = 1, 1 < 22, значит, частное 4, а остаток 1.
89 : 22 = 4 (ост. 1)
75 : 18 = ?
Надо 75 разделить на 18.
Пробуем в частном 4.
Проверим: 18 ∙ 4 = 72
75 – 72 = 3, 3 < 18, значит, частное 4, а остаток 3.
75 : 18 = 4 (ост. 3)
100 : 30 = ?
Надо 100 разделить на 30.
Пробуем в частном 3.
Проверим: 30 ∙ 3 = 90
100 – 90 = 10, 10 < 30, значит, частное 3, а остаток 10.
100 : 30 = 3 (ост. 10)
57 : 42 = ?
Надо 57 разделить на 42.
Пробуем, например, в частном 1.
Проверим: 42 ∙ 1 = 42
Найдём остаток и сравним его с делителем:
57 – 42 = 15, 15 < 42, значит, частное 1, а остаток 15.
57 : 42 = 1 (ост. 5)
28 : 17 = ?
Надо 28 разделить на 17.
Пробуем, например, в частном 1.
Проверим: 17 ∙ 1 = 17
Найдём остаток и сравним его с делителем:
28 – 17 = 11, 11 < 17, значит, частное 1, а остаток 11.
28 : 17 = 1 (ост. 11)
76 : 20 = ?
Надо 76 разделить на 20.
Пробуем в частном 3.
Проверим: 20 ∙ 3 = 60
Найдём остаток и сравним его с делителем:
76 – 60 = 16, 16 < 20, значит, частное 3, а остаток 16.
76 : 20 = 3 (ост. 16)
25 : 26 = ?
Надо 25 разделить на 26.
Так как 25 < 26, то целых частей нет.
25 : 26 = 0 (ост. 25)
9 : 13 = 0 (ост. 9)
Надо 9 разделить на 13.
Так как 9 < 13, то целых частей нет.
Ответ: 9 : 13 = 0 (ост. 9)
Выполняем проверку и оформляем задание в тетрадь.
50 : 15 = 3 (ост. 5)
Проверка:
1) 5 < 15
2) 15 ∙ 3 + 5 = 45 + 5 = 50
18 : 27 = 0 (ост. 18)
Проверка:
1) 18 < 27
2) 27 ∙ 0 + 18 = 0 + 18 = 18
89 : 22 = 4 (ост. 1)
Проверка:
1) 1 < 22
2) 22 ∙ 4 + 1 = 88 + 1 = 89
75 : 18 = 4 (ост. 3)
Проверка:
1) 3 < 18
2) 18 ∙ 4 + 3 = 72 + 3 = 75
100 : 30 = 3 (ост. 10)
Проверка:
1) 10 < 30
2) 30 ∙ 3 + 10 = 90 + 10 = 100
57 : 42 = 1 (ост. 15)
Проверка:
1) 15 < 42
2) 42 ∙ 1 + 15 = 57
28 : 17 = 1 (ост. 11)
Проверка:
1) 11 < 17
2) 1 ∙ 17 + 11 = 28
76 : 20 = 3 (ост. 16)
Проверка:
1) 16 < 20
2) 3 ∙ 20 + 16 = 60 + 16 = 76
25 : 26 = 0 (ост. 25)
Проверка:
1) 25 < 26
2) 26 ∙ 0 + 25 = 0 + 25 = 25
9 : 13 = 0 (ост. 9)
Проверка:
9 < 13
13 ∙ 0 + 9 = 0 + 9 = 9
Номер 2.
Ответ:
а : b, значит, значение a нужно разделить на b.
Рассуждаем.
Представим данные выражения в виде уравнений.
72 : 2 = х
72 : 2 = (60 + 12) : 2 = 30 + 6 = 36
х = 36
72 : 3 = х
72 : 3 = (60 + 12) : 3 = 20 + 4 = 24
х = 24
х : 4 = 18
х = 18 ∙ 4
18 ∙ 4 = (10 + 8) ∙ 4 = 40 + 32 = 72
х = 72
х : 6 = 12
х = 12 ∙ 6
12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72
х = 72
х : 8 = 9
х = 9 ∙ 8
х = 72
72 : х = 72
х = 72 : 72
х = 1
72 : х = 1
х = 72 : 1
х = 72
Оформляем задание в тетрадь.
Подставим полученные значения в таблицу.
.jpg)
Номер 3.
Половину пути от дома до школы мальчик прошел за 15 мин, а на остальной путь он затратил на 6 мин больше. Сколько времени он затратил на весь путь до школы?
Ответ:
1) 15 + 6 = 21 (мин) – затратил на остальной путь. 2) 15 + 21 = 36 (мин) – всё время пути. Ответ: 36 минут затратил на весь путь мальчик.
«на 6 минут больше» - значит столько же, но ещё 6 минут.
Оформляем краткую запись в виде схематического рисунка.
.jpg)
Рассуждаем.
Вторая часть пути на 6 минут больше, чем первая половина. Значит, к первой части пути нужно прибавить 6.
15 + 6 = 21 (мин.) – затратил на остальной путь.
Продолжаем рассуждение.
Весь путь складывается из первой и второй половины пути. Значит, чтобы найти сколько времени мальчик затратил на весь путь, нужно сложить время первой половины пути и время второй половины пути.
15 + 21 = 36 (мин.) – затратил на весь путь.
Записываем ответ.
Ответ: 36 минут он затратил на весь путь до школы.
Номер 4.
Начерти квадрат, площадь которого равна 4 см2. Раскрась его четвертую часть. Покажи, как это можно сделать по-разному. Сколько квадратных сантиметров раскрашено? Чему равна площадь нераскрашенной части?
Ответ:
1 см2 – раскрашен. S нераскрашенной части 3 см2.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
3) Чтобы найти площадь квадрата нужно его сторону умножить два раза.
Рассуждаем.
Найдем сторону квадрата. Чтобы найти площадь квадрата, нужно его сторону умножить два раза и это произведение равно 4 см2. Значит, нужно подобрать такое число, которое при умножении само на себя в произведении равно 4. Это число 2. 2 ∙ 2 = 4 Значит сторона квадрата равна 2 см.
Продолжаем рассуждение.
Найдем площадь раскрашенной и нераскрашенной части.
Раскрашенная часть квадрата – это одна четвертая часть. Значит, квадрат нужно разделить на 4 части и взять одну такую часть.
4 см2 : 4 = 1 см2 – площадь раскрашенной части.
Весь квадрат состоит из раскрашенной части и нераскрашенной части. Значит, чтобы найти площадь нераскрашенной части, нужно из общей площади квадрата вычесть площадь раскрашенной части.
4 см2 – 1 см2 = 3 см2 – площадь нераскрашенной части.
Оформляем задание в тетрадь.
.jpg)
1 см2 – площадь раскрашенной части.
3 см2 – площадь нераскрашенной части.
Номер 5.
Ответ:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним деление методом подбора.
45 : 15 = ?
Надо 45 разделить на 15.
Пробуем в частном 3.
Проверяем: 15 ∙ 3 = (10 + 5) ∙ 3 = 30 + 15 = 45,
45 = 45, значит,
45 : 15 = 3.
99 : 33 = ?
Надо 99 разделить на 33.
Пробуем в частном 3.
Проверяем: 33 ∙ 3 = (30 + 3) ∙ 3 = 90 + 9 = 99,
99 = 99, значит,
99 : 33 = 3.
80 : 16 = ?
Надо 80 разделить на 16.
Пробуем в частном 5.
Проверяем: 16 ∙ 5 = (10 + 6) ∙ 5 = 50 + 30 = 80,
80 = 80, значит,
80 : 16 = 5.
Выполним вычисления по действиям.
78 : 6 ∙ 3 = 39
1) 78 : 6 = (60 + 18) : 6 = 60 : 6 + 18 : 6 = 10 + 3 = 13
2) 13 ∙ 3 = (10 + 3) ∙ 3 = 10 ∙ 3 + 3 ∙ 3 = 30 + 9 = 39
51 : 3 ∙ 4 = 68
1) 51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
2) 17 ∙ 4 = (10 + 7) ∙ 4 = 10 ∙ 4 + 7 ∙ 4 = 40 + 28 = 68
84 : 4 ∙ 3 = 63
1) 84 : 4 = (80 + 4) : 4 = 20 + 1 = 21
2) 21 ∙ 3 = (20 + 1) ∙ 3 = 20 ∙ 3 + 1 ∙ 3 = 60 + 3 = 63
100 – 2 ∙ 18 = 64
1) 2 ∙ 18 = 2 ∙ (10 + 8) = 2 ∙ 10 + 2 ∙ 8 = 20 + 16 = 36
2) 100 – 36 = 64
100 – 3 ∙ 18 = 46
1) 3 ∙ 18 = 3 ∙ (10 + 8) = 3 ∙ 10 + 3 ∙ 8 = 30 + 24 = 54
2) 100 – 54 = 46
100 – 4 ∙ 18 = 28
1) 4 ∙ 18 = 4 ∙ (10 + 8) = 4 ∙ 10 + 4 ∙ 8 = 40 + 32 = 72
2) 100 – 72 = 28
(34 + 36) : 10 = 7
1) 34 + 36 = 70
2) 70 : 10 = 7
(75 – 33) : 3 = 14
1) 75 – 33 = 42
2) 42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14
(82 – 16) : 33 = 2
1) 82 – 16 = 66
2) 66 : 33 = 2
Оформляем задание в тетрадь.
45 : 15 = 3
99 : 33 = 3
80 : 16 = 5
78 : 6 ∙ 3 = 13 ∙ 3 = 39
51 : 3 ∙ 4 = 17 ∙ 4 = 68
84 : 4 ∙ 3 = 21 ∙ 3 = 63
100 – 2 ∙ 18 = 100 – 36 = 64
100 – 3 ∙ 18 = 100 – 54 = 46
100 – 4 ∙ 18 = 100 – 72 = 28
(34 + 36) : 10 = 70 : 10 = 7
(75 – 33) : 3 = 42 : 3 = 14
(82 – 16) : 33 = 66 : 33 = 2
Номер 6.
Измерь стороны многоугольников в миллиметрах и найди периметр каждого из них.

Р1 = 24 ∙ 4 = 96 мм Р2 = 33 ∙ 3 = 99 мм Р3 = 15 ∙ 6 = 90 мм Ответ: 96 мм периметр первого многоугольника, 99 мм периметр второго многоугольника, 90 мм периметр третьего многоугольника.
Периметр фигуры – суммы длин всех ее сторон.
Для измерения сторон используй линейку.
Измерим стороны фигур.
Измерим с помощью линейки все стороны каждой фигуры.
Квадрат: все его стороны равны – 2 см 4 мм = 24 мм
Треугольник: все его стороны равны – 3 см 3 мм = 33 мм
Шестиугольник: все его стороны равны – 1 см 5 мм = 15 мм
Вычислим периметры.
Чтобы найти периметр нужно сложить все стороны данной фигуры:
Так как у квадрата 4 стороны, и они все равны, то:
1) 24 мм ∙ 4 = 96 мм = 9 см 6 мм – периметр квадрата.
Так как у данного треугольника 3 стороны, и они все равны, то:
2) 33 мм ∙ 3 = 99 мм = 9 см 9 мм – периметр треугольника.
Так как у данного шестиугольника 6 сторон, и они все равны, то:
3) 15 мм ∙ 6 = 90 мм = 9 см – периметр шестиугольника.
Оформляем задание в тетрадь.
1) 24 мм ∙ 4 = 96 мм – периметр квадрата.
2) 33 мм ∙ 3 = 99 мм – периметр треугольника.
3) 15 мм ∙ 6 = 90 мм – периметр шестиугольника.
Номер 7.
Используя только цифры 1, 2, 3, 4, 5, 6, 7 и не повторяя ни одну из них, составь такие 4 числа, чтобы при их сложении получилось 100.
Ответ:2 + 17 + 35 + 46 = 100 5 + 12 + 36 + 47 = 100 6 + 15 + 37 + 42 = 100 6 + 15 + 32 + 47 = 100 7 + 14 + 23 + 56 = 100 7 + 16 + 35 + 42 = 100
Внимательно рассмотри цифры и составь такие числа, чтобы их сумма была равна 100.
Рассуждаем.
Посмотри внимательно какие цифры в сумме дают число, оканчивающееся на 0. Комбинируй их. Цифры можно переставлять местами.
Выполняем задание.
Несколько возможных вариантов:
2 + 17 + 35 + 46 = 100
5 + 12 + 36 + 47 = 100
6 + 15 + 37 + 42 = 100
6 + 15 + 32 + 47 = 100
7 + 14 + 23 + 56 = 100
7 + 16 + 35 + 42 = 100
Задание внизу страницы
Выполни проверку деления с остатком.
Ответ:65 : 20 = 3(ост.5) 39 : 12 = 3(ост.3) Проверка Проверка 5 < 20 3 < 12 20 ∙ 3 + 5 = 65 12 ∙ 3 + 3 = 39
1) Повтори, как выполняется деление с остатком.
2) Повтори случаи вне табличного деления.
Рассуждаем.
Чтобы сделать проверку нужно:
1) убедиться, что остаток меньше делителя;
2) частное умножить на делитель и прибавить к произведению остаток, должно получиться делимое.
Если хотя бы один пункт не выполняется, то деление выполнено не верно.
Оформляем задание в тетрадь.
65 : 20 = 3 (ост. 5)
1) 5 < 20
2) 20 ∙ 3 + 5 = 60 + 5 = 65
39 : 12 = 3 (ост. 3)
1) 3 < 12
2) 12 ∙ 3 + 3 = 36 + 3 = 39
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.