Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 29

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Выполни деление с остатком.
Ответ:
1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Рассуждаем.
53 : 8 = ?
Если трудно вспомнить самое большое число до 53, которое делится на 8 без остатка, то частное можно найти способом подбора.
Надо 53 разделить на 8.
Пробуем, например, в частном 5.
Проверим: 8 ∙ 5 = 40.
Найдём остаток и сравним его с делителем:
53 - 40 = 13, 13 > 8, значит, 5 мало.
Пробуем в частном 6.
Проверим: 8 ∙ 6 = 48;
53 - 48 = 5, 5 < 8, значит, частное 6, а остаток 5.
Ответ: 53 : 8 = 6 (ост. 5)
78 : 9 = ?
Если трудно вспомнить самое большое число до 78, которое делится на 9 без остатка, то частное можно найти способом подбора.
Надо 78 разделить на 9.
Пробуем, например, в частном 7.
Проверим: 9 ∙ 7 = 63.
Найдём остаток и сравним его с делителем:
78 - 63 = 15, 15 > 9, значит, 7 мало.
Пробуем в частном 8.
Проверим: 9 ∙ 8 = 72;
78 - 72 = 6, 6 < 9, значит, частное 8, а остаток 6.
Ответ: 78 : 9 = 8 (ост. 6)
25 : 10 = ?
Если трудно вспомнить самое большое число до 25, которое делится на 10 без остатка, то частное можно найти способом подбора.
Надо 25 разделить на 10.
Пробуем, например, в частном 2.
Проверим: 10 ∙ 2 = 20.
Найдём остаток и сравним его с делителем:
25 - 20 = 5, 5 < 10, значит, частное 2, а остаток 5.
Ответ: 25 : 10 = 2 (ост. 5)
38 : 11 = ?
Если трудно вспомнить самое большое число до 38, которое делится на 11 без остатка, то частное можно найти способом подбора.
Надо 38 разделить на 11.
Пробуем, например, в частном 2.
Проверим: 11 ∙ 2 = 22.
Найдём остаток и сравним его с делителем:
38 - 22 = 16, 16 > 11, значит, 2 мало.
Пробуем в частном 3.
Проверим: 11 ∙ 3 = 33;
38 - 33 = 5, 5 < 11, значит, частное 3, а остаток 5.
Ответ: 38 : 11 = 3 (ост. 5)
50 : 20 = ?
Если трудно вспомнить самое большое число до 50, которое делится на 20 без остатка, то частное можно найти способом подбора.
Надо 50 разделить на 20.
Пробуем, например, в частном 2.
Проверим: 20 ∙ 2 = 40.
Найдём остаток и сравним его с делителем:
50 - 40 = 10, 10 < 20, значит, частное 2, а остаток 10.
Ответ: 50 : 20 = 2 (ост. 10)
Выполняем вычисления и оформляем задание в тетрадь.
Выполним деление в столбик.
53 : 8 = 6 (ост. 5)
.jpg)
78 : 9 = 8 (ост. 6)
.jpg)
25 : 10 = 2 (ост. 5)
.jpg)
38 : 11 = 3 (ост. 5)
.jpg)
50 : 20 = 2 (ост. 10)
.jpg)
Номер 2.
На аэродроме 20 самолетов. Сколько всего троек самолетов может подняться в воздух? Сколько при этом самолетов останется на земле?
Ответ:Всего – 20 с. Троек в воздухе – ? с. Останется на земле – ? с. 20 : 3 = 6 (ост. 2) Ответ: 6 троек самолётов могут подняться в небо, на земле останется 2 самолёта.
1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Оформляем условие в виде рисунка или краткой записи.
Рисунок.

Краткая запись.
Всего – 20 самолетов
В воздухе – ? троек
На земле – ?
Рассуждаем.
Если разделить 20 самолётов на группы по 3 самолёта, то получим 6 таких групп и ещё останется 2 самолёта. Значит, 6 троек самолётов могут подняться в небо, на земле останется 2 самолёта.
20 : 3 = 6 (ост. 2)
Записываем ответ.
Ответ: 6 троек самолетов, 2 самолета останется.
Номер 3.
В пекарне за 3 дня израсходовали 48 мешков муки. (Ежедневный расход муки один и тот же.) На сколько дней хватит 80 мешков муки, если ежегодный расход муки не изменится? Составь задачу, обратную данной, и реши ее.
Ответ:
1) 48 : 3 = 16 (м.) – муки расходует за 1 день.
2) 80 : 16 = 5 (д.) – на столько хватит 80 м муки.
Ответ: 80 кг муки пекарне хватит на 5 дней.
Обратная задача:

В пекарне за 3 дня израсходовали 48 мешков муки. Сколько было мешков муки, если их израсходовали за 5 дней. 1) 48 : 3 = 16 (м.) – муки расходовали за один день. 2) 5 ∙ 16 = 80 (м.) – муки было. Ответ: 80 мешков муки было в пекарне.
1) Обратная задача – это задача с одинаковом сюжетом, где нужно узнать то, что в изначальной задаче известно, то есть известное и неизвестное меняются местами.
2) Данная задача: вида «кол-во дней, ежедневный расход, общее кол-во мешков» характеризуется зависимостями между компонентами:
Кол-во дней · ежедневный расход = общее кол-во мешков.
Общее кол-во мешков : кол-во дней = ежедневный расход.
Общее кол-во мешков : ежедневный расход = кол-во дней.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Из таблицы видно, что общее количество мешков складывается из количества мешков, расходуемых в каждый день. Поэтому, чтобы узнать, сколько расходуется мешков на каждый день, нужно общее количество мешков разделить на количество дней.
48 : 3 = (30 + 18) : 3 = 10 + 6 = 16 (м.) – ежедневный расход муки.
Продолжаем рассуждение.
Чтобы узнать, на сколько дней хватит 80 мешков муки, нужно общее количества мешков разделить на ежедневный расход.
80 : 16 = 5 (д.) – на сколько хватит 80 мешков муки.
Записываем ответ.
Ответ: на 5 дней.
Решение выражением: 80 : (48 : 3) = 80 : 16 = 5 (д.) – на сколько хватит 80 мешков муки, где 48 : 3 – ежедневный расход муки.
Составляем условие обратной задачи.
За 5 дней израсходовали 80 мешков муки. Ежедневный расход муки один и тот же. Сколько мешков муки понадобится на 3 дня?
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
Из таблицы видно, что общее количество мешков складывается из количества мешков, расходуемых в каждый день. Поэтому, чтобы узнать, сколько расходуется мешков на каждый день, нужно общее количество мешков разделить на количество дней.
80 : 5 = (50 + 30) : 5 = 10 + 6 = 16 (м) – ежедневный расход.
Продолжаем рассуждение.
Чтобы узнать сколько муки понадобится на 3 дня, ежедневный расход умножить на количество дней.
16 ∙ 3 = (10 + 6) ∙ 3 = 30 + 18 = 48 (м.) – на 3 дня.
Записываем ответ.
Ответ: 48 мешков муки.
Решение выражением:
80 : 5 ∙ 3 = 16 ∙ 3 = 48 (м.) – на 3 дня, где 80 : 5 – ежедневный расход муки.
Номер 4.
Уменьши на 18 числа: 30, 48, 70, 98. Уменьши в 9 раз числа: 27, 90, 72, 54.
Ответ:30 – 18 = 12
48 – 18 = 30
70 – 18 = 52
98 – 18 = 80
27 : 9 = 3
90 : 9 = 10
72 : 9 = 8
54 : 9 = 6
1) Уменьшить на 18, значит, из числа вычесть 18 единиц.
2) Уменьшить в 9 раз, значит, нужно данное число разделить на 9.
Рассуждаем.
Уменьшим числа на 18.
Уменьшить на 18, значит, из данного числа вычесть число 18:
30 – 18 = 12
48 – 18 = 30
70 – 18 = 52
98 – 18 = 80
Продолжаем рассуждение.
Уменьшим числа в 9 раз.
Уменьшить в 9 раз, значит, данное число разделить на 9:
27 : 9 = 3
90 : 9 = 9 дес. : 9 = 1 дес. = 10
72 : 9 = 8
54 : 9 = 6
Номер 5.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
1 3 2
38 : 19 + 42 : 3 = 16
1) 38 : 19 = 2 – вычисляем методом подбора
2) 42 : 3 = (30 + 12) : 3 = 10 + 4 = 14
3) 2 + 14 = 16
1 2 3
16 · 6 : 3 − 30 = 2
1) 16 ∙ 6 = (10 + 6) ∙ 6 = 60 + 36 = 96
2) 96 : 3 = (90 + 6) : 3 = 30 + 2 = 32
3) 32 – 30 = 2
1 2 3
28 : 2 ∙ 3 + 8 = 50
1) 28 : 2 = (20 + 8) : 2 = 10 + 4 = 14
2) 14 ∙ 3 = (10 + 4) ∙ 3 = 30 + 12 = 42
3) 42 + 8 = 50
1 2
(47 + 8) : 11 = 5
1) 47 + 8 = 55
2) 55 : 11 = 5 – методом подбора
1 2
(86 – 72) ∙ 5 = 70
1) 86 – 72 = 14
2) 14 ∙ 5 = (10 + 4) ∙ 5 = 50 + 20 = 70
2 1
90 – 9 : 9 = 89
1) 9 : 9 = 1
2) 90 – 1 = 89
2 1
3 ∙ (72 – 60) = 36
1) 72 – 60 = 12
2) 3 ∙ 12 = 3 ∙ (10 + 2) = 30 + 6 = 36
2 1
4 ∙ (91 – 80) = 44
1) 91 – 80 = 11
2) 4 ∙ 11 = 44
2 1
82 – 25 : 5 = 77
1) 25 : 5 = 5
2) 82 – 5 = 77
Оформляем задание в тетрадь.
1 3 2
38 : 19 + 42 : 3 = 2 + 14 = 16
1 2 3
16 · 6 : 3 − 30 = 96 : 3 − 30 = 32 − 30 = 2
1 2 3
28 : 2 ∙ 3 + 8 = 14 ∙ 3 + 8 = 42 + 8 = 50
1 2
(47 + 8) : 11 = 55 : 11 = 5
1 2
(86 – 72) ∙ 5 = 14 ∙ 5 = 70
2 1
90 – 9 : 9 = 90 – 1 = 89
2 1
3 ∙ (72 – 60) = 3 ∙ 12 = 36
2 1
4 ∙ (91 – 80) = 4 ∙ 11 = 44
2 1
82 – 25 : 5 = 82 – 5 = 77
Номер 6.
Оля, Петя и Катя принесли к столу 3 вазы с фруктами. В вазах у Оли и Пети было по 3 яблока, в вазах у Оли и Кати – по 6 груш. Кто какие вазы принес?
Ответ:Оля принесла вазу, в которой 6 груш и 3 яблока, Катя принесла вазу с 1 яблоком и 6 грушами, а Петя – с 3 яблоками и 8 грушами. Ответ: 1 ваза - Петя, 2 ваза - Катя, 3 ваза - Оля.
Внимательно прочитай задачу и рассмотри вазы с фруктами.
Рассмотрим вазы.
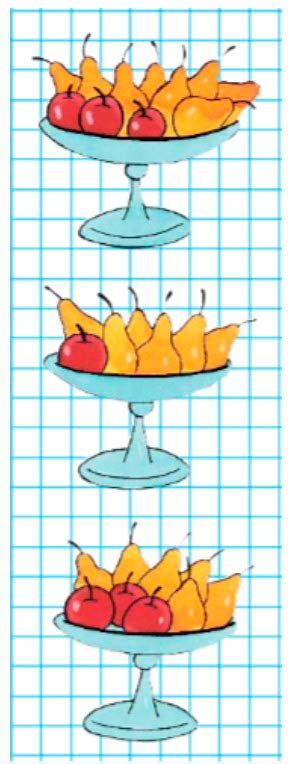
1 ваза: 3 яблока и 8 груш
2 ваза: 1 яблоко и 6 груш
3 ваза: 3 яблока и 6 груш
Рассуждаем.
По условию задачи у Оли и Пети было по 3 яблока, значит, Катя принесла вазу №2 в которой 1 яблоко и 6 груш.
Продолжаем рассуждение.
Также по условию задачи у Оли и Кати по 6 груш, значит у Пети ваза №1 с 8 грушами, а у Оли ваза №3.
Записываем ответ.
Петя – 1 ваза – 3 яблока и 8 груш;
Катя – 2 ваза – 1 яблоко и 6 груш;
Оля – 3 ваза – 3 яблока и 6 груш.
Задание внизу страницы
Ответ:43 : 8 = 5 (ост.3) 64 : 7 = 9 (ост.1)
1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Рассуждаем.
Выполним вычисления методом подбора.
43 : 8 = ? (ост. ?)
Если трудно вспомнить самое большое число до 43, которое делится на 8 без остатка, то частное можно найти способом подбора. Надо 43 разделить на 8. Пробуем в частном 2. Проверим: 8 ∙ 2 = 16.
Найдём остаток и сравним его с делителем: 43 – 16 =27, 27 > 8, значит 2 мало.
Пробуем в частном 3. Проверим: 8 ∙ 3 = 24.
Найдем остаток и сравним его с делителем: 43 – 24 = 19, 19 > 8, значит 3 мало.
Пробуем в частном 4. Проверим: 8 ∙ 4 = 32.
Найдем остаток и сравним его с делителем: 43 – 32 = 11, 11 > 8, значит 4 мало.
Пробуем в частном 5. Проверим: 8 ∙ 5 = 40.
Найдем остаток и сравним его с делителем: 43 – 40 = 3, 3 < 8, значит частное 5, а остаток 3.
Ответ: 43 : 8 = 5 (ост. 3)
64 : 7 = ? (ост. ?)
64 не делится на 7 без остатка. Вспомним, какое самое большое число до 64 делится на 7 без остатка. Это 63.
Найдем частное: 63 : 7 = 9.
Найдем остаток: 64 – 63 = 1.
Ответ: 64 : 7 = 9 (ост. 1)
Записываем ответ.
Оформим деление столбиком.
43 : 8 = 5 (ост. 3)
.jpg)
64 : 7 = 9 (ост. 1)
.jpg)
Задание вверху страницы.
1) Для изготовления рамки требуется 4 одинаковые деревянные планки. Сколько таких рамок можно сделать из 16 таких планок? из 10 планок? 2) Сколько таких рамок можно сделать, если есть только 3 планки?
Ответ:Задача 1:

1) 16 : 4 = 4 (р.) – из 16 планок.
2) 10 : 4 = 2 (ост. 2) (р.) – из 10 планок.
Ответ: 4 рамки можно сделать из 16 планок, 2 рамки можно сделать из 10 планок.
Задача 2:
1) 3 : 4 = 0 (р.)(ост.3)
Ответ: 0 рамок можно сделать из 3 планок.
Ни одной рамки нельзя сделать из трёх планок.
1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Оформляем условие в виде таблицы.
-(2024).jpg)
Рассуждаем.
На одну рамку требуется 4 планки. Чтобы узнать, сколько рамок можно изготовить из нужного количества планок, нужно общее количество планок разделить на количество планок для 1 рамки.
16 : 4 = 4 (р.) – можно изготовить из 16 планок.
10 : 4 = 2 (ост. 2) – рамки можно изготовить из 10 планок и ещё 2 планки останутся.
Записываем ответ.
Ответ: 4 рамки; 2 рамки.
Рассуждаем.
Для одной рамки требуется 4 планки, а по условию планок только 3.
3 < 4, значит сделать рамку нельзя.
Продолжаем рассуждение.
Рассмотрим решение.
-(2024).jpg)
Так как 3 < 4, то целых частей нет.
Из трех планок нельзя сделать ни одной рамки и 3 планки останутся.
Записываем ответ.
Ответ: 0 планок.
Номер 1.
Ручка стоит 3 р. Сколько таких ручек можно купить на 10 р.? на 5 р.? на 1 р.?
Ответ:10 : 3 = 3 (ост. 1) – 3 ручки можно купить на 10 р., останется 1 р. 5 : 3 = 1 (ост. 2) – 1 ручку можно купить на 5 р., останется 2 р. 1 : 3 = 0 (ост. 1) – ни одной ручки нельзя купить на 1 р.
1) Вспомни, как выполнить деление с остатком.
2) Помни, что остаток должен быть меньше делителя.
Оформляем краткую запись.
1 ручка – 3 р.
? ручек – 10 р.
? ручек – 5 р.
? ручек – 1 р.
Рассуждаем.
Одна ручка стоит 3 рубля. Чтобы узнать, сколько ручек можно купить на определенное количество денег, нужно общее количество денег разделить на стоимость 1 ручки.
1) 10 : 3 = 3 (ост. 1) – ручки можно купить на 10 рублей.
Если разделить 10 рублей на группы по 3 рубля, то получим 3 такие группы и ещё останется 1 рубль.
Значит, можно купить 3 ручки и ещё 1 рубль останется.
2) 5 : 3 = 1 (ост. 2) – ручку можно купить на 5 рублей.
Если разделить 5 рублей на группы по 3 рубля, то получим 1 такую группу и ещё останется 2 рубля.
Значит, можно купить 1 ручку и ещё 2 рубля останется.
3) 1 : 3 = 0 (ост. 1) – невозможно купить ручки на 1 рубль.
Разделить 1 рубль на группы по 3 рубля не получится, так как 1 < 3.
Значит, купить ручки на 1 рубль нельзя.
Записываем ответ.
Ответ: на 10 рублей можно купить 3 ручки; на 5 рублей – 1 ручку; на 1 рубль – нельзя купить ни одной ручки.
Номер 2.
Какое самое большое число до числа 40 делится без остатка на 9? на 7? на 6?
Ответ:36 : 9 = 4 35 : 7 = 5 36 : 6 = 6
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Рассуждаем.
40 не делится на 9 без остатка. Вспомним, какое самое большое число до 40 делится на 9 без остатка. Это 36.
36 : 9 = 4
40 не делится на 7 без остатка. Вспомним, какое самое большое число до 40 делится на 7 без остатка. Это 35.
35 : 7 = 5
40 не делится на 6 без остатка. Вспомним, какое самое большое число до 40 делится на 6 без остатка. Это 36.
36 : 6 = 6
Оформляем задание в тетрадь.
36 : 9 = 4
35 : 7 = 5
36 : 6 = 6
Номер 3.
Привезли 36 досок. Когда несколько досок взяли на ремонт сарая, осталось 27 досок. Во сколько раз больше осталось досок, чем израсходовали? На сколько меньше досок израсходовали, чем осталось?
Ответ:
1) 36 – 27 = 9 (д.) – взяли. 2) 27 : 9 = 3 – во столько раз больше досок осталось, чем взяли. 3) 27 – 9 = 18 (д.) – на столько меньше досок израсходовали, чем осталось. Ответ: в 3 раза больше досок осталось, чем взяли; на 18 досок меньше израсходовали, чем осталось.
1) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
2) Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Общее количество досок складывается из досок, которые остались и которые израсходовали. Значит, чтобы найти, сколько досок израсходовали, нужно из общего количества досок вычесть доски, которые остались.
36 – 27 = 9 (д.) – израсходовали.
Продолжаем рассуждение.
Осталось 27 досок, а израсходовали – 9 досок. Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Значит, нужно количество досок, которые остались, разделить на количество досок, которые израсходовали.
27 : 9 = 3 (р.) – во столько раз больше досок осталось, чем израсходовали.
Продолжаем рассуждение.
Осталось 27 досок, а израсходовали – 9 досок. Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее. Значит, нужно из количества досок, которые остались, вычесть количество досок, которые израсходовали.
27 – 9 = 18 (д.) – на столько меньше досок израсходовали, чем осталось.
Записываем ответ.
Ответ: в 3 раза больше; на 18 досок меньше.
Номер 4.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
1) В данных выражениях присутствуют действия умножение и деление – они равноправны. Поэтому выполняем действия по порядку слева направо.
72 : 9 ∙ 12 = 96
1) 72 : 9 = 8
2) 8 ∙ 12 = 8 ∙ (10 + 2) = 80 + 16 = 96
64 : 8 ∙ 11 = 88
1) 64 : 8 = 8
2) 8 ∙ 11 = 88
81 : 9 ∙ 11 = 99
1) 81 : 9 = 9
2) 9 ∙ 11 = 99
56 : 7 ∙ 10 = 80
1) 56 : 7 = 8
2) 8 ∙ 10 = 80
9 ∙ 9 : 3 = 27
1) 9 ∙ 9 = 81
2) 81 : 3 = (60 + 21) : 3 = 20 + 7 = 27
7 ∙ 8 : 2 = 28
1) 7 ∙ 8 = 56
2) 56 : 2 = (40 + 16) : 2 = 20 + 8 = 28
8 ∙ 9 : 4 = 18
1) 8 ∙ 9 = 72
2) 72 : 4 = (40 + 32) : 4 = 10 + 8 = 18
6 ∙ 8 : 3 = 16
1) 6 ∙ 8 = 48
2) 48 : 3 = (30 + 18) : 3 = 10 + 6 = 16
2) В данных выражениях вначале расставим порядок действий, а потом выполним вычисления по действиям.
2 1
63 : (14 − 7) = 9
1) 14 – 7 = 7
2) 63 : 7 = 9
1 2
(30 – 12) : 6 = 3
1) 30 – 12 = 18
2) 18 : 6 = 3
2 1
27 : (38 – 35) = 9
1) 38 – 35 = 3
2) 27 : 3 = 9
1 2
(98 – 8) : 5 = 18
1) 98 – 8 = 90
2) 90 : 5 = (50 + 40) : 5 = 10 + 8 = 18
1 3 2
9 ∙ 3 – 12 : 4 = 24
1) 9 ∙ 3 = 27
2) 12 : 4 = 3
3) 27 – 3 = 24
1 3 2
36 : 6 + 4 ∙ 6 = 30
1) 36 : 6 = 6
2) 4 ∙ 6 = 24
3) 6 + 24 = 30
1 3 2
32 : 4 + 6 ∙ 8 = 56
1) 32 : 4 = 8
2) 6 ∙ 8 = 48
3) 8 + 48 = 56
1 3 2
9 ∙ 7 – 54 : 6 = 54
1) 9 ∙ 7 = 63
2) 54 : 6 = 9
3) 63 – 9 = 54
3 1 2
80 – 32 : 8 : 2 = 78
1) 32 : 8 = 4
2) 4 : 2 = 2
3) 80 – 2 = 78
1 2 3
(80 – 32) : 8 : 2 = 3
1) 80 – 32 = 48
2) 48 : 8 = 6
3) 6 : 2 = 3
3 2 1
80 – 32 : (8 : 2) = 72
1) 8 : 2 = 4
2) 32 : 4 = 8
3) 80 – 8 = 72
3 1 2
36 + 24 : 6 ∙ 2 = 44
1) 24 : 6 = 4
2) 4 ∙ 2 = 8
3) 36 + 8 = 44
Оформляем задание в тетрадь.
1)
72 : 9 ∙ 12 = 8 ∙ 12 = 96
64 : 8 ∙ 11 = 8 ∙ 11 = 88
81 : 9 ∙ 11 = 9 ∙ 11 = 99
56 : 7 ∙ 10 = 8 ∙ 10 = 80
9 ∙ 9 : 3 = 81 : 3 = 27
7 ∙ 8 : 2 = 56 : 2 = 28
8 ∙ 9 : 4 = 72 : 4 = 18
6 ∙ 8 : 3 = 48 : 3 = 16
2)
2 1
63 : (14 − 7) = 63 : 7 = 9
1 2
(30 – 12) : 6 = 18 : 6 = 3
2 1
27 : (38 – 35) = 27 : 3 = 9
1 2
(98 – 8) : 5 = 90 : 5 = 18
1 3 2
9 ∙ 3 – 12 : 4 = 27 – 3 = 24
1 3 2
36 : 6 + 4 ∙ 6 = 6 + 24 = 30
1 3 2
32 : 4 + 6 ∙ 8 = 8 + 48 = 56
1 3 2
9 ∙ 7 – 54 : 6 = 63 – 9 = 54
3 1 2
80 – 32 : 8 : 2 = 80 – 4 : 2 = 80 – 2 = 78
1 2 3
(80 – 32) : 8 : 2 = 48 : 8 : 2 = 6 : 2 = 3
3 2 1
80 – 32 : (8 : 2) = 80 – 32 : 4 = 80 – 8 = 72
3 1 2
36 + 24 : 6 ∙ 2 = 36 + 4 ∙ 2 = 36 + 8 = 44
Номер 5.
Найди значения выражения 88 : m при m = 4, m = 8, m = 2, m = 1.
Ответ:88 : m m = 4 88 : 4 = 22 m = 8 88 : 8 = 11 m = 2 88 : 2 = 44 m = 1 88 : 1 = 88
1) 88 : m, значит, число 88 нужно разделить на m.
2) Помни, что 10 = 1 дес.
Рассуждаем.
88 : m, если:
m = 4, то:
88 : 4 = (80 + 8) : 4 = 80 : 4 + 8 : 4 = 20 + 2 = 22
Число 88 представим в виде суммы чисел 80 и 8, каждое слагаемое разделим на 4 и полученные результаты сложим.
m = 8, то:
88 : 8 = (80 + 8) : 8 = 80 : 8 + 8 : 8 = 10 + 1 = 11
Число 88 представим в виде суммы чисел 80 и 8, каждое слагаемое разделим на 8 и полученные результаты сложим.
m = 2, то:
88 : 2 = (80 + 8) : 2 = 80 : 2 + 8 : 2 = 40 + 4 = 44
Число 88 представим в виде суммы чисел 80 и 8, каждое слагаемое разделим на 2 и полученные результаты сложим.
m = 1, то:
88 : 1 = 88.
Если число разделить на единицу, то получится это число.
Оформляем задание в тетрадь.
88 : m, если:
m = 4, то 88 : 4 = 22
m = 8, то 88 : 8 = 11
m = 2, то 88 : 2 = 44
m = 1, то 88 : 1 = 88.
Номер 6.
Реши уравнения и сделай проверку.
Ответ:
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Рассмотрим уравнения.
х : 23 = 4
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
х ∙ 14 = 84
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
96 : х = 24
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно значение делимого разделить на значение частного.
Решим уравнение.
х : 23 = 4
х = 23 ∙ 4
23 ∙ 4 = (20 + 3) ∙ 4 = 80 + 12 = 92
х = 92
х ∙ 14 = 84
х = 84 : 14
х = 6
96 : х = 24
х = 96 : 24
х = 4
Сделаем проверку.
В уравнение вместо неизвестного подставим найденное значение.
х : 23 = 4
Проверка: вместо неизвестного подставим число 92.
92 : 23 = 4 – методом подбора.
4 = 4
х ∙ 14 = 84
Проверка: вместо неизвестного подставим число 6.
6 ∙ 14 = 6 ∙ (10 + 4) = 60 + 24 = 84
84 = 84
96 : х = 24
Проверка: вместо неизвестного подставим число 4.
96 : 4 = (80 + 16) : 4 = 20 + 4 = 24
24 = 24
Оформляем задание в тетрадь.
х : 23 = 4
х = 23 ∙ 4
х = 92
Проверка:
92 : 23 = 4
4 = 4
х ∙ 14 = 84
х = 84 : 14
х = 6
Проверка:
6 ∙ 14 = 84
84 = 84
96 : х = 24
х = 96 : 24
х = 4
Проверка:
96 : 4 = 24
24 = 24
Номер 7.
В каком уравнении каждой пары значение х будет больше? Подтверди свои ответы.
Ответ:19 ∙ х = 57
19 ∙ х = 76
Если в примерах на умножение есть один одинаковый множитель, то второй будет больше в том, где произведение больше. Значит, х будет больше в примере 19 ∙ х = 76.
40 : х = 4
40 : х = 8
Если в примерах на деление есть один одинаковые делимые, то делитель тогда будет больше, когда частное будет меньше. Значит, х будет больше в примере 40 : х = 4.
х : 3 = 18
х : 3 = 24
Если в примерах на деление есть один одинаковые делители, то делимое в том случае будет больше, когда частное больше. Значит, х будет больше в примере х : 3 = 24.
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Сравним уравнения.
1 пара:
19 ∙ х = 57
19 ∙ х = 76
Если первый множитель у двух примеров одинаковы, то второй множитель больше у того, у которого больше произведение.
Первый множитель в обоих уравнениях – 19.
Произведение в 1 уравнении – 57.
Произведение во 2 уравнении – 76.
76 > 57, значит во 2 уравнении второй множитель больше.
2 пара:
40 : х = 4
40 : х = 8
В примерах на деление, если два делимых одинаковы, то больше тот делитель, в примере которого частное будет меньше.
Делимое в обоих уравнениях – 40
Частное в 1 уравнении – 4
Частное во 2 уравнении – 8
8 > 4, значит в 1 уравнении делитель больше.
3 пара:
х : 3 = 18
х : 3 = 24
В примерах на деление, если два делителя одинаковы, то больше то делимое в примере, у которого частное больше.
Делитель в обоих уравнениях – 3
Частное в 1 уравнении – 18
Частное во 2 уравнении – 24
24 > 18, значит делимое во втором уравнении больше.
Делаем проверку.
1 пара:
19 ∙ х = 57
х = 57 : 19
х = 3
3 < 4
19 ∙ х = 76
х = 76 : 19
х = 4
Во втором уравнении неизвестное больше.
2 пара:
40 : х = 4
х = 40 : 4
х = 10
10 > 5
40 : х = 8
х = 40 : 8
х = 5
В первом уравнении неизвестное больше.
3 пара:
х : 3 = 18
х = 18 : 3
х = 6
8 > 6
х : 3 = 24
х = 24 : 3
х = 8
В первом уравнении неизвестное больше.
Оформляем задание в тетрадь.
19 ∙ х = 57
19 ∙ х = 76
Если первый множитель у двух примеров одинаковы, то второй множитель больше у того, у которого больше произведение.
Значит, х будет больше в примере 19 ∙ х = 76.
40 : х = 4
40 : х = 8
В примерах на деление, если два делимых одинаковы, то больше тот делитель, в примере которого частное будет меньше.
Значит, х будет больше в примере 40 : х = 4.
х : 3 = 18
х : 3 = 24
В примерах на деление, если два делителя одинаковы, то больше то делимое в примере, у которого частное больше.
Значит, х будет больше в примере х : 3 = 24.
Задание на полях страницы
Ребусы:


1) Вспомни, как выполняется деление с остатком;
2) Вспомни названия компонентов действия деления, а также – зависимость между компонентами и результатами действия умножения и деления.
Рассуждаем.
62 не делится на 9 без остатка.
Найдём неполное делимое: 9 ∙ 6 = 54
Найдём остаток: 62 – 54 = 8
Продолжаем рассуждения.
39 не делится на 6 без остатка.
Найдём неполное делимое: 39 – 3 = 36
Найдём остаток: 39 – 36 = 3
Записываем ответ.
62 : 9 = 6 (ост. 8)
39 : 6 = 6 (ост. 3)
-(2024).jpg)
Задание внизу страницы
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.