Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 25

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 7.
Поставь скобки, чтобы равенства стали верными.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставим скобки и порядок действий.
1 2
(100 − 24) : 2 = 38
1 2
36 : (6 + 3) = 4
1 2 3
(48 − 20) : 4 · 5 = 35
2 1 3
30 : (5 · 6) + 29 = 30
Сделаем проверку и вычисления по действиям.
1 2
(100 − 24) : 2 = 38
1) 100 – 21 = 76
2) 76 : 2 = (60 + 18) : 2 = 30 + 8 = 38
1 2
36 : (6 + 3) = 4
1) 6 + 3 = 9
2) 36 : 9 = 4
1 2 3
(48 − 20) : 4 · 5 = 35
1) 48 – 20 = 28
2) 28 : 4 = 7
3) 7 ∙ 5 = 35
2 1 3
30 : (5 · 6) + 29 = 30
1) 5 ∙ 6 = 30
2) 30 : 30 = 1
3) 1 + 29 = 30
Оформляем задание в тетрадь.
1 2
(100 − 24) : 2 = 76 : 2 = 38
1 2
36 : (6 + 3) = 36 : 9 = 4
1 2 3
(48 − 20) : 4 · 5 = 28 : 4 · 5 = 7 · 5 = 35
2 1 3
30 : (5 · 6) + 29 = 30 : 30 + 29 = 1 + 29 = 30
Номер 8.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Выполним вычисления способом умножения или деления суммы на число.
32 ∙ 3 = (30 + 2) ∙ 3 = 30 ∙ 3 + 2 ∙ 3 = 90 + 6 = 96
Представим число 32 в виде суммы 30 и 2. Умножим каждое слагаемое на 3 и полученные результаты сложим.
62 : 2 = (60 + 2) : 2 = 60 : 2 + 2 : 2 = 30 + 1 = 31
Представим число 62 в виде суммы 60 и 2. Разделим каждое слагаемое на 2 и полученные результаты сложим.
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
Представим число 24 в виде суммы 20 и 4. Умножим каждое слагаемое на 3 и полученные результаты сложим.
Выполним вычисления по действиям.
(96 + 4) : 20 = 5
1) 96 + 4 = 100
2) 100 : 20 = 10 дес. : 2 дес. = 10 : 2 = 5
(31 − 7) : 24 = 1
1) 31 − 7 = 24
2) 24 : 24 = 1
72 : 8 ∙ 11 = 99
1) 72 : 8 = 9
2) 9 ∙ 11 = 99
98 − 33 ∙ 2 = 32
1) 33 ∙ 2 = 66
2) 98 − 66 = 32
100 − 2 ∙ 19 = 62
1) 2 ∙ 19 = 2 ∙ (10 + 9) = 20 + 18 = 38
2) 100 - 38 = 62
9 ∙ 9 + 17 = 98
1) 9 ∙ 9 = 81
2) 81 + 17 = 98
Оформляем задание в тетрадь.
32 ∙ 3 = (30 + 2) ∙ 3 = 30 ∙ 3 + 2 ∙ 3 = 90 + 6 = 96
62 : 2 = (60 + 2) : 2 = 60 : 2 + 2 : 2 = 30 + 1 = 31
24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
(96 + 4) : 20 = 100 : 20 = 5
(31 − 7) : 24 = 24 : 24 = 1
72 : 8 ∙ 11 = 72 : 8 ∙ 11 = 99
98 − 33 ∙ 2 = 98 − 66 = 32
100 − 2 ∙ 19 = 100 − 38 = 62
9 ∙ 9 + 17 = 81 + 17 = 98
Номер 9.
Ответ:

1) a · b, значит, значение a нужно умножить на b.
2) c : d, значит, значение c нужно разделить на d.
Рассуждаем.
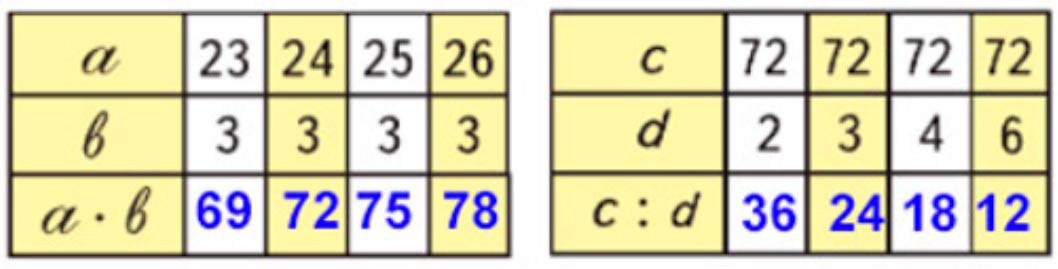
Таблица 1.
a ∙ b, если
а = 23, b = 3, то 23 ∙ 3 = (20 + 3) ∙ 3 = 20 ∙ 3 + 3 ∙ 3 = 60 + 9 = 69
а = 24, b = 3, то 24 ∙ 3 = (20 + 4) ∙ 3 = 20 ∙ 3 + 4 ∙ 3 = 60 + 12 = 72
а = 25, b = 3, то 25 ∙ 3 = (20 + 5) ∙ 3 = 20 ∙ 3 + 5 ∙ 3 = 60 + 15 = 75
а = 26, b = 3, то 23 ∙ 3 = (20 + 6) ∙ 3 = 20 ∙ 3 + 6 ∙ 3 = 60 + 18 = 78
При вычислении выражений используем правило умножения суммы на число.
Таблица 2.
с : d, если
с = 72, d = 2, то 72 : 2 = (60 + 12) : 2 = 60 : 2 + 12 : 2 = 30 + 6 = 36
с = 72, d = 3, то 72 : 3 = (60 + 12) : 3 = 60 : 3 + 12 :3 = 20 + 4 = 24
с = 72, d = 4, то 72 : 4 = (40 + 32) : 4 = 40 : 4 + 32 : 4 = 10 + 8 = 18
с = 72, d = 6, то 72 : 6 = (60 + 12) : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12
При вычислении выражений используем правило деления суммы на число.
Заполним таблицы.
Номер 10.
Для изготовления 5 одинаковых скворечников потребовалось заготовить 20 прямоугольных и 10 квадратных дощечек. Сколько всего дощечек идет на 1 скворечник?
Ответ:5 скв. – 20 и 10 д.
1 скв. – ? д.
1-й способ решения:
1) 20 + 10 = 30 (д.) – на 5 скворечников.
2) 30 : 5 = 6 (д.) – на один скворечник.
Ответ: 6 дощечек идёт на изготовления одного скворечника.
2-й способ решения:
1) 20 : 5 = 4 (шт.) – прямоугольных дощечек потребовалось.
2) 10 : 5 = 2 (шт.) – квадратных дощечек потребовались.
3) 2 + 4 = 6 (д.) – потребовалось всего.
Ответ: 6 дощечек идёт на изготовления одного скворечника.
3-й способ решения:
(20 + 10) : 5 = 30 : 5 = 6 (шт.) – дощечек для 1 скворечника
или
20 : 5 + 10 : 5 = 2 + 4 = 6 (шт.) – дощечек для 1 скворечника
Ответ: 6 дощечек.
Решение задачи сводится к применению правила деления суммы на число:
1) Чтобы разделить сумму на число можно вычислить сумму и разделить её на число;
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Оформляем условие в виде краткой записи.
5 сквор. – 20 пр. д. и 10 кв. д. 1 сквор. – ?
Рассуждаем.
Узнаем, сколько всего дощечек понадобилось для 5 одинаковых скворечников.
Общее количество дощечек складывается из прямоугольных и квадратных дощечек.
20 + 10 = 30 (шт.) – всего дощечек понадобилось для 5 скворечников.
Продолжаем рассуждение.
Узнаем, сколько дощечек понадобится для 1 скворечника.
Мы теперь знаем, что для 5 скворечников понадобилось 30 дощечек. При чём все скворечники одинаковые. Значит, чтобы найти сколько дощечек нужно для 1 скворечника нужно общее количество дощечек разделить на количество скворечников.
30 : 5 = 6 (шт.) – нужно дощечек для 1 скворечника.
Записываем ответ.
Ответ: 6 дощечек.
Решение выражением:
(20 + 10) : 5 = 6 (шт.) – дощечек для 1 скворечника, где 20 + 10 – количество дощечек для 5 скворечников.
Рассуждаем.
Узнаем сколько по отдельности прямоугольных и квадратных дощечек понадобится для одного скворечника.
Все скворечники одинаковые. Значит, чтобы найти сколько отдельно дощечек каждого вида нужно для 1 скворечника нужно общее количество дощечек каждого вида разделить на количество скворечников.
20 : 5 = 4 (шт.) – понадобится прямоугольных дощечек для 1 скворечника.
10 : 5 = 2 (шт.) – понадобится квадратных дощечек для 1 скворечника.
Продолжаем рассуждение.
Узнаем сколько всего дощечек нужно для 1 скворечника.
Общее количество дощечек для 1 скворечника складывается из прямоугольных и квадратных дощечек – это вычисляется сложением.
4 + 2 = 6 (шт.) – дощечек на 1 скворечник.
Записываем ответ.
Ответ: 6 дощечек.
Решение выражением:
20 : 5 + 10 : 5 = 6 (шт.) – дощечек для 1 скворечника,
где 20 : 5 – прямоугольных дощечек; 10 : 5 – квадратных дощечек.
Номер 11.
Дети играли в слова. Маша составила 9 слов, а Слава – 27 других слов. Во сколько раз больше слов составил Слава, чем Маша? На сколько у Славы больше слов, чем у Маши?
Ответ:
1) 27 : 9 = 3 (р.) – во столько слов больше у Славы. 2) 27 – 9 = 18 (сл.) – на столько больше у Славы. Ответ: в 3 раза больше слов составил Слава, чем Маша; на 18 слов больше у Славы, чем у Маши.
1) «во сколько раз больше» – вычисляется делением;
2) «на сколько больше», – вычисляется вычитанием.
Оформляем условие в виде краткой записи.
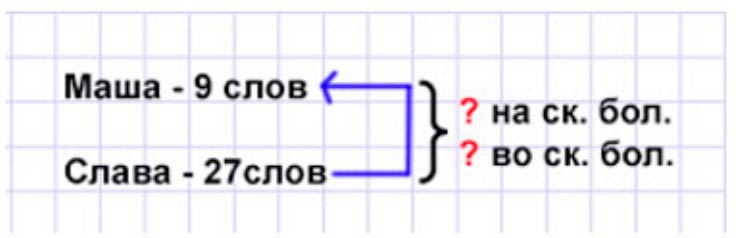
Рассуждаем.
Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее.
Значит, чтобы узнать, во сколько раз больше Слава составил слов, чем Маша, нужно количество Славиных слов разделить на количество Машиных слов.
27 : 9 = 3 – во столько больше.
Продолжаем рассуждение.
Чтобы узнать, на сколько больше слов составил Слава, чем Маша, нужно из количества Славиных слов вычесть количество Машиных.
27 − 9 = 18 – на столько больше.
Записываем ответ.
Ответ: в 3 раза больше, на 18 слов больше.
Номер 12.
Ответ:1)
.jpg)
1-й способ решения:
2) 0 : 8 = 0 17 ∙ 1 = 17 24 : 1 = 24
0 ∙ 8 = 0 17 + 0 = 17 24 – 0 = 24
2-й способ решения:
: 8 = 0
Если частное равно 0, значит и делимое тоже равняется 0.
0 : 8 = 0
· 8 = 0
Если произведение равно 0, значит один из множителей тоже равен 0.
0 · 8 = 0
17 · = 17
Число не изменится, если умножить его на 1.
17 · 1 = 17
17 + = 17
Число не изменится, если к нему прибавить 0.
17 + 0 = 17
24 : = 24
Число не изменится, если его разделить на 1.
24 : 1 = 24
24 - = 24
Число не изменится, если из него вычесть 0.
24 – 0 = 24
1) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
2) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Расставляем порядок действий и выполняем вычисления.
1) Выполним вычисления способом деления суммы на число.
36 : 3 = (30 + 6) : 3 = 30 : 3 + 6 : 3 = 10 + 2 = 12
Число 36 представим в виде суммы 30 и 6. Каждое слагаемое разделим на 3 и полученные результаты сложим.
82 : 2 = (80 + 2) : 2 = 80 : 2 + 2 : 2 = 40 + 1 = 41
Число 82 представим в виде суммы 80 и 2. Каждое слагаемое разделим на 2 и полученные результаты сложим.
42 : 3 = (30 + 12) : 3 = 30 : 3 + 12 : 3 = 10 + 4 = 14
Число 42 представим в виде суммы 30 и 12. Каждое слагаемое разделим на 3 и полученные результаты сложим.
78 : 6 = (60 + 18) : 6 = 60 : 6 + 18 : 6 = 10 + 3 = 13
Число 78 представим в виде суммы 60 и 18. Каждое слагаемое разделим на 6 и полученные результаты сложим.
30 : 2 = (20 + 10) : 2 = 20 : 2 + 10 : 2 = 10 + 5 = 15
Число 30 представим в виде суммы 20 и 10. Каждое слагаемое разделим на 2 и полученные результаты сложим.
74 : 2 = (60 + 14) : 2 = 60 : 2 + 14 : 2 = 30 + 7 = 37
Число 74 представим в виде суммы 60 и 14. Каждое слагаемое разделим на 2 и полученные результаты сложим.
Выполним вычисления по действиям.
65 − 64 : 8 ∙ 3 = 41
1) 64 : 8 = 8
2) 8 ∙ 3 = 24
3) 65 − 24 = 41
9 ∙ (14 − 9) − 8 = 37
1) 14 − 9 = 5
2) 9 ∙ 5 = 45
3) 45 − 8 = 37
2) Найдём значение неизвестного с помощью рассуждений.
: 8 = 0
Если частное равно 0, значит и делимое тоже равняется 0.
0 : 8 = 0
Ответ: 0.
∙ 8 = 0
Если произведение равно 0, значит один из множителей тоже равен 0.
0 ∙ 8 = 0
Ответ: 0.
17 ∙ = 17
Число не изменится, если умножить его на 1.
17 ∙ 1 = 17
Ответ: 1.
17 + = 17
Число не изменится, если к нему прибавить 0.
17 + 0 = 17
Ответ: 0.
24 : = 24
Число не изменится, если его разделить на 1.
24 : 1 = 24
Ответ: 1.
24 − = 24
Число не изменится, если из него вычесть 0.
24 − 0 = 24
Ответ: 0.
Оформляем задание в тетрадь.
1)
36 : 3 = (30 + 6) : 3 = 10 + 2 = 12
82 : 2 = (80 + 2) : 2 = 40 + 1 = 41
42 : 3 = (30 + 12) : 3 = 10 + 4 = 14
78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
30 : 2 = (20 + 10) : 2 = 10 + 5 = 15
74 : 2 = (60 + 14) : 2 = 30 + 7 = 37
65 − 64 : 8 ∙ 3 = 65 − 8 ∙ 3 = 65 − 24 = 41
9 ∙ (14 − 9) − 8 = 9 ∙ 5 − 8 = 45 − 8 = 37
2)
: 8 = 0
0 : 8 = 0
Ответ: 0.
∙ 8 = 0
0 ∙ 8 = 0
Ответ: 0.
17 ∙ = 17
17 ∙ 1 = 17
Ответ: 1.
17 + = 17
17 + 0 = 17
Ответ: 0.
24 : = 24
24 : 1 = 24
Ответ: 1.
24 − = 24
24 − 0 = 24
Ответ: 0.
Номер 13.
Определи без измерений, где чей прямоугольник, если Витя начертил прямоугольник, площадь которого на 2 см2 меньше, чем площадь прямоугольника у Кости, но в 2 раза больше, чем площадь прямоугольника у Севы.

Синий прямоугольник Костин, красный прямоугольник Севы, зеленый прямоугольник Вити.
Площадь – часть плоскости, которую занимает фигура.
Оформляем условие в виде схематического рисунка.
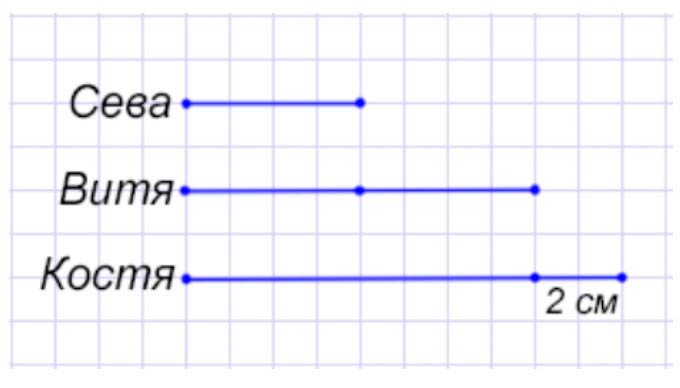
Рассуждаем.
Рассмотрим прямоугольники.
1 прямоугольник (синий) больше, чем 2 прямоугольник (зеленый) и больше, чем 3 третий прямоугольник (розовый).
2 прямоугольник меньше, чем 3 прямоугольник.
Синий пр. > Розовый пр.
Синий пр. > Зеленый пр.
Зеленый пр. > Розовый пр.
Расставим прямоугольники по возрастанию площади: розовый, зеленый, синий.
Продолжаем рассуждение.
У Вити прямоугольник меньше по площади, чем у Кости на 2 , значит у Кости площадь прямоугольника больше, чем у Вити.
У Вити прямоугольник по площади больше, чем у Севы в 2 раза.
Расставим мальчиков по возрастанию нарисованных прямоугольников: По Сева, Витя, Костя.
Делаем вывод.
Костя начертил синий прямоугольник (первый)
Сева начертил розовый прямоугольник (второй)
Витя начертил зеленый прямоугольник (третий).
Задание на полях страницы
Ребусы:



Вспомни названия компонентов действия сложения и вычитанием, умножения и деления, а также – зависимость между компонентами и результатами действий.
Рассуждаем.
Количетво единиц второго слагаемого неизвестно. Но чтобы узнать количество единиц второго слагаемого, нужно из единиц значения суммы вычесть количество единиц первого слагаемого.
Из 4 ед. мы не можем вычесть 8 ед., значит занимаем 1 дес. = 10 ед.,
10 + 4 = 14 ед.
14 ед. – 8 ед. = 6 ед.
Значит, во втором слагаемом 6 единиц.
Продолжаем рассуждение.
Количество десяток в первом слагаемом неизвестно. Но чтобы узнать чему равно количество десятков первого слагаемого, нужно из количества десятков значения суммы вычесть количесвто десятков второго слагаемого.
5 дес. – 2 дес. = 3 дес. и ещё 1 дес. занимали, осталось 3 дес. – 1 дес. = 2 дес.
Значит, в первом слагаемом 2 десятка.
Записываем ответ.
Получим равенство: 28 + 26 = 54.
Запишем равенство в столбик:
.jpg)
Рассуждаем.
Количество единиц уменьшаемого неизвестно. Но количество единиц уменьшаемого можно узнать, если сложить количество единиц вычитаемого и разности.
Тогда, 2 ед. + 8 ед. = 10 ед – это 1 дес. 0 ед.
Значит, в уменьшаемом 0 единицы.
Продолжаем рассуждение.
Количество десятков вычитаемого неизвестно. Но количество десятков вычитаемого можно узнать, если из количества десятков уменьшаемого вычесть количество десятков значения разности.
8 дес. – 1 дес. = 6 дес. и ещё 1 дес. занимали, осталось 6 дес. – 1 дес. = 5 дес.
Значит, в вычитаемом 5 десятков.
Записываем ответ.
Получим равенство: 70 – 52 = 18.
Запишем равенство в столбик:
.jpg)
Рассуждаем.
3 ребус. Нужно вспомнить, когда произведение двух однозначных чисел равно числу, которое оканчивается на 1.
4 ребус. Нужно вспомнить, когда произведение двух однозначных чисел равно числу, которое оканчивается на 6.
5 ребус. Нужно вспомнить, когда произведение двух однозначных чисел равно числу, которое оканчивается на 4.
Рассмотрим возможные варианты.
3 ребус. Возможные варианты:
3 ∙ 7 = 21
7 ∙ 3 = 81
9 ∙ 9 = 81
4 ребус. Возможные варианты.
2 ∙ 8 = 16
8 ∙ 2 = 16
4 ∙ 4 = 16
6 ∙ 6 = 36
4 ∙ 9 = 36
9 ∙ 4 = 36
7 ∙ 8 = 56
8 ∙ 7 = 56
5 ребус. Возможные варианты.
2 ∙ 7 = 14
7 ∙ 2 = 14
3 ∙ 8 = 24
8 ∙ 3 = 24
4 ∙ 6 = 24
6 ∙ 4 = 24
8 ∙ 8 = 64
9 ∙ 6 = 54
6 ∙ 9 = 54
Запишем ответ.
Представлен один из вариантов решения. Все остальные возможные варианты находятся выше.
.jpg)
Номер 1.
1) Найди частное и остаток, используя рисунки. Объясни, почему при делении на 2 в остатке может быть только 0 или 1. 2) Сделай рисунки и выполни деление. 3) Объясни, почему при делении на 3 остаток не может быть равен 5.

1) 9 : 2 = 4 (ост. 1) 10 : 2 = 5 11 : 2 = 5 (ост. 1) Остаток всегда меньше делителя.

3) При делении на 3 остаток не может быть равен 5, потому что остаток всегда должен быть меньше делителя, а 5 > 3.
Вспомни, как выполнить деление с остатком.
Рассуждаем.
Рассмотрим рисунки.
-(2024).jpg)
9 треугольников разделили на группы по 2 треугольника, получилось 4 полные группы и одна неполная группа с одним треугольником.
-(2024).jpg)
10 квадратов разделили на группы по 2 квадрата, получилось 5 полных групп.
-(2024).jpg)
11 шариков разделили на группы по 2 шарика, получилось 5 полных групп и одна неполная группа с одним шариком.
Выполним вычисления.
9 : 2 = 4 (ост. 1)
Частное – 4, остаток – 1
10 : 2 = 5 (ост. 0)
Частное – 5, остаток – 0
11 : 2 = 5 (ост. 1)
Частное – 5, остаток – 1
Делаем вывод.
При делении на 2 остаток может быть только 0 или 1, так как остаток всегда меньше делителя.
Выполним рисунки по выражениям.
-(2024).jpg)
Вычислим.
-(2024).jpg)
1) 6 разделить на 3, получится 2 и 0 в остатке.
2) 7 разделить на 3, получится 2 и 1 в остатке.
3) 8 разделить на 3, получится 2 и 2 в остатке.
4) 9 разделить на 3, получится 3 и 0 в остатке.
5) 10 разделить на 3, получится 3 и 1 в остатке.
Рассуждаем.
Рассмотрим выражения, в Задании 2.
При делении на 3 получается остаток только 0, 1 или 2. Получается, что остаток всегда меньше делителя.
Делаем вывод.
При делении на 3 остаток не может быть равен 5, так как 5 > 3, а остаток всегда должен быть меньше делителя.
Номер 2.
1) В хозяйстве у фермера 12 парников занято огурцами. Это составляет пятую часть всех его парников. Сколько парников у фермера? 2) Сколько всего килограммов огурцов собирал этот фермер за один день, если с каждого парника он собирал по 8 кг огурцов?
Ответ:Задача 1:

12 ∙ 5 = 60 (п.)
Ответ: всего у фермера 60 парников.
Задача 2:
1 парник – 8 кг
12 парников – ? кг
12 ∙ 8 = 96 (кг)
Ответ: 96 кг огурцов собрал фермер с парников всего.
1) Доля – одна часть из тех, на которые разделили целое.
2) Первое слово в названии долей указывает на количество долей, которые взяли, а второе – на сколько частей разделили целое.
Оформляем условие в виде схематического рисунка.
.jpg)
Рассуждаем.
Сколько всего парников у фермера неизвестно, но пятая часть равна 12 парников. Каждая часть одинаковая, поэтому чтобы узнать, сколько всего парников, нужно количество парников в одной части умножить на количество этих частей.
12 ∙ 5 = (10 + 2) ∙ 5 = 10 ∙ 5 + 2 ∙ 5 = 50 + 10 = 60 (п.) – всего у фермера.
Записываем ответ.
Ответ: 60 парников у фермера.
Оформляем краткую запись.
1 парник – 8 кг
12 парников – ? кг
Рассуждаем.
Известно, что с одного парника можно собрать 8 кг огурцов и количество парников. Чтобы узнать, сколько всего собрали огурцов, нужно количество парников умножить на количество огурцов в одном парнике.
12 ∙ 8 = (10 + 2) ∙ 8 = 80 + 16 = 96 (кг) – огурцов собирал за день.
Записываем ответ.
Ответ: 96 кг огурцов собирал фермер за один день.
Номер 3.
На решение задачи и уравнений ученик затратил 25 мин. Сколько уравнений он решил, если на решение задачи он затратил 10 мин, а на решение каждого уравнения – по 5 мин?
Ответ:
1) 25 – 10 = 15 (мин.) – потратил ученик на уравнения. 2) 15 : 5 = 3 (шт.) – количество уравнений. Ответ: 3 уравнения решил ученик всего.
Общее время составляет из времени, на которое потратили на решение уравнений и решения задачи.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Из условий задачи известно, что ученик затратил 25 минут на задачу и уравнения, из которых10 минут на задачу. Чтобы узнать, сколько времени он потратил на уравнения, нужно из общего времени вычесть время, которое потратил ученик на задачу.
25 – 10 = 15 (мин.) – затратил на все уравнения.
Продолжаем рассуждение.
Мы узнали, что на все уравнения ученик потратил 15 минут, и что каждое уравнение он решал 5 минут. Значит, решение каждого уравнения заняло одинаковое время. Поэтому, чтобы узнать, сколько уравнений решил ученик, нужно время, потраченное на решение всех уравнений, разделить на время, потраченное на одно уравнение.
15 : 5 = 3 (ур.) – решил ученик.
Записываем ответ.
Ответ: 3 уравнения решил ученик.
Решение выражением: (25 – 10) : 5 = 15 : 5 = 3 (ур.) – решил ученик, где 25 – 10 – время, потраченное на решение всех уравнений.
Номер 4.
Ответ:92 : 46 = 2 24 : 8 ∙ 7 = 21
44 : 11 = 4 36 : 6 ∙ 8 = 48
60 : 12 = 5 42 : 7 ∙ 3 = 18
20 + 3 ∙ 4 = 32 28 + 64 – 14 = 78
80 – 5 : 5 = 79 75 – 32 – 20 = 23
40 – 26 : 2 = 27 16 + 76 – 36 = 56
1) Помни о порядке выполнения арифметических действий;
2) Сначала выполняются действия умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Вспомни деление методом подбора.
Расставляем порядок действий и выполняем вычисления.
Выполним деление методом подбора.
92 : 46 = 2
Пробуем в частном 2 и проверяем:
46 ∙ 2 = (40 + 6) ∙ 2 = 80 + 12 = 92
92 = 92, значит,
92 : 46 = 2
44 : 11 = 4
Пробуем в частном 4 и проверяем:
11 ∙ 44 = 44
44 = 44, значит,
44 : 11 = 4
60 : 12 = 5
Пробуем в частном 4 и проверяем:
12 ∙ 4 = (10 + 2) ∙ 4 = 40 + 8 = 48, 48 < 60, число 4 не подходит.
Пробуем в частном 5 и проверяем:
12 ∙ 5 = (10 + 2) ∙ 5 = 50 + 10 = 60
60 = 60, значит,
60 : 12 = 5
Выполним вычисления по действиям.
1 2
24 : 8 · 7 = 21
1) 24 : 8 = 3
2) 3 ∙ 7 = 21
1 2
36 : 6 ∙ 8 = 48
1) 36 : 6 = 6
2) 6 ∙ 8 = 48
1 2
42 : 7 ∙ 3 = 18
1) 42 : 7 = 6
2) 6 ∙ 3 = 18
2 1
20 + 3 ∙ 4 = 32
1) 3 ∙ 4 = 12
2) 20 + 12 = 32
2 1
80 − 5 : 5 = 79
1) 5 : 5 = 1
2) 80 – 1 = 79
2 1
40 – 26 : 2 = 27
1) 26 : 2 = (20 + 6) : 2 = 10 + 3 = 13
2) 40 – 13 = 27
1 2
28 + 64 – 14 = 78
1) 28 + 64 = 92
2) 92 – 14 = 78
1 2
75 – 32 – 20 = 23
1) 75 – 32 = 43
2) 43 – 20 = 23
1 2
16 + 76 – 36 = 56
1) 16 + 76 = 92
2) 92 – 36 = 56
Оформляем задание в тетрадь.
92 : 46 = 2
44 : 11 = 4
60 : 12 = 5
24 : 8 ∙ 7 = 3 ∙ 7 = 21
36 : 6 ∙ 8 = 6 ∙ 8 = 48
42 : 7 ∙ 3 = 6 ∙ 3 = 18
20 + 3 ∙ 4 = 20 + 12 = 32
80 – 5 : 5 = 80 – 1 = 79
40 – 26 : 2 = 40 – 13 = 27
28 + 64 – 14 = 92 – 14 = 78
75 – 32 – 20 = 43 – 20 = 23
16 + 76 – 36 = 92 – 36 = 56
Номер 5.
1) Назови номера фигур, в которых есть острые углы. 2) Есть ли различия в записях выражений для определения периметров фигур 1 и 2 и периметров фигур 3 и 4?

1) Фигуры 2 и 4.
2) Р1 = 22 · 4 = 88 мм.
Р2 = 19 · 4 = 76 мм.
Р3 = (34 + 22) · 2 = 112 мм.
Р4 = (26 + 19) · 2 = 90 мм.
Различий в записях выражений для определения периметров фигур 1 и 2 нет, так как у этих фигур все стороны равны.
Различий в записях выражений для определения периметров фигур 3 и 4 нет, так как у этих фигур две противоположные стороны равны между собой.
1) Тупой угол – больше 90º;
2) Прямой угол – равен 90º;
3) Острый угол – меньше 90º.
4) Периметр – это сумма длин всех сторон.
Рассуждаем.
С помощью угольника можно определить вид угла, если одна сторона угольника совпадает со стороной угла, а другая сторона угла находится внутри угольника, то такой угол острый.
Рассмотрим фигуры:
1) Это фигура – квадрат, у него все углы прямые.
2) Это фигура – ромб, к него два острых угла и два тупых угла.
3) Это фигура – прямоугольник, у него все углы прямые.
4) Это фигура – четырёхугольник, у него два острых и два тупых угла.
Делаем вывод.
Острый угол есть у фигур под № 2 и № 4.
Рассуждаем.
Измерим с помощью линейки все стороны данных фигур.
Фигура 1 – это квадрат со стронной 2 см 2 мм = 22 мм. У квадрата все стороны равны.
Периметр квадрата можно вычислить по формуле – сторону квадрата умножить на 4.
а ∙ 4 – формула периметра квадрата, где а – сторона квадрата.
Фигура 2 – это ромб со стороной 1 см 9 мм = 19 мм. У ромба все стороны равны.
Периметр ромба можно вычислить по формуле – сторону ромба умножить на 4.
а ∙ 4 – формула периметра ромба, где а – сторона ромба.
Фигура 3 – прямоугольник со сторонами 3 см 4 мм = 34 мм и 2 см 2 мм = 22 мм.
У прямоугольника стороны попарно равны, то есть противоположные стороны равны.
Периметр прямоугольника можно вычислить по формуле – сумма длины и ширины умножить на 2.
(а + b) ∙ 2 – формула периметра прямоугольника, где а и b – длина и ширина прямоугольника.
Фигура 4 – фигура с равными сторонами 2 см 6 мм = 26 мм и 1 см 9 мм = 19 мм
Периметр данной фигуры можно вычислить по формуле – сумму сторон умножить на 2.
(а + b) ∙ 2 – формула периметра прямоугольника, где а и b – длинны сторон.
Делаем вывод.
Различий в записях выражений для определения периметров фигур 1 и 2 нет, так как этих фигур все стороны равны.
Различий в записях выражений для определения периметров фигур 3 и 4 нет, так как у этих фигур две противоположные стороны равны между собой.
Вычисляем.
22 мм ∙ 4 = 88 мм = 8 см 8 мм – периметр фигуры 1
22 ∙ 4 = (20 + 2) ∙ 4 = 80 + 8 = 88
19 мм ∙ 4 = 76 мм = 7 см 6 мм – периметр фигуры 2
19 ∙ 4 = (10 + 9) ∙ 4 = 40 + 36 = 76
(34 мм + 22 мм) ∙ 2 = 56 мм ∙ 2 = 112 мм = 11 см 2 мм – периметр фигуры 3
56 ∙ 2 = (50 + 6) ∙ 2 = 100 + 12 = 112
(26 мм + 19 мм) ∙ 2 = 45 мм ∙ 2 = 90 мм = 9 см – периметр фигуры 4.
45 ∙ 2 = (40 + 5) ∙ 2 = 80 + 10 = 90
Задание внизу страницы
Почему при делении на 4 остаток не может быть равен 4, 5?
Ответ:При делении на 4 остаток не может быть равен 4 или 5, потому что остаток всегда должен быть меньше делителя, а 4 = 4 и 5 > 4.
1) Помни, что при делении остаток всегда должен быть меньше делителя.
2) При делении остаток всегда должен быть меньше делителя.
3) При делении остаток всегда должен быть меньше делителя.
4) Помни, что при делении остаток всегда должен быть меньше делителя.
Рассуждаем.
Если остаток равен 4 или 5, то он делится на 4:
4 : 4 = 1
5 : 4 = 1 (ост. 1)
Остаток всегда должен быть меньше делителя, значит, остаток при делении на 4 может быть только 0, 1, 2 или 3.
Делаем вывод.
При делении на 4 остаток не может быть равен 4 или 5, потому что остаток всегда должен быть меньше делителя, а 4 = 4 и 5 > 4.
Задание на полях страницы
Сравни. Найди лишнюю фигуру.

Все фигуры являются четырехугольниками, у них 4 угла и 4 стороны.
В фигуре 2 и 4 нет прямых углов, а в фигурах 1 и 3 есть.
Фигура 4 – лишняя, так как данную фигуру ещё не проходили.
Помни, что фигуры называют по количеству углов.
Рассмотрим фигуры.
1) Это фигура – квадрат, у него 4 прямых угла и 4 стороны.
2) Это фигура – ромб, у него два острых угла и два тупых угла, и 4 стороны.
3) Это фигура – прямоугольник, у него 4 прямых угла и 4 стороны.
4) Это фигура – четырёхугольник, у него два острых и два тупых угла, и 4 стороны.
Делаем вывод.
Все фигуры состоят из 4 сторон и 4 углов – они являются четырехугольниками.
Фигуры под № 1 и 3 – состоят из 4 прямых углов.
Фигуры под № 2 и 4 – состоят из 2 острых углов и 2 тупых углов.
Найдём лишнюю фигуру.
Фигура 4 – лишняя, так как данную фигуру ещё не проходили.
№ 1 – квадрат
№ 2 – ромб
№ 3 – прямоугольник
№ 4 – ?
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.