Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 21

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Из данных уравнений выпиши и реши те, которые решаются делением.
Ответ:
Уравнение – равенство, которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
Рассмотрим уравнения.
х : 18 = 5
х – неизвестное делимое.
Чтобы найти неизвестное делимое нужно значение частного умножить на делитель.
Решается умножением.
96 : х = 16
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
х : 15 = 6
х – неизвестное делимое.
Чтобы найти неизвестное делимое нужно значение частного умножить на делитель.
Решается умножением.
х ∙ 11 = 55
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Решается делением.
52 : х = 13
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
15 ∙ х = 75
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
Решается делением.
Решаем уравнение.
Решим уравнения, которые решаются делением.
х ∙ 11 = 55
х = 55 : 11
х = 5
Ответ: 5.
96 : х = 16
х = 96 : 16
х = 6
Ответ: 6.
52 : х = 13
х = 52 : 13
х = 4
Ответ: 4.
15 ∙ х = 75
х = 75 : 15
х = 5
Ответ: 5.
Делаем проверку.
х ∙ 11 = 55
Проверка: вместо х подставим число 5.
1) 11 ∙ 5 = (10 + 1) ∙ 5 = 50 = 5 = 55
2) 55 = 55
Уравнение решено верно.
96 : х = 16
Проверка: вместо х подставим число 6.
1) 96 : 6 = (60 + 36) : 6 = 10 + 6 = 16
2) 16 = 16
Уравнение решено верно.
52 : х = 13
Проверка: вместо х подставим число 4.
1) 52 : 4 = (40 + 12) : 4 = 10 = 3 = 13
2) 13 = 13
Уравнение решено верно.
15 ∙ х = 75
Проверка: вместо х подставим число 5.
1) 15 ∙ 5 = (10 + 5) 5 = 50 + 25 = 75
2) 75 = 75
Уравнение решено верно.
Номер 2.
Увеличь в 8 раз числа: 12, 9, 8, 11. Увеличь на 8 числа: 26, 37, 49, 58.
Ответ:12 ∙ 8 = 96
9 ∙ 8 = 72
8 ∙ 8 = 64
11 ∙ 8 = 88
26 + 8 = 34
37 + 8 = 45
49 + 8 = 57
58 + 8 = 66
1) Увеличь на 8, значит, прибавить 8 единиц.
2) Увеличь в 8 раз, значит, умножить на 8.
Увеличим числа в 8 раз.
12 ∙ 8 = (10 + 2) ∙ 8 = 10 ∙ 8 + 2 ∙ 8 = 80 + 16 = 96
9 ∙ 8 = 72
8 ∙ 8 = 64
11 ∙ 8 = 88
Увеличим числа на 8.
26 + 8 = 34
37 + 8 = 45
49 + 8 = 57
58 + 8 = 66
Номер 3.
Ответ:66 : 33 = 2 64 : 16 = 4 77 : 7 = 11
55 : 11 = 5 75 : 25 = 3 34 : 2 = 17
51 : 3 = 17 6 ∙ 12 = 72
84 : 7 = 12 98 : 2 = 49
1) Вспомни способ деления методом подбора.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Вычислим деление методом подбора.
66 : 33 = ?
Пробуем в частном 2 и проверяем: 33 ∙ 2 = 66, 66 = 66, значит 66 : 33 = 2.
Ответ: 2.
55 : 11 = ?
Пробуем в частном 4 и проверяем: 11 ∙ 4 = 44, 44 < 55, число 4 не подходит.
Пробуем в частном 5 и проверяем: 11 ∙ 5 = 55, 55 = 55, значит 55 : 11 = 5.
Ответ: 5.
64 : 16 = ?
Пробуем в частном 3 и проверяем: 16 ∙ 3 = 48, 48 < 64, число 3 не подходит.
Пробуем в частном 4 и проверяем: 16 ∙ 4 = 64, 64 = 64, значит 64 : 16 = 4.
Ответ: 4.
75 : 25 = ?
Пробуем в частном 2 и проверяем: 25 ∙ 2 = 50, 50 < 75, число 2 не подходит.
Пробуем в частном 3 и проверяем: 25 ∙ 3 = 75, 75 = 75, значит 75 : 25 = 3.
Ответ: 3.
Применим метод деления числа на сумму.
77 : 7 = (70 + 7) : 7 = 10 + 1 = 11
Представим число 70 в виде суммы чисел 70 и 7, каждое слагаемое разделим на 7 и полученные результаты сложим.
34 : 2 = (20 + 14) : 2 = 20 : 2 + 14 : 2 =10 + 7 = 17
Представим число 34 в виде суммы чисел 20 и 14, каждое слагаемое разделим на 2 и полученные результаты сложим.
51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
Представим число 51 в виде суммы чисел 30 и 21, каждое слагаемое разделим на 3 и полученные результаты сложим.
84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12
Представим число 84 в виде суммы чисел 70 и 14, каждое слагаемое разделим на 7 и полученные результаты сложим.
6 ∙ 12 = 6 ∙ (10 + 2) = 6 ∙ 10 + 6 ∙ 2 = 60 + 12 = 72
Представим число 12 в виде суммы чисел 10 и 2, каждое слагаемое умножим на 6 и полученные результаты сложим.
98 : 2 = (80 + 18) : 2 = 80 : 2 + 18 : 2 = 40 + 9 = 49
Представим число 98 в виде суммы чисел 80 и 18, каждое слагаемое разделим на 2 и полученные результаты сложим.
Оформляем задание в тетрадь.
66 : 33 = 2, так как 33 ∙ 2 = 66
55 : 11 = 5, так как 11 ∙ 5 = 55
64 : 16 = 4, так как 16 ∙ 4 = 64
75 : 25 = 3, так как 25 ∙ 3 = 75
77 : 7 = 11
34 : 2 = (20 + 14) : 2 = 20 : 2 + 14 : 2 =10 + 7 = 17
51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12
6 ∙ 12 = 6 ∙ (10 + 2) = 6 ∙ 10 + 6 ∙ 2 = 60 + 12 = 72
98 : 2 = (80 + 18) : 2 = 80 : 2 + 18 : 2 = 40 + 9 = 49
Номер 4.
Выполни действия и сделай проверку.
Ответ:27 ∙ 3 = 81 99 : 11 = 9
Проверка: Проверка
81 : 3 = 27 9 ∙ 11 = 99
27 = 27 99 = 99
4 ∙ 18 = 72 91 : 7 = 13
Проверка: Проверка:
72 : 18 = 4 13 ∙ 7 = 91
4 = 4 91 = 91
1) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
2) Чтобы разделить сумму на число можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
27 ∙ 3 = (20 + 7) ∙ 3 = 20 ∙ 3 + 7 ∙ 3 = 60 + 21 = 81
Представим число 27 в виде суммы чисел 20 и 7, каждое слагаемое умножим на 3 и полученные результаты сложим.
99 : 11 = ?
Пробуем в частном 8 и проверяем: 11 ∙ 8 = 88, 88 < 99, число 8 не подходит.
Пробуем в частном 9 и проверяем: 11 ∙ 9 = 99, 99 = 99, значит 99 : 11 = 9.
Ответ: 9.
4 ∙ 18 = 4 ∙ (10 + 8) = 4 ∙ 10 + 4 ∙ 8 = 40 + 32 = 72
Представим число 18 в виде суммы чисел 10 и 8, каждое слагаемое умножим на 4 и полученные результаты сложим.
91 : 7 = (70 + 21) : 7 = 70 : 7 + 21 : 7 = 10 + 3 = 13
Представим число 91 в виде суммы чисел 70 и 21, каждое слагаемое разделим на 7 и полученные результаты сложим.
Делаем проверку.
27 ∙ 3 = 81
Проверка:
81 : 3 = (60 + 21) : 3 = 20 + 7 = 27
27 = 27
Решение выполнено верно.
99 : 11 = 9
Проверка:
11 ∙ 9 = (10 + 1) ∙ 9 = 90 + 9 = 99
99 = 99
Решение выполнено верно.
4 ∙ 18 = 4 ∙ (10 + 8) = 4 ∙ 10 + 4 ∙ 8 = 40 + 32 = 72
Проверка:
72 : 4 = (40 + 32) : 4 = 10 + 8 = 18
18 = 18
Решение выполнено верно.
91 : 7 = (70 + 21) : 7 = 70 : 7 + 21 : 7 = 10 + 3 = 13
Проверка:
13 ∙ 7 = (10 + 3) ∙ 7 = 70 + 21 = 91
91 = 91
Решение выполнено верно.
Номер 5.
Ответ:90 : 5 > 90 : 10, потому что при одинаковых делимых частное будет больше, когда делитель меньше.
35 ∙ 1 = 35 ∙ 0 + 35
48 : 4 < 52 : 4, потому что при одинаковых делителях частное будет больше, когда делимое больше.
35 + 1 > (35 + 0) ∙ 1
Можно такое оформление выбрать:

1) Равенство – это запись, в которой есть знак равно.
2) Неравенство – это запись, в которой есть знак больше или меньше.
Рассуждаем.
90 : 5 > 90 : 10
Так как при одинаковых делимых частное будет больше, когда делитель меньше.
48 : 4 < 52 : 4
Так как при одинаковых делителях частное будет больше, когда делимое больше.
35 ∙ 1 = 35 ∙ 0 + 35
35 = 35
Если число умножить на 1, то число не изменится.
Если число умножить на 0, то произведение равно 0.
35 + 1 > (35 + 0) ∙ 1
Если к числу прибавить 1, то число увеличится на 1.
Если число умножить на 0, то произведение равно 0.
Выполним проверку.
90 : 5 > 90 : 10
90 : 5 = 18
90 : 10 = 9
18 > 9
48 : 4 < 52 : 4
48 : 4 = 12
52 : 4 = 13
12 < 13
35 ∙ 1 = 35 ∙ 0 + 35
35 ∙ 1 = 35
35 ∙ 0 + 35 = 0 ∙ 35 = 35
35 = 35
35 + 1 > (35 + 0) ∙ 1
35 + 1 = 36
(35 + 0) ∙ 1 = 35
36 > 35
Номер 6.
Путь от дома до магазина мальчик прошел за 12 мин, а от магазина до аптеки – за 18 мин. Сколько минут он затратил на весь путь от дома до аптеки?
Ответ:До магазина – 12 мин До аптеки – 18 мин Всего – ? мин 12 + 18 = 30 (мин) Ответ: мальчик затратил 30 минут.
Весь путь складывается из пути от дома до магазина и пути от магазина до аптеки.
Оформляем условие в виде схематического чертежа.
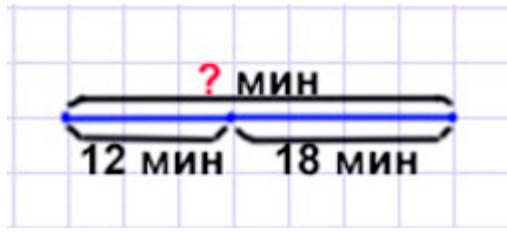
Рассуждаем.
Чтобы узнать сколько времени потратил мальчик на весь путь нужно время, которое потрачено на от дома до магазина сложить с временем от магазина до аптеки.
12 + 18 = 30 (мин.) – весь путь.
Записываем ответ.
Ответ: 30 минут.
Номер 7.
Какое самое большое число до 26 делится без остатка на 3? на 4? на 5? на 6? на 7? на 8? на 9? на 10?
Ответ:24 : 3 = 8 24 : 4 = 6 25 : 5 = 5 24 : 6 = 4 21 : 7 = 3 24 : 8 = 3 18 : 9 = 2 20 : 10 = 2
Делятся без остатка на число, значит, являются результатами таблицы умножения на это число.
Выпишем все числа до 26.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26.
Выпишем нужные числа и проверим.
24 : 3 = 8
24 : 4 = 6
25 : 5 = 5
24 : 6 = 4
21 : 7 = 3
24 : 8 = 3
18 : 9 = 2
20 : 10 = 2
Оформляем задание в тетрадь.
Самое большое число до 26 делится без остатка
на 3 – это число 24;
на 4 – это число 24;
на 5 – это число 25;
на 6 – это число 24;
на 7 – это число 21;
на 8 – это число 24;
на 9 – это число 18;
на 10 – это число 20.
Номер 8.
Ответ:45 : 15 = 3 99 : 33 = 3 80 : 16 = 5

При необходимости 2 и 3 столбики можно расписать подробнее:

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
Расставляем порядок действий и выполняем вычисления.
Вычисляем методом подбора.
45 : 15 = ?
Пробуем в частном 2 и проверяем: 15 ∙ 2 = 30, 30 < 45, число 3 не подходит.
Пробуем в частном 3 и проверяем: 15 ∙ 3 = 45, 45 = 45, значит 45 : 15 = 3.
Ответ: 3.
99 : 33 = ?
Пробуем в частном 2 и проверяем: 33 ∙ 2 = 66, 66 < 99, число 2 не подходит.
Пробуем в частном 3 и проверяем: 33 ∙ 3 = 99, 99 = 99, значит 99 : 33 = 3.
Ответ: 3.
80 : 16 = ?
Пробуем в частном 4 и проверяем: 16 ∙ 4 = 54, 54 < 80, число 4 не подходит.
Пробуем в частном 5 и проверяем: 16 ∙ 5 = 80, 80 = 80, значит 80 : 16 = 5.
Ответ: 5.
Вычисляем по действиям.
78 : 6 ∙ 3 = 39
1) 78 : 6 = (60 + 18) : 6 = 10 + 3 = 13
2) 13 ∙ 3 = (10 + 3) ∙ 3 = 30 + 9 = 39
51 : 3 ∙ 4 = 68
1) 51 : 3 = (30 + 21) : 3 = 10 + 7 = 17
2) 17 ∙ 4 = (10 + 7) ∙ 4 = 40 + 28 = 68
84 : 4 ∙ 3 = 63
1) 84 : 4 = (80 + 4) : 4 = 20 + 1 = 21
2) 21 ∙ 3 = (20 + 1) ∙ 3 = 60 + 3 = 63
100 − 4 ∙ 18 = 28
1) 4 ∙ 18 = 4 ∙ (10 + 8) = 40 + 32 = 72
2) 100 − 72 = 28
100 − 6 ∙ 13 = 22
1) 6 ∙ 13 = 6 ∙ (10 + 3) = 60 + 18 = 78
2) 100 − 78 = 22
100 − 4 ∙ 25 = 0
1) 4 ∙ 25 = 4 ∙ (20 + 5) = 80 + 20 = 100
2) 100 − 100 = 0
(34 + 36) : 10 = 7
1) 34 + 36 = 70
2) 70 : 10 = 7 дес. : 1 дес. = 7 : 1 = 7
(75 − 33) : 3 = 14
1) 75 − 33 = 42
2) 42 : 3 = (30 + 12) : 3 = 10 + 4 = 14
(82 − 16) : 33 = 2
1) 82 − 16 = 66
2) 66 : 33 = 2
Оформляем задание в тетрадь.
45 : 15 = 3, так как 15 ∙ 3 = 45
99 : 33 = 3, так как 33 ∙ 3 = 99
80 : 16 = 5, так как 16 ∙ 5 = 80
78 : 6 ∙ 3 = 13 ∙ 3 = 39
51 : 3 ∙ 4 = 17 ∙ 4 = 68
84 : 4 ∙ 3 = 21 ∙ 3 = 63
100 − 4 ∙ 18 = 100 − 72 = 28
100 − 6 ∙ 13 = 100 − 78 = 22
100 − 4 ∙ 25 = 100 − 100 = 0
(34 + 36) : 10 = 70 : 10 = 7
(75 − 33) : 3 = 42 : 3 = 14
(82 − 16) : 33 = 66 : 33 = 2
Номер 9.
От Москвы до Ставрополя поезд идет 28 ч, а самолёт тратит в 14 раз меньше времени, чем поезд. Сколько часов экономит самолёт для пассажира?
Ответ:
1) 28 : 14 = 2 (ч) – летит самолёт. 2) 28 – 2 = 26 (ч) Ответ: 26 часов экономит самолёт.
«В 14 раз меньше» – решается делением.
Оформляем условие в виде краткой записи.
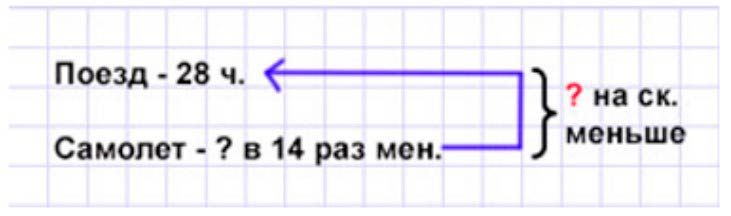
Рассуждаем.
Самолет тратит времени в 14 раз меньше, чем поезд. Значит, чтобы найти сколько времени потратит самолет от Москвы до Ставрополя, нужно время пути поезда уменьшить в 14 раз, то есть разделить на 14.
28 : 14 = 2 (ч.) – летит самолет.
Продолжаем рассуждение.
Чтобы узнать, на сколько одно число меньше другого, нужно из большего числа вычесть меньшее.
Значит, чтобы узнать, сколько часов экономит самолет, нужно из время поезда вычесть время самолета.
28 − 2 = 22 (ч.) – сколько экономит самолет для пассажира.
Записываем ответ.
Ответ: 22 часа.
Решение выражением:
28 − 28 : 14 = 2 (часа), где 28 : 14 – время самолета в пути.
Номер 10.
Определи, не вычисляя, меньшую из данных сумм.
Ответ:47 + 25 + 8 + 13.
Внимательно рассмотри выражения и сравни каждое слагаемое.
Рассуждаем.
В примере, в котором наименьшие слагаемые то и будет наименьшим.
Сравним каждое слагаемое из 2 примера с другими слагаемыми из 1 и 3 примера.
.jpg)
.jpg)
.jpg)
.jpg)
Делаем вывод.
47 + 25 + 8 + 13 – наименьшая сумма.
Задание на полях страницы
Начерти и продолжи:



1) Диаметр – отрезок, который проходит через центр и соединяет две любые точки на окружности.
2) Используй специальные приборы: циркуль и линейку.
Рассуждаем.
Рассмотрим рисунок.
Радиус каждой окружности равен 15 мм = 1 см 5 мм. Каждая следующая окружность начинается с центра предыдущей окружности.
Начертим.
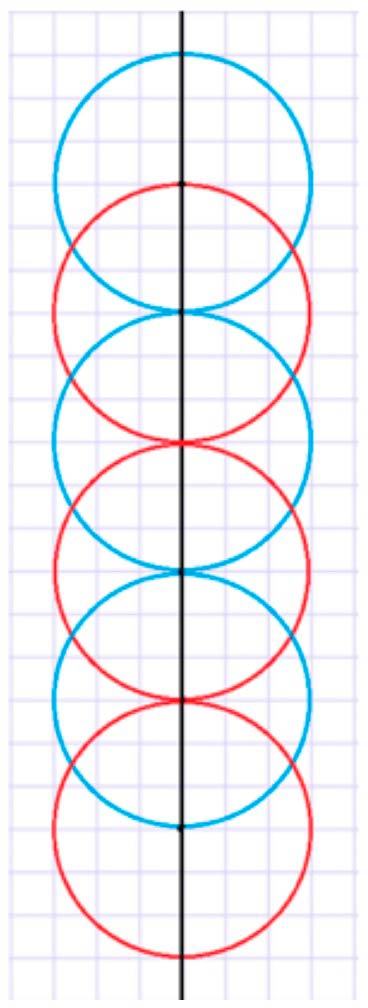
Задание внизу страницы
Странички для любознательных
Задачи-расчеты
Номер 1.
Лиза увлекается вышивкой. Часто она вышивает крестиком по канве. На этот раз она вышивает пальмы. Хватит ли ей куска канвы прямоугольной формы длиной 50 см и шириной 30 см, если клетка на канве в 4 раза больше, чем клеточка на рисунке?

Длина рисунка – 19 клеток, ширина рисунка – 36 клеток.
Сторона клетки – 2 мм.
1) 19 · 2 = (10 + 9) · 2 = 20 + 18 = 38 (мм) – длина рисунка;
2) 36 · 2 = (30 + 6) · 2 = 60 + 12 = 72 (мм) – ширина рисунка.
3) 38 · 4 = (30 + 8) · 4 = 120 + 32 = 152 (мм) – длина канвы;
4) 72 · 4 = (70 + 2) · 4 = 280 + 8 = 288 (мм) – ширина канвы.
50 см = 500 мм – длина канвы Лизы;
30 см = 300 мм – ширина канвы Лизы.
300 мм > 152 мм
500 мм > 288 мм
То есть, размеры канвы Лизы больше, чем размеры канвы, необходимые для вышивки. Значит, Лизе хватит её куска канвы.
Ответ: хватит.
1) Помни, чтобы умножить сумму на число, можно умножить на число каждое слагаемое и полученные результаты сложить.
2) Повтори меры длины – сантиметры и миллиметры.
Оформляем краткую запись.
Длина канвы – 50 см
Ширина канвы – 30 см
Клетка на канве в 4 раза больше, чем клетка на рисунке.
Хватит ли куска канвы?
Рассуждаем.
Для начала необходимо посчитать количество клеток по длине и ширине рисунка.
Длина рисунка – 19 клеток, ширина рисунка – 36 клеток.
С помощью линейки измеряем сторону клетки – 2 мм.
Продолжаем рассуждение.
Мы узнали количество клеток по длине и ширине. Теперь вычислим ширину и ширину рисунка. Для этого нужно количество клеток умножить на длину клетки.
1) 19 ∙ 2 = (10 + 9) ∙ 2 = 20 + 18 = 38 (мм) – длина рисунка;
2) 36 ∙ 2 = (30 + 6) ∙ 2 = 60 + 12 = 72 (мм) – ширина рисунка.
Продолжаем рассуждение.
Мы узнали размеры рисунка, также нам известно, что клетка на канве в 4 раза больше, чем клетка на рисунке. Значит, мы можем узнать каких размеров необходима канва. Для этого размеры рисунка умножим на 4.
1) 38 ∙ 4 = (30 + 8) ∙ 4 = 120 + 32 = 152 (мм) – длина канвы;
2) 72 ∙ 4 = (70 + 2) ∙ 4 = 280 + 8 = 288 (мм) – ширина канвы.
Сравним размеры канвы.
Нужно узнать, хватит ли Лизе куска канвы 50 см на 30 см для вышивки. Мы уже узнали, для того, чтобы вышить рисунок с пальмами, нужна канва размерами 152 мм на 288 мм.
50 см = 500 мм – длина канвы Лизы;
30 см = 300 мм – ширина канвы Лизы.
Сравним размеры.
300 мм > 152 мм
500 мм > 288 мм
То есть, размеры канвы Лизы больше, чем размеры канвы, необходимые для вышивки. Значит, Лизе хватит её куска канвы.
Записываем ответ.
Ответ: Лизе хватит куска канвы.
Номер 2.
На обивку дивана расходуют 6 м ткани, а на обивку двух кресел – 3 м. У мастера есть 24 м ткани. Может ли он обить этой тканью 3 дивана и 2 пары кресел? 1 диван и 4 пары кресел?
Ответ:1) 6 ∙ 3 + 3 ∙ 2 = 24 (м) – понадобится мастеру на обивку 3 диванов и 2 пар кресел. 2) 6 ∙ 1 + 3 ∙ 4 = 18 (м) – понадобится мастеру на обивку 1 дивана и 4 пар кресел. 3) 24 – 24 = 0 (м) – останется если обить 3 дивана и 2 пары кресел. (Хватит) 4) 24 – 18 = 6 (м) – останется если обить 1 диван и 2 пары кресел. (Хватит) Ответ: ткани хватит на обивку 3 диванов и 2 пар кресел; ткани хватит на обивку 1 дивана и 4 пар кресел.
1) Вспомни таблицу умножения.
2) Одна пара – это два одинаковых предмета.
Оформляем краткую запись.
Обивка дивана – 6 м ткани.
Обивка 1 пары кресел – 3 м ткани.
Всего – 24 м ткани.
Хватит ли ткани на 3 дивана и 2 пары кресел?
Хватит ли ткани на 1 диван и 4 пары кресел?
Рассуждаем.
Сначала необходимо узнать, сколько ткани понадобится, что обить 3 дивана и 2 пары кресел. Для этого нужно количество ткани на 1 диван умножить на количество диванов, а затем количество ткани на 1 пару кресел умножить на количество пар кресел, и полученные результаты сложить.
1) 6 ∙ 3 = 18 (м) – ткани понадобится на 3 дивана;
2) 3 ∙ 2 = 6 (м) – ткани понадобится на 2 пары кресел;
3) 18 + 6 = 24 (м) – ткани понадобится на 3 дивана и 2 пары кресел.
Продолжаем рассуждение.
Теперь точно также найдём, сколько ткани понадобится, что обить 1 диван и 4 пары кресел.
1) 3 ∙ 4 = 12 (м) – ткани понадобится на 4 пары кресел;
2) 6 + 12 = 18 (м) – ткани понадобится на 1 дивана и 4 пары кресел.
Продолжаем рассуждение.
Чтобы узнать, может ли мастер обить своей ткань мебель, нужно из общего количества ткани, которая есть у мастера, вычесть то количество ткани, которое понадобится для обивки мебели.
1) 24 – 24 = 0 (м) – останется, если обить 3 дивана и 2 пары кресел.
2) 24 – 18 = 6 (м) – останется, если обить 1 диван и 4 пары кресел.
В первом случае, у мастера уйдёт вся ткань на обивку, во втором, у него даже останется ещё 6 м ткани.
Записываем ответ.
Ответ: 24 м ткани хватит на обивку 3 диванов и 2 пар кресел или на обивку 1 дивана и 4 пар кресел.
Номер 3.
Из куска ткани можно сшить 12 пляжных зонтов, расходуя на каждый по 6 м. Можно ли сшить 9 палаток из этого куска ткани, если на одну палатку расходуют ткани на 3 м больше, чем на один зонт?
Ответ:
1) 12 ∙ 6 = 72 (м) – ткани было. 2) 6 + 3 = 9 (м) – ткани расходуется на палатку. 3) 72 : 9 = 8 (п.) – можно сшить. 4) 8 < 9 – ткани не хватает. Ответ: нельзя сшить 9 палаток.
Данная задача: вида «количество ткани на 1 предмет, количество предметов, общее количество ткани» характеризуется зависимостями между элементами:
Кол-во ткани на 1 предмет · кол-во предметов = общее кол-во ткани.
Общее кол-во ткани: кол-во ткани на 1 предмет = кол-во предметов.
Общее кол-во ткани: кол-во предметов = кол-во ткани на 1 предмет.
Оформляем краткую запись.
.jpg)
Рассуждаем.
Согласно условиям задачи, из куска ткани можно сшить 12 пляжных зонтов, расходуя на каждый по 6 м. Чтобы узнать, сколько всего м ткани в данном куске, нужно количество зонтов умножить на количество ткани, необходимой для пошива одного зонта.
12 ∙ 6 = (10 + 2) ∙ 6 = 60 + 12 = 72 (м) – ткани всего.
Продолжаем рассуждение.
Также в задаче сказано, что на одну палатку расходуют ткани на 3 м больше, чем на один зонт. Значит, можем узнать, сколько метров ткани расходуют на одну палатку. Для этого нужно к количеству ткани, необходимой для пошива одного зонта, прибавить 3м.
6 + 3 = 9 (м) – ткани расходуется на палатку.
Продолжаем рассуждение.
Мы узнали, сколько всего метров ткани есть и сколько ткани расходуется на одну палатку. Чтобы узнать, сколько палаток можно сшить из этой ткани, нужно общее количество ткани разделить на количество ткани, необходимой для пошива одной палатки.
72 : 9 = 8 (п.) – можно сшить.
8 < 9, значит, на пошив 9 палаток данного куска ткани не хватит.
Записываем ответ.
Ответ: нельзя сшить 9 палаток.
Номер 4.
Для покупки журналов «В стране знаний» мама дала Даше 100 р. Хватит ли этих денег, чтобы купить 3 выпуска этого журнала, если первый выпуск стоит 30 р., второй – 31 р., а третий – 29 р.? Сделай устно прикидку, а потом проверь вычислением.
Ответ:30 + 31 + 29 = 90 (р.) – цена покупки. Ответ: денег хватит, чтобы купить 3 выпуска этого журнала.
1) Вспомни таблицу умножения на 3.
2) Помни, что в одном десятке 10 единиц.
Оформляем краткую запись.
1 выпуск – 30 р.
2 выпуск – 31 р.
3 выпуск – 29 р.
У Даши – 100 р.
Хватит ли денег на три журнала?
Рассуждаем.
Мама дала Даше 100 рублей. Она хочет купить три журнала, каждый из которых стоит примерно 30 рублей.
100 = 10 дес.
30 = 3 дес.
Из таблицы умножения мы знаем, что 3 ∙ 3 = 9
9 < 10, следовательно, Даше должно хватит денег.
Продолжаем рассуждение.
Проверим наше предположение с помощью вычисления. Для этого сложим стоимости всех трёх выпусков журнала.
30 + 31 + 29 = 61 + 29 = 90 (р.) – стоят 3 выпуска журнала.
90 < 100, значит, Даше хватит денег на покупку журналов.
Записываем ответ.
Ответ: Даше хватит денег на покупку журналов.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.