Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 12

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 2.
- Год: 2021-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Странички для любознательных
Номер 1.
Девочке подарили кружево длиной 84 см. Она решила обшить кружевом платочек квадратной формы. Какого размера платочек она может обшить этим кружевом, если на каждый уголок нужно добавить по 1 см?
Ответ:1-й способ решения:
1) 4 ∙ 1 = 4 (см) – нужно добавить на уголки.
2) 84 – 4 = 80 (см) – периметр платочка.
3) 80 : 4 = 20 (см) – длина стороны платочка.
Ответ: девочка может обшить платочек в форме квадрата с длиной стороны 20 см.
2-й способ решения:
(84 – 1 ∙ 4) : 4 = (84 – 4) : 4 = 80 : 4 = 20 (см) – длина одной стороны платочка.
Ответ: 20 см.
1) Квадрат – это прямоугольник, у которого все стороны равны.
2) Периметр квадрата – это сумма всех его сторон.
Рассуждаем.
Чтобы обшить платочек на каждый уголок нужно по 1 см. Всего уголков 4. Чтобы узнать сколько уйдёт кружева на уголки нужно 1 см умножить на количество уголков.
1 ∙ 4 = 4 (см) – нужно добавить на уголки.
Продолжаем рассуждения.
Узнаем сколько кружева останется на периметр платочка. Для этого нужно из общей длины кружева вычесть длину кружева, которая ушла на уголки.
84 − 4 = 80 (см) — останется на платочек
Продолжаем рассуждения.
Чтобы найти периметр квадрата нужно длину стороны квадрата умножить на 4.
Значит, чтобы найти длину стороны квадрата, нужно периметр разделить на 4, так как все стороны у квадрата равны.
80 : 4 = 20 (см) — длина одной стороны платочка.
Записываем ответ.
Ответ: 20 см.
Номер 2.
Лист бумаги прямоугольной формы сложи вдвое, а потом еще раз вдвое, как показано на рисунке. Измерь стороны полученного прямоугольника и найди его периметр. Определи без измерений периметр развернутого листа.


Р = 2 ∙ 2 + 4 ∙ 2 = 12 см Периметр развернутого листа равен учетверенной сумме двух сторон полученного прямоугольника. Ответ: периметр развёрнутого листа равен учетверённой сумме двух сторон полученного прямоугольника.
Вспомни, что периметр – это сумма длин всех сторон.
Рассуждаем.
После того как лист бумаги сложили 2 раза, получился прямоугольник со сторонами 2 см и 1 см.
.jpg)
Чтобы найти периметр такого прямоугольника, нужно сложить длину и ширину прямоугольника, и полученную сумму умножить на 2.
(2 + 1) ∙ 2 = 3 ∙ 2 = 6 (см) – периметр полученного прямоугольника.
Продолжаем рассуждения.
Разогнём сложенный прямоугольник 1 раз. Получим прямоугольник (квадрат) с шириной и длиной 2 см.
.jpg)
Разогнём прямоугольник 2 раз. Получим прямоугольник с шириной и длиной 2 см и 4 см.
.jpg)
Найдём его периметр.
(2 + 4) ∙ 2 = 6 ∙ 2 = 12 (см) – периметр развёрнутого листа
Делаем вывод и оформляем задание в тетрадь.
.jpg)
Ширина и длина полученного (сложенного) прямоугольника и изначального (развернутого) прямоугольника меньше в 2 раза.
В итоге и периметр также будет в 2 раза меньше.
Значит, чтобы найти периметр разложенного листа, нужно периметр полученного (сложенного) прямоугольника умножить на 2.
6 см ∙ 2 = 12 (см) – периметр изначального листа.
Ответ: 12 см.
Номер 3.
Узнай и запиши по порядку, чему равен периметр первого, второго, третьего и четвертого прямоугольников. По полученной записи догадайся, каким будет периметр пятого прямоугольника. Проверь себя измерениями. Начерти в тетради шестой прямоугольник и найди его периметр.

Одна сторона прямоугольника остается неизменной, а вторая увеличивается на 1. Из-за этого периметр растет на 2 см.
(1 + 1) ∙ 2 = 4 см
(1 + 2) ∙ 2 = 6 см
(3 + 1) ∙ 2 = 8 см
(4 + 1) ∙ 2 = 10 см
(5 + 1) ∙ 2 = 12 см
(6 + 1) ∙ 2 = 14 см
Периметр 6 прямоугольника – 14 см.

1) Вспомни, что периметр – это сумма длин всех сторон.
2) Для того, чтобы узнать периметр шестого прямоугольника, необходимо увидеть закономерность.
Рассмотрим прямоугольники.
С помощью линейки измерим стороны прямоугольников.
Прямоугольник 1 – это квадрат со стороной 1 см;
Прямоугольник 2 – длина – 1 см; ширина - 2 см;
Прямоугольник 3 – длина – 1 см; ширина - 3 см;
Прямоугольник 4 – длина – 1 см; ширина - 4 см;
Прямоугольник 5 – длина – 1 см; ширина - 5 см.
Вычислим периметры.
Чтобы найти периметр такого прямоугольника, нужно сложить длину и ширину прямоугольника, и полученную сумму умножить на 2.
(1 + 1) ∙ 2 = 4 (см) – периметр 1 прямоугольника
(1 + 2) ∙ 2 = 6 (см) – периметр 2 прямоугольника
(1+ 3) ∙ 2 = 8 (см) – периметр 3 прямоугольника
(1 + 4) ∙ 2 = 10 (см) – периметр 4 прямоугольника
(1 + 5) ∙ 2 = 12 (см) – периметр 5 прямоугольника
Делаем вывод.
Ширина прямоугольника остаётся неизменной, а длина увеличивается на 1 см. Значит, периметр прямоугольника каждый раз увеличиваться на 2 см.
Тогда у 6 прямоугольника:
1) длина равна 1 см, а ширина – 6 см.
2) (1 + 6) ∙ 2 = 7 ∙ 2 = 14 (см) – периметр 6 прямоугольника.
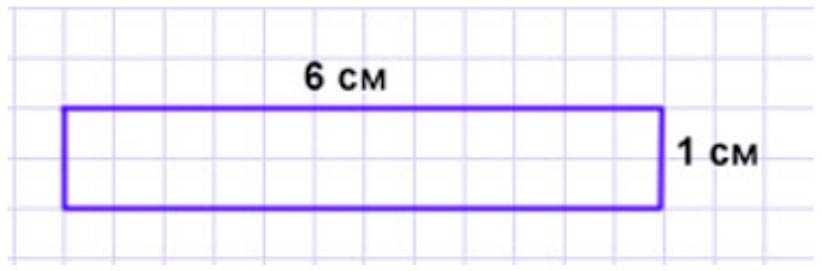
Начертим прямоугольник.
С помощью линейки начертим прямоугольник со сторонами 1 см и 6 см.
Номер 4.
Продолжи ряды чисел:
1) 51, 52, 0, 53, 54, 0, ... 2) 99, 98, 96, 95, 93, ...
Ответ:1) 55, 56, 0, 57, 58, 0 ... – закономерность такова, что называют два последовательных числа, затем ноль, снова для последовательных числа и ноль. 2) 92, 90, 89, 87, 86, 84 ... – называют число, затем одн пропускают и два последовательных. Одно число пропускают и называют два последовательных.
Для того, чтобы продолжить ряд чисел, необходимо увидеть закономерность.
Рассуждаем.
Рассмотрим 1 ряд чисел. Каждое следующее число больше на 1, но каждое третье число или через каждые 2 числа – нуль.
Рассмотрим 2 ряд чисел.
Сначала из числа вычитают 1, потом вычитают 2 и так далее.
99 − 1 = 98
98 − 2 = 96
96 − 1 = 95
95 − 2 = 93
93 − 1 = 92
92 − 2 = 90
90 − 1 = 89 и т.д.
Продолжим ряды.
1 ряд: 51, 52, 0, 53, 54, 0, 55, 56, 0, 57, 58, 0, …
2 ряд: 99, 98, 96, 95, 93, 92, 90, 89, 87, 86, 84, …
Номер 1.
Вычисли с устным объяснением.
Ответ:(80 + 16) : 4 = 80 : 4 + 16 : 4 = 20 + 4 = 24
Разделим слагаемые 80 и 16 на 4, полученные результаты сложим.
(30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
Разделим слагаемые 30 и 21 на 3, полученные результаты 7 и 10 сложим.
(11 + 13) : 6 = 24 : 6 = 4
Вычислим сумму 11 и 13 и разделим ее – 24 на 6.
1) Помни, чтобы разделить сумму на число, можно вычислить сумму и разделить её на число.
2) Помни, чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Чтобы разделить сумму на число, можно сначала вычислить сумму, а потом разделить полученный результат на число, или разделить на число каждое слагаемое и полученные результаты сложить.
(80 + 16) : 4 = 24
В данном выражении, так как 80 и 16 делится на 4, разделим каждое слагаемое и полученные результаты сложим.
80 : 4 = 20
16 : 4 = 4
20 + 4 = 24
(30 + 21) : 3 = 17
В данном выражении, так как 30 и 21 делятся на 3, разделим каждое слагаемое и полученные результаты сложим.
30 : 3 = 10
21 : 3 = 7
10 + 7 = 17
(11 + 13) : 6 = 4
В данном выражении 11 и 13 не делятся на 6, тогда сначала вычислим сумму, а затем разделим её число.
11 + 13 = 24
24 : 6 = 4
Оформляем задание в тетрадь.
(80 + 16) : 4 = 80 : 4 + 16 : 4 = 20 + 4 = 24
(30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17
(11 + 13) : 6 = 24 : 6 = 4
Номер 2.
У одной закройщицы было 15 м ткани, а у другой – 12 м. Из этой ткани они скроили платья, расходуя на каждое по 3 м ткани. Сколько всего платьев они скроили? Сколькими способами можно решить эту задачу? Какой способ выбираешь ты? Почему?
Ответ:
1-й способ решения:
1) 15 + 12 = 27 (м) – всего ткани.
2) 27 : 3 = 9 (пл.) – скроили две закройщицы всего вместе.
Ответ: 9 платьев скроили две закройщицы вместе.
2-й способ решения:
1) 15 : 3 = 5 (пл.) – скроила первая закройщица.
2) 12 : 3 = 4 (пл.) – скроила вторая закройщица.
3) 5 + 4 = 9 (пл.) – скроили две закройщицы всего вместе.
Ответ: 9 платьев скроили две закройщицы вместе.
Первый способ удобнее, так как выполняем меньше действий.
1) Помни, чтобы разделить сумму на число, можно вычислить сумму и разделить её на число.
2) Помни, чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Оформляем краткую запись в виде таблицы.
.jpg)
Задачу можно решить двумя способами.
Но удобнее всего решать первым способом, так как для решения требуется выполнить меньше действий.
Рассуждаем.
По условию задачи известно, что у одной закройщицы было 15 м ткани, а у другой – 12 м. Из этого можем узнать, сколько всего м ткани у них было.
Для этого необходимо сложить количество ткани первой и второй закройщицы.
15 + 12 = 27 (м) – ткани всего было у закройщиц.
Продолжаем рассуждение.
Мы знаем, что на одно платье расходуется 3 м ткани, а всего 27 м. Чтобы узнать, сколько платьев скроили закройщицы, нужно общее количество ткани разделить на то количество ткани, которое расходуется на одно платье.
27 : 3 = 9 (пл.) – скроили закройщицы.
Рассуждаем.
Из задачи мы знаем, что у одной закройщицы было 15 м ткани, а на одно платье уходит 3 м ткани. Чтобы узнать, сколько платьев она скроила, нужно общее количество её ткани разделить на то количество ткани, которое расходуется на одно платье.
15 : 3 = 5 (пл.) – скроила первая закройщица.
Продолжаем рассуждение.
Также мы знаем, что у другой закройщицы было 12 м ткани, и на одно платье она также расходовала 3 м ткани. Аналогичным способом мы можем узнать, сколько платьев она скроила.
12 : 3 = 4 (пл.) – скроила первая закройщица.
Продолжаем рассуждение.
В задаче нас просят узнать, сколько всего платьев скроили закройщицы. Для этого нам необходимо сложить количество платьев, которое скроила каждая закройщица.
5 + 4 = 9 (пл.) – всего скроили закройщицы.
Записываем ответ.
Ответ: 9 платьев скроили закройщицы.
Номер 3.
Составь задачу по выражению (20 + 30) : 5. Объясни разные способы ее решения.
Ответ:У первого сборщика было 20 деталей, а у второго 30 деталей. Сколько изделий они могут собрать, если на одно изделие расходуется 5 деталей.

1-й способ решения:
1) 20 + 30 = 50 (д.) – всего.
2) 50 : 5 = 10 (изд.) собрали сборщики вместе
Ответ: 10 изделий смогут собрать два сборщика вместе.
В первом способе решения сначала находим сумм всех деталей, затем делим на 5. Во втором способе делим каждое слагаемое отдельно, а результаты складываем.
2-й способ решения:
1) 20 : 5 = 4 (изд.) – может сделать первый сборщик.
2) 30 : 5 = 6 (изд.) – может сделать второй сборщик.
3) 4 + 6 = 10 (изд.) – могут сделать два сборщика вместе.
Ответ: 10 изделий они могут сделать вместе.
В первом способе решения сначала находим сумм всех деталей, затем делим на 5. Во втором способе делим каждое слагаемое отдельно, а результаты складываем.
1) Помни, чтобы разделить сумму на число, можно вычислить сумму и разделить её на число.
2) Помни, чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Составляем задачу.
Дано выражение (20 + 30) : 5. Составим по нему задачу.
У первого сборщика было 20 деталей, а у второго – 30 деталей. Сколько изделий они могут собрать, если на одно изделие расходуется 5 деталей?
Оформляем краткую запись в виде таблицы.
.jpg)
Задачу можно решить двумя способами.
Рассуждаем.
По условию задачи известно, что у первого сборщика было 20 деталей, а у второго – 30 деталей. Из этого можем узнать, сколько всего деталей у них было. Для этого необходимо сложить количество деталей первого и второго сборщика.
20 + 30 = 50 (д.) – было всего.
Продолжаем рассуждение.
Мы знаем, что на одно изделие расходуется 5 деталей, а всего 50 деталей. Чтобы узнать, сколько изделий могут собрать сборщики, нужно общее количество деталей разделить на то количество деталей, которое расходуется на одно изделие.
50 : 5 = 10 (изд.) – могут собрать сборщики.
Рассуждаем.
Из задачи мы знаем, что у одного сборщика было 20 деталей, а на одно изделие расходуется 5 деталей. Чтобы узнать, сколько изделий может собрать первый сборщик, нужно имеющееся у него количество деталей разделить на то количество деталей, которое расходуется на одно изделие.
20 : 5 = 4 (изд.) – может собрать первый сборщик.
Продолжаем рассуждение.
Также мы знаем, что у второго сборщика было 30 деталей, и на одно изделие у него также уходит 5 деталей. Аналогичным способом мы можем узнать, сколько изделий может собрать второй сборщик.
30 : 5 = 6 (изд.) – может собрать второй сборщик.
Продолжаем рассуждение.
В задаче нас просят узнать, сколько всего изделий они могут собрать. Для этого нам необходимо сложить количество изделий, которое может собрать каждый сборщик.
4 + 6 = 10 (изд.) – могут собрать сборщики.
Записываем ответ.
Ответ: 10 изделий могут собрать сборщики.
Номер 4.
1) Представь числа 60 и 75 в виде суммы двух слагаемых, каждое из которых делится на 5. 2) Представь число 56 в виде суммы двух слагаемых, каждое из которых делится на 8; на 7.
Ответ:1) число 60 в виде суммы двух слагаемых, которые делятся на 5: 20 + 40 5 + 55 10 + 50 30 + 30 25 + 35 15 + 45 Число 75 в виде суммы двух слагаемых, которые делятся на 5: 35 + 40 5 + 70 10 + 65 15 + 60 20 + 55 25 + 50 30 + 45. 2) Число 56 в виде суммы двух слагаемых, которые делятся на 8: 24 + 32 8 + 48 16 + 40 Число 56 в виде суммы двух слагаемых, которые делятся на 7: 21 + 35 7 + 49 14 + 42 28 + 28.
1) Помни, чтобы разделить сумму на число, можно вычислить сумму и разделить её на число.
2) Помни, чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Вспомним таблицу умножения на 5 и посчитаем пятёрками до 75:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75.
Так как все эти числа делятся на 5, мы используем их, чтобы представить числа 65 и 70 в виде суммы двух слагаемых.
Составим суммы.
5 + 55 = 60
10 + 50 = 60
15 + 45 = 60
20 + 40 = 60
25 + 35 = 60
30 + 30 = 60
5 + 70 = 75
10 + 65 = 75
15 + 60 = 75
20 + 55 = 75
25 + 50 = 75
30 + 45 = 75
35 + 40 = 75
Продолжаем рассуждение.
Вспомним таблицу умножения на 7 и посчитаем семёрками до 56:
7, 14, 21, 28, 35, 42, 49, 56.
Так как все эти числа делятся на 7, мы используем их, чтобы представить число 56 в виде суммы двух слагаемых.
Составим суммы.
7 + 49 = 56
14 + 42 = 56
21 + 35 = 56
28 + 28 = 56
Продолжаем рассуждение.
Вспомним таблицу умножения на 8 и посчитаем восьмёрками до 56:
8, 16, 24, 32, 40, 48, 56.
Так как все эти числа делятся на 8, мы используем их, чтобы представить число 56 в виде суммы двух слагаемых.
Составим суммы.
8 + 48 = 56
16 + 40 = 56
24 + 32 = 56
Оформляем задание в тетрадь.
1) 5 + 55 = 60
10 + 50 = 60
15 + 45 = 60
20 + 40 = 60
25 + 35 = 60
30 + 30 = 60
5 + 70 = 75
10 + 65 = 75
15 + 60 = 75
20 + 55 = 75
25 + 50 = 75
30 + 45 = 75
35 + 40 = 75
2) 7 + 49 = 56
14 + 42 = 56
21 + 35 = 56
28 + 28 = 56
8 + 48 = 56
16 + 40 = 56
24 + 32 = 56
Номер 5.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем, действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Помни о том, что в математике существуют частные случаи умножения. Один из них – умножение на единицу. При умножении любого числа на 1, получается число, которое умножали.
5) Существует еще и другие: умножение числа на 0, и 0 на любое число.
Расставляем порядок действий и вычисляем.
3 2 1
94 − (18 + 9) · 2 = 40
В данном выражении присутствуют действия вычитание, сложение и умножение, а также скобки. Вначале выполняем действие в скобках – сложение, а потом умножение и последним – вычитание.
1) 18 + 9 = 27
2) 27 ∙ 2 = 54
3) 94 − 54 = 40
3 2 1
16 + (14 + 7) · 3 = 79
В данном выражении присутствуют действия сложение и умножение, а также скобки. Вначале выполняем действие в скобках – сложение, а потом умножение и последним – сложение вне скобок.
1) 14 + 7 = 21
2) 21 ∙ 3 = 63
3) 16 + 63 = 79
2 1
45 − 90 : 3 = 15
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом – вычитание.
1) 90 : 3 = 30
2) 45 – 30 = 15
2 1
76 – 80 : 2 = 36
В данном выражении присутствуют действия вычитание и деление. Вначале выполняем действие деление, а потом – вычитание.
1) 80 : 2 = 40
2) 76 — 40 = 36
14 ∙ 3 = (10 + 4) ∙ 3 = 10 ∙ 3 + 4 ∙ 3 = 30 + 12 = 42
1) Представим число 14 в виде суммы чисел 10 и 4.
2) Каждое слагаемое умножим на 3, получим:
10 ∙ 3 = 30 и 4 ∙ 3 = 12.
Полученные произведения сложим, получим:
30 + 12 = 42.
5 ∙ 16 = 5 ∙ (10 + 6) = 5 ∙ 10 + 5 ∙ 6 = 50 + 30 = 80
1) Представим число 16 в виде суммы чисел 10 и 6.
2) Каждое слагаемое умножим на 5, получим:
10 ∙ 5 = 50 и 6 ∙ 5 = 30.
Полученные произведения сложим, получим:
50 + 30 = 80.
Применим правило умножение на 0 и 1.
12 ∙ 1 = 12
так как если любое число умножить на 1, то получится это же число.
12 ∙ 0 = 0
так как если любое число умножить на 0, то получится 0.
Оформляем задание в тетрадь.
3 2 1
94 − (18 + 9) · 2 = 94 − 27 · 2 = 94 − 54 = 40
3 2 1
16 + (14 + 7) · 3 = 16 + 21 · 3 = 16 + 63 = 79
2 1
45 − 90 : 3 = 45 − 30 = 15
2 1
76 – 80 : 2 = 76 – 40 = 36
14 ∙ 3 = (10 + 4) ∙ 3 = 10 ∙ 3 + 4 ∙ 3 = 30 + 12 = 42
5 ∙ 16 = 5 ∙ (10 + 6) = 5 ∙ 10 + 5 ∙ 6 = 50 + 30 = 80
12 ∙ 1 = 12
12 ∙ 0 = 0
Номер 6.
Как можно сделать равенства верными, не заменяя цифры на карточках? Запиши верные равенства.

28 : 4 = 7 54 : 6 = 9 или или 28 : 7 = 4 54 : 9 = 6
Внимательно рассмотри карточки и составь верные равенства (примеры).
Рассуждаем.
1) Рассмотрим первое выражение.
-(2024).jpg)
Если поменять две карточки с цифрами 4 и 2 местами, то получится верное равенство.
-(2024).jpg)
28 : 4 = 7
Также возможен второй вариант:
28 : 7 = 4
2) Рассмотрим второе выражение.
-(2024).jpg)
Если внимательно посмотреть, то карточки нужно поменять как показано на рисунке и получится верное равенство.
-(2024).jpg)
54 : 9 = 6
Также возможен второй вариант:
54 : 6 = 9
Оформляем задание в тетрадь.
1) 28 : 4 = 7
или
28 : 7 = 4
2) 54 : 9 = 6
или
54 : 6 = 9
Задание внизу страницы
Вычисли.
Ответ:
1) Помни, чтобы разделить сумму на число, можно вычислить сумму и разделить её на число.
2) Помни, чтобы разделить сумму на число, можно разделить на число каждое слагаемое и полученные результаты сложить.
Рассуждаем.
Применяем деление суммы на число - нужно разделить на число каждое слагаемое и полученные результаты сложить.
(20 + 12) : 2 = 20 : 2 + 12 : 2 = 10 + 6 = 16
Каждое слагаемое разделим на 2, получим:
20 : 2 = 10 и 12 : 2 = 6.
Полученные частные сложим, получим:
10 + 6 = 16.
Применяем деление суммы на число – нужно вычислить сумму и разделить её на число.
(23 + 25) : 8 = 48 : 8 = 6
Сложим слагаемые и получим,
23 + 25 = 48.
Полученную сумму разделим на 8, получим:
48 : 8 = 6
Оформляем задание в тетрадь.
(20 + 12) : 2 = 20 : 2 + 12 : 2 = 10 + 6 = 16
(23 + 25) : 8 = 48 : 8 = 6
Задание на полях страницы
Магические квадраты:


Магический квадрат – квадрат, в котором все числа на одной линии в сумме по горизонтали, вертикали и диагонали образуют в сумме одно и то же число.
Рассуждаем.
Чтобы узнать, какая сумма должна быть на каждой линии, сложим имеющиеся числа по диагонали.
48 + 33 + 18 = 81 + 18 = 99
Рассмотрим первый столбец.
28 + + 48 = 99
В столбце не хватает второго числа.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
99 – (28 + 48) = 99 – 76 = 23
23 – недостающее число в первом столбце.
Продолжаем рассуждения.
Рассмотрим первую строку.
28 + + 18 = 99
В строке не хватает второго числа.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известные слагаемые.
99 – (28 + 18) = 99 – 46 = 53
53 – недостающее число в первой строке.
Продолжаем рассуждения.
Рассмотрим вторую строку.
23 + 33 + = 99
В строчке не хватает третьего числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
99 – (23 + 33) = 99 – 56 = 43
43 – недостающее число во второй строке.
Продолжаем рассуждения.
Рассмотрим второй столбец.
53 + 33 + = 99
В столбце не хватает третьего числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
99 – (53 + 33) = 99 – 86 = 13
13 – недостающее число во втором столбце.
Продолжаем рассуждения.
Рассмотрим третий столбец.
18 + 43 + = 99
В столбце не хватает третьего числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
99 – (18 + 43) = 99 – 61 = 38
38 – недостающее число в третьем столбце.
Рассуждаем.
Чтобы узнать, какая сумма должна быть на каждой линии, сложим имеющиеся числа в третьей строке.
39 + 18 + 33 = 57 + 33 = 90
Рассмотрим третий столбец.
21 + + 33 = 90
В столбце не хватает второго числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
90 – (21 + 33) = 90 – 54 = 36
36 – недостающее число в третьем столбце.
Продолжаем рассуждения.
Рассмотрим диагональ.
39 + + 21 = 90
На диагонали не хватает второго числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
90 – (39 + 21) = 90 – 60 = 30
30 – недостающее число на диагонали.
Продолжаем рассуждения.
Рассмотрим вторую строку.
+ 30 + 36 = 90
В строчке не хватает первого числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
90 – (30 + 36) = 90 – 66 = 24
24 – недостающее число во второй строке.
Продолжаем рассуждения.
Рассмотрим второй столбец.
+ 30 + 18 = 90
В столбце не хватает первого числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
90 – (30 + 18) = 90 – 48 = 42
42 – недостающее число во втором столбце.
Продолжаем рассуждения.
Рассмотрим первый столбец.
+ 24 + 39 = 90
В столбце не хватает первого числа.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известные слагаемые.
90 – (24 + 39) = 90 – 63 = 27
27 – недостающее число в первом столбце.
Запишем недостающие числа в квадрат.
.jpg)
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.