Математика 3 класс учебник Моро, Волкова 2 часть ответы – страница 11

Шаг 1.
Прочитаем выражения.

a + b – сумма a и b;
a – первое слагаемое; b – второе слагаемое

c – d – разность c и d.
c – уменьшаемое; d – вычитаемое.

Шаг 2.
Рассуждаем.

Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число.

Если а = 58 и b = 26, то a + b = 58 + 26 = 84
Если с = 53 и d = 16, то c − d = 53 – 16 = 37

Шаг 1.
Рассуждаем.

c + d, значит, к значению c нужно прибавить значение d.
m − n, значит, из значения m нужно вычесть значение n.

Шаг 2.
Вычислим.

Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число.

с + d, если
с = 48 и d = 12, то 48 + 12 = 60
с = 30 и d = 43, то 30 + 43 = 73
с = 1 и d = 89, то 1 + 89 = 90
с = 24 и d = 6, то 24 + 6 = 30

m − n, если
m = 80 и n = 35, то 80 − 35 = 45
m = 100 и n = 7, то 100 − 7 = 93
m = 21 и n = 9, то 21 − 9 = 12
m = 64 и n = 50, то 64 − 50 = 14

Шаг 1.
Рассуждаем и расставляем порядок действий.

  1      2
6 · 11 + 6 = 72
В данном выражении присутствуют действия сложение и умножение. Вначале выполняем действие умножение, а потом - сложение.

  1      2
9 · 11 − 97 = 2
В данном выражении присутствуют действия вычитание и умножение. Вначале выполняем действие умножение, а потом – вычитание.

  1    3    2
8 · 8 − 4 · 7 = 36
В данном выражении присутствуют действия вычитание и умножения. Вначале выполняем действия умножения по порядку слева направо, а потом – вычитание.

   2    1
7 + 3 · 9 = 34
В данном выражении присутствуют действия сложение и умножение. Вначале выполняем действие умножение, а потом – сложение.

     1       2
24 + 60 − 83 = 1
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполняем вычисления по порядку слева направо.

    1        2
86 − 16 + 25 = 95
В данном выражении присутствуют действия сложение и вычитание – они равносильны. Выполняем вычисления по порядку слева направо.

Шаг 2.
Выполняем вычисления по действиям.

  1      2
6 · 11 + 6 = 72
1) 6 ∙ 11 = 66
2) 66 + 6 = 72

  1      2
9 · 11 − 97 = 2
1) 9 ∙ 11 = 99
2) 99 − 97 = 2

  1    3    2
8 · 8 − 4 · 7 = 36
1) 8 ∙ 8 = 64
2) 4 ∙ 7 = 28
3) 64 − 28 = 36

   2    1
7 + 3 · 9 = 34
1) 3 ∙ 9 = 27
2) 7 + 27 = 34

     1       2
24 + 60 − 83 = 1
1) 24 + 60 = 84
2) 84 − 83 = 1

    1        2
86 − 16 + 25 = 95
1) 80 − 16 = 70
2) 70 + 25 = 95

Шаг 3.
Оформляем задание в тетрадь.

  1      2
6 · 11 + 6 = 66 + 6 = 72

  1      2
9 · 11 − 97 = 99 − 97 = 2

  1    3    2
8 · 8 − 4 · 7 = 64 − 28 = 36

   2    1
7 + 3 · 9 = 7 + 27 = 34

     1       2
24 + 60 − 83 = 84 − 83 = 1

    1        2
86 − 16 + 25 = 70 + 25 = 95

Шаг 1.
Оформляем условие в виде краткой записи.

Шаг 2.
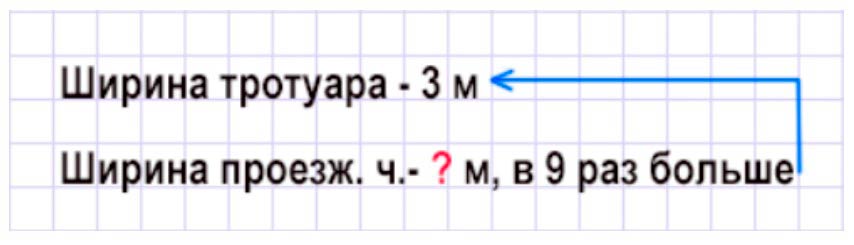
Рассуждаем.

Рассмотрим первое выражение – 3 ∙ 9

Ширину тротуара умножили на 9, то есть увеличили в 9 раз. Также по условию, мы знаем, что ширина проезжей части в 9 раз больше, чем тротуара. Значит, данным выражением мы найдём ширину проезжей части.

3 ∙ 9 = 27 (м) – ширина проезжей части.

Шаг 3.
Продолжаем рассуждения.

Рассмотрим второе выражение – 3 ∙ 2

Ширину тротуара умножили на 2. Значит, мы найдём ширину двух тротуаров.

3 ∙ 2 = 6 (м) – ширина 2 тротуаров.

Шаг 4.
Продолжаем рассуждения.

Рассмотрим третье выражение – 3 ∙ 9 + 3 ∙ 2

Ширина проезжей части складывается с шириной двух тротуаров или это ширина дороги.

3 ∙ 9 + 3 ∙ 2 = 27 + 6 = 33 (м) – ширина 2 тротуаров и проезжей части или ширина всей дороги.

Шаг 5.
Оформляем задание в тетрадь.

3 ∙ 9 = 27 (м) – ширина проезжей части
3 ∙ 2 = 6 (м) – ширина 2 тротуаров
3 ∙ 9 + 3 ∙ 2 = 27 + 6 = 33 (м) – ширина 2 тротуаров и проезжей части или ширина всей дороги.

Шаг 1.
Оформляем условие в виде схемы.

Шаг 2.
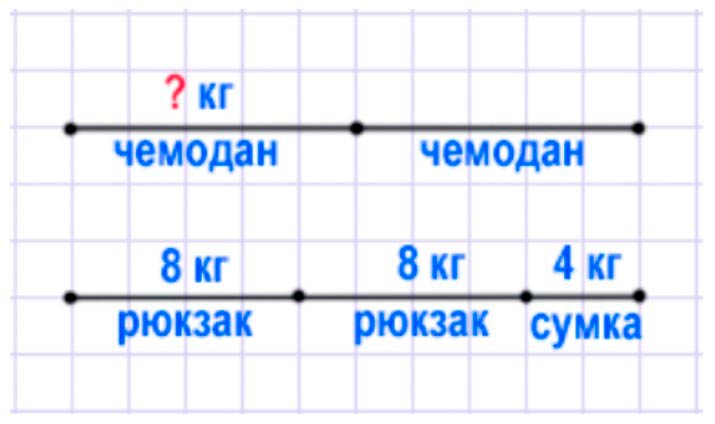
Рассуждаем.

Мы знаем, что 2 Чемодана = 2 Рюкзака + Сумка

Для начала найдём массу двух одинаковых рюкзаков. Это значит массу рюкзака нужно умножить на 2.

8 ∙ 2 = 16 (кг) – масса 2 рюкзаков.

Шаг 3.
Продолжаем рассуждения.

Теперь найдём массу двух рюкзаков и сумки. Значит, нужно к массе двух рюкзаков прибавить массу сумки.

16 + 4 = 20 (кг) – масса 2 рюкзаков и сумки или масса 2 чемоданов.

Шаг 4.
Продолжаем рассуждения.

Мы нашли массу двух рюкзаков и сумки, также мы знаем, что эта масса равна массе двух чемоданов. Значит, масса двух одинаковых чемоданов равна 16 кг.
Чемоданы одинаковы, значит, чтобы узнать массу одного такого чемодана, нужно общую массу разделить на 2.

20 : 2 = 10 (кг) – масса 1 чемодана.

Шаг 5.
Оформляем задание в тетрадь.

1) 8 ∙ 2 = 16 (кг) – масса 2 рюкзаков
2) 16 + 4 = 20 (кг) – масса 2 рюкзаков и сумка или масса 2 чемоданов
3) 20 : 2 = 10 (кг) – масса 1 чемодана

Ответ: 10 кг.

Шаг 1.
Рассуждаем.

c ∙ d, значит, значение c нужно умножить на d

Шаг 2.
Вычисляем.

Чтобы найти значение буквенного выражения, нужно вместо неизвестной буквы подставить данное число.

с ∙ d, если
с = 6 и d = 14, то
6 ∙ 14 = 6 ∙ (10 + 4) = 6 ∙ 10 + 6 ∙ 4 = 60 + 24 = 84.
Представим 14 в виде суммы чисел 10 и 4, умножим каждое слагаемое на 6 и полученные результаты сложим.

с = 24 и d = 4, то
24 ∙ 4 = (20 + 4) ∙ 4 = 20 ∙ 4 + 4 ∙ 4 = 80 + 16 = 96
Представим 24 в виде суммы чисел 20 и 4, умножим каждое слагаемое на 4 и полученные результаты сложим.

Шаг 3.
Оформляем задание в тетрадь.

с ∙ d, если
с = 6 и d = 14, то 6 ∙ 14 = 6 ∙ (10 + 4) = 60 + 24 = 84.

с = 24 и d = 4, то 24 ∙ 4 = (20 + 4) ∙ 4 = 80 + 16 = 96

Шаг 1.
Устные рассуждения.

Нужно подобрать из лабиринта числа так, чтобы при умножении и делении на них, получилось число 9.
Для этого тебе поможет таблица умножения на 9.

Шаг 2.
Записываем выражения.

6 ∙ 3 : 2 = 18 : 2 = 9
27 ∙ 2 : 6 = 54 : 6 = 9
36 ∙ 1 : 4 = 16 : 4 = 9
1 ∙ 18 : 2 = 18 : 2 = 9
18 ∙ 2 : 4 = 36 : 4 = 9
18 ∙ 3 : 6 = 54 : 6 = 9
18 ∙ 4 : 8 = 72 : 8 = 9
36 ∙ 2 : 8 = 72 : 8 = 9