Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 53

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 8.
Составь равенства, используя выражения.
Ответ:
1) Прежде, чем составить равенства, вычисли значения всех выражений.
2) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6
Вычислим значения выражений.
3 · 4 = 12
где 3 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
4 · 6= 24
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
2 · 6 = 12
где 2 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
3 · 2 = 6
где 3 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
3 · 8 = 24
где 3 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
24 : 4 = 6
так как 4 · 6 = 24
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
Составим равенства и сделаем проверку.
В равенствах правая и левая часть должны быть равны.
3 ∙ 4 = 2 ∙ 6
Проверка:
3 ∙ 4 = 12
2 ∙ 6 = 12
12 = 12
4 ∙ 6 = 3 ∙ 8
Проверка:
4 ∙ 6 = 24
3 ∙ 8 = 24
24 = 24
3 ∙ 2 = 24 : 4
Проверка:
3 ∙ 2 = 6
24 : 4 = 6
6 = 6
Оформляем задание в тетрадь.
12 12
3 ∙ 4 = 2 ∙ 6
24 24
4 ∙ 6 = 3 ∙ 8
6 6
3 ∙ 2 = 24 : 4
Номер 9.
Ответ:
3 ∙ 8 + 3 = 3 ∙ 9 7 см 8 мм < 87 мм
27 = 27 78 мм < 87 мм
4 ∙ 9 ‒ 9 < 4 ∙ 8 4 дм 5 см < 54 см
27 < 32 45 см < 54 см
1) Прежде, чем сравнить выражения, вычисли их значения в левой и правой части.
2) Помни о том, что сравнивать численных значения длины можно только, если они выражены в одних единицах измерения.
Рассмотрим выражения.
Сравним 3 · 8 + 3 и 3 · 9
Вычислим левую часть 3 · 8 + 3 – это восемь раз по 3 и еще 3, значит, это девять раз по 3. Получается, 3 · 9 = 27, где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Вычислим правую часть 3 · 9 = 27, это девять раз по 3, где 3 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Сравним 27 = 27
Значит, 3 · 8 + 3 = 3 · 9
Ставим знак равно.
Сравним 4 · 9 – 9 и 4 · 8
Вычислим левую часть 4 · 9 – 9 – это четыре раза по 9, но без одного 9, значит, это восемь раз по 4. Получается, 4 · 8 = 32, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Вычислим правую часть 4 · 8 = 32, это по 4 – 8 раз, где 4 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Сравним 32 = 32
Значит, 4 · 9 – 4 = 4 · 8
Ставим знак равно.
Сравним 7 см 8 мм и 87 мм
Вычислим левую часть 7 см 8 мм – это 70 мм и еще 8 мм – это 78 мм
Сравним 78 мм < 87 мм
Значит, 7 см 8 мм < 87 мм
Ставим знак меньше.
Сравним 4 дм 5 см и 54 см
Вычислим левую часть 4 дм 5 см – это 40 см да еще 5 см – это 45 см
Сравним 45 см < 54 см
Значит, 4 дм 5 см < 54 см
Ставим знак меньше.
Оформляем задание в тетрадь.
3 ∙ 8 + 3 = 3 ∙ 9
так как 27 = 27
4 ∙ 9 ‒ 9 < 4 ∙ 8
так как 27 < 32
7 см 8 мм < 87 мм
так как 78 мм < 87 мм
4 дм 5 см < 54 см
так как 45 см < 54 см
Номер 10.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6, 7.
Рассмотрим выражения.
7 + 21 : (15 – 8)
В выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – сложение.
50 – 24 : (11 – 5)
В выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – вычитание.
30 + 9 · (14 – 7)
В выражении присутствуют действия сложение, вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, потом умножение и последним действием – сложение.
60 – (24 + 3) : 3
В выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием – вычитание.
90 – (28 + 4) : 4
В выражении присутствуют действия сложение, вычитание и деление, а также скобки. Вначале выполняем действие в скобках – сложение, потом деление и последним действием – вычитание.
70 – (56 – 7) : 7
В выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполняем действие в скобках – вычитание, потом деление и последним действием – вычитание.
10 · 2 : 5
В выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку справа налево.
30 : 10 · 7
В выражении присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку справа налево.
40 : 10 : 4
В выражении присутствуют действия деления, поэтому выполняем действия по порядку справа налево.
Расставляем порядок действий и выполняем вычисления.
3 2 1
7 + 21 : (15 – 8) = 10
1) 15 – 8 = 7
2) 21 : 7 = 3
3) 7 + 3 = 10
3 2 1
50 – 24 : (11 – 5) = 46
1) 11 – 5 = 6
2) 24 : 6 = 4
3) 50 − 4 = 46
3 2 1
50 + 9 · (14 − 7) = 93
1) 14 – 7 = 7
2) 9 ∙ 7 = 63
3) 30 + 63 = 93
3 1 2
60 – (24 + 3) : 3 = 51
1) 24 + 3 = 27
2) 27 : 3 = 9
3) 60 − 9 = 51
3 1 2
90 − (28 + 4) : 4 = 82
1) 28 + 4 = 32
2) 32 : 4 = 8
3) 90 − 8 = 82
3 1 2
70 − (56 − 7) : 7 = 63
1) 56 – 7 = 49
2) 49 : 7 = 7
3) 70 − 7 = 63
1 2
30 : 10 ∙ 7 = 21
1) 10 ∙ 2 = 20
2) 20 : 5 = 4
1 2
30 : 10 ∙ 7 = 21
1) 30 : 10 = 3
2) 3 ∙ 7 = 21
1 2
40 : 10 : 4 = 1
1) 40 : 10 = 4
2) 4 : 4 = 1
Оформляем задание в тетрадь.
7 + 21 : (15 − 8) = 7 + 21 : 7 = 7 + 3 = 10
50 − 24 : (11 − 5) = 50 – 24 : 6 = 50 – 4 = 46
30 + 9 ∙ (14 − 7) = 30 + 9 · 7 = 30 + 63 = 93
60 − (24 + 3) : 3 = 60 – 27 : 3 = 60 – 9 = 51
90 − (28 + 4) : 4 = 90 – 32 : 4 = 90 - 8 = 82
70 − (56 − 7) : 7 = 70 – 49 : 7 = 70 – 7 = 63
10 ∙ 2 : 5 = 20 : 5 = 4
30 : 10 ∙ 7 = 3 · 7 = 21
40 : 10 : 4 = 4 : 4 = 1
Номер 11.
Реши уравнения.
Ответ:
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия деления и вычитания.
Рассмотрим уравнения.
х : 5 = 10
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
х : 7 = 6
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
28 – х = 28
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
72 – х = 7
х – неизвестное вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности.
х – 15 = 0
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
х – 48 = 7
х – неизвестное уменьшаемое.
Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
Решаем уравнение.
x : 5 = 10
x = 10 ∙ 5
x = 50
x : 7 = 6
x = 6 ∙ 7
x = 42
28 − x = 28
x = 28 − 28
x = 0
72 − x = 7
x = 72 − 7
x = 65
x − 15 = 0
x = 0 + 15
x = 15
x − 48 = 7
x = 7 + 48
x = 55
Делаем проверку.
x : 5 = 10
Проверка: вместо неизвестного подставим число 50.
50 : 5 = 10, так как 5 · 10 = 50
10 = 10 – верно.
x : 7 = 6
Проверка: вместо неизвестного подставим число 42.
42 : 7 = 6, так как 6 · 7 = 42
6 = 6 – верно.
28 − x = 28
Проверка: вместо неизвестного подставим число 0.
28 – 0 = 28
Если из числа выесть нуль, то число не изменится.
28 = 28 – верно.
72 − x = 7
Проверка: вместо неизвестного подставим число 65.
72 – 65 = 72 – (62 + 3) = (72 – 62) – 3 = 10 – 3 = 7
7 = 7 – верно.
x − 15 = 0
Проверка: вместо неизвестного подставим число 15.
15 – 15 = 0
Из числа вычесть само число, то получиться нуль.
x − 48 = 7
Проверка: вместо неизвестного подставим число 55.
55 – 48 = 55 – (45 + 3) = (55 – 45) – 3 = 10 – 3 = 7
7 = 7 – верно.
Номер 12.
(Устно.) В куске 20 м ткани. На каждый костюм расходуют по 3 м такой ткани. Можно ли из этого куска сшить 6 костюмов? 7 костюмов?
Ответ:1) 3 ∙ 6 = 18 (м) – ткани на 6 костюмов. 2) 3 ∙ 7 = 21 (м) – ткани на 7 костюмов. Ответ: можно сшить 6 костюмов, а 7 костюмов нет.
Данная задача: вида «расход на 1 костюм, количество костюм, общий расход» характеризуется зависимостями между компонентами:
Расход 1 костюма · количество костюмов = общий расход.
Общий расход : количество костюмов = расход на 1 костюм.
Общий расход : расход на 1 костюм = количество костюмов.
Оформляем условие в виде таблицы.
Общий расход ткани – 20 метров, а расход на 1 костюм – 3 м. Необходимо сшить 6 костюмов. Проверяю, хватит ли ткани на пошив 6 костюмов. Заполним таблицу данными.

Рассуждаем.
Количество костюмов – 6, а расход на 1 костюм – 3 метра. Чтобы узнать, сколько ткани израсходую на пошив 6 костюмов, нужно сложить количество ткани на каждый костюм.
Но расход ткани на каждый костюм одинаковый, значит, что сложением одинаковых слагаемых можно заменить умножением.
3 · 6 = 18 (м.) - ткани на 6 костюмов.
Продолжаем рассуждение.
Сравниваем количество ткани в куске и расход на 6 костюмов:
18 м < 20 м
Значит, количества ткани в куске хватит на пошив 6 костюмов.
Записываем ответ.
Ответ: ткани хватит на пошив 6 костюмов.
Оформляем условие в виде таблицы.
Общий расход ткани – 20 метров, а расход на 1 костюм – 3 м. Необходимо сшить 7 костюмов. Проверяю, хватит ли ткани на пошив 7 костюмов. Заполним таблицу данными.

Рассуждаем.
Количество костюмов – 7, а расход на 1 костюм – 3 метра. Чтобы узнать, сколько ткани израсходую на пошив 7 костюмов, нужно сложить количество ткани на каждый костюм.
Но расход ткани на каждый костюм одинаковый, значит, что сложением одинаковых слагаемых можно заменить умножением.
3 · 7 = 21 (м.) – ткани на 7 костюмов.
Продолжаем рассуждение.
Сравниваем количество ткани в куске и расход на 6 костюмов:
21 м > 20 м
Значит, количества ткани в куске не хватит на пошив 7 костюмов.
Записываем ответ.
Ответ: ткани не хватит на пошив 7 костюмов.
Оформляем условие в виде таблицы.
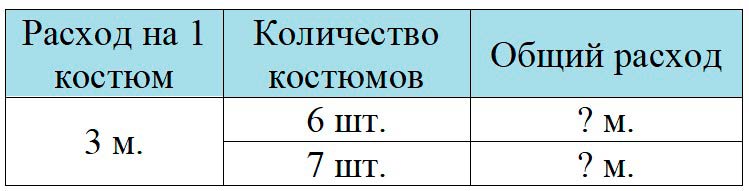
Запишем решение.
1) 3 ∙ 6 = 18 (м) − ткани на 6 костюмов.
18 < 20
20 м ткани хватит для пошива 6 костюмов.
2) 3 ∙ 7 = 21 (м) − ткани на 7 костюмов.
21 > 20
20 м ткани не хватит для пошива 7 костюмов, не хватает 1 метра ткани.
Записываем ответ.
Ответ: на 6 костюмов ткани хватит, а на 7 костбмов не хватит.
Номер 13.
Масса ящика с яблоками и трех одинаковых ящиков с виноградом равна 45 кг. Чему равна масса ящика с виноградом, если масса ящика с яблоками равна 15 кг?
Ответ:
Всего – 45 кг
Яблоки – 15 кг
Виноград – 3 ящ. по ? кг
1-й способ решения:
1) 45 − 15 = 30 (кг) – ящики с виноградом.
2) 30 : 3 = 10 (кг)
Ответ: 10 кг масса ящика винограда.
2-й способ решения: (45 – 15) : 3 = 30 : 3 = 10 (кг) – масса 1 ящика винограда. Ответ: 10 кг.
текст
Оформляем условие в виде краткой записи или таблицы.
Краткая запись:

Таблица:
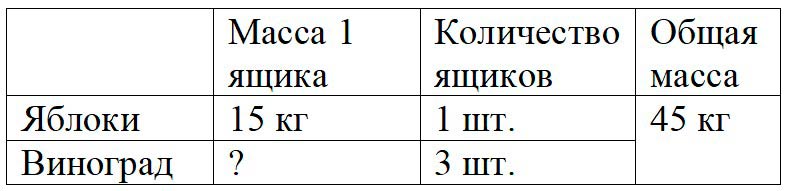
Рассуждаем.
Общая масса ящика с яблоками и трех ящиков с виноградов равна 45 кг. Она складывается из массы ящиков с яблоками и ящиков с виноградом. Соответственно, чтобы узнать, какова масса трех ящиков с виноградом, нужно из общей массы ящиков вычесть массу ящика с яблоками.
45 − 15 = 30 (кг) – масса 3 ящика с виноградом.
Продолжаем рассуждение.
Получается, 3 ящика весят 30 кг. Причем ящики одинаковые. А общая масса трех ящиков складывается из массы каждого из них. Получается, чтобы узнать, сколько весит один ящик, нужно общую массу ящиков разделить на количество ящиков.
30 : 3 = 10 (кг) – масса 1 ящик винограда.
Записываем ответ.
Ответ: масса одного ящика с виноградом 10 кг.
Решение выражением:
(45 – 15) : 3 = 10 (кг)
Номер 14.
Купили 36 цветных карандашей. Из них 12 карандашей были в большой коробке, а остальные – в маленьких коробках, по 6 штук в каждой. Сколько было маленьких коробок с карандашами?
Ответ:
Всего – 36 шт.
Большая – 12 шт.
Маленькая – ? к. по 6 шт.
1-й способ решения:
1) 36 − 12 = 24 (шт.) – в маленьких коробках.
2) 24 : 6 = 4 (к.)
Ответ: 4 маленькие коробки с карандашами было.
2-й способ решения: (36 – 12) : 6 = 24 : 6 = 4 (кор.) – было маленькими. Ответ: 4 маленьких коробки.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие в виде краткой записи или таблицы.
Краткая запись:
Краткая запись:

Таблица:
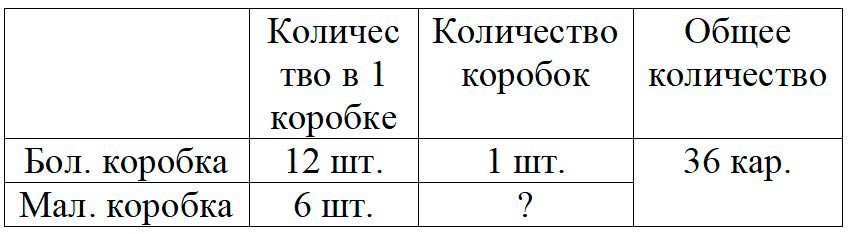
Рассуждаем.
Общее количество карандашей складывается из количества карандашей большой и маленькой коробки. Значит, чтобы узнать, сколько карандашей было в маленьких коробках, нужно из общего количества карандашей вычесть количество карандашей большой коробки.
36 − 12 = 24 (кар.) – в маленьких коробках.
Продолжаем рассуждение.
Маленьких карандашей было 24. Их разложили по 6 штук в коробки. Неизвестно количество коробок. Общее количество карандашей складывается из количества карандашей всех маленьких коробок. Значит, чтобы узнать, сколько было коробок, нужно общее количество карандашей разделить на количество карандашей одной коробки.
24 : 6 = 4 (кор.) – было маленькими.
Записываем ответ.
Ответ: 4 маленьких коробки.
Решение выражением:
(36 – 12) : 6 = 4 (кор.)
Номер 15.
Найди периметр квадрата, длина стороны которого 6 см.
Ответ:1-й способ решения: У квадрата 4 одинаковых стороны, поэтому чтобы найти его периметр нужно длину одной стороны умножить на 4. 4 ∙ 6 = 24 (см) – периметр квадрата. Ответ: 24 см.
2-й способ решения: а = 6 см Р = ? см Р = а * 4 Р = 6 ∙ 4 = 24 см Ответ: периметр квадрата равен 24 см.
Периметр – это сумма длин всех сторон.
Оформляем условие в виде таблицы.

Рассуждаем.
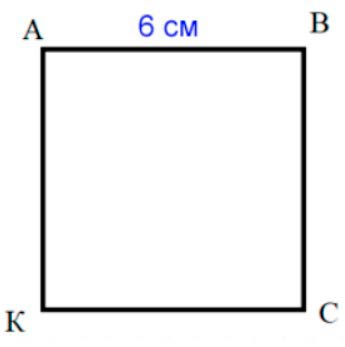
Квадрат – замкнутая ломаная. Длина ломаной равна сумме длин всех отрезков-звеньев, значит, длина квадрата – сумма длин всех его сторон.
Получается, чтобы узнать, каков периметр квадрата, нужно сложить длины всех его сторон.
Но у квадрата все стороны равны. Значит, сложение одинаковых слагаемых можно заменить умножением. поэтому, чтобы вычислить периметр квадрата, нужно длину стороны квадрата умножить на их количество.
Вычисляем периметр.
6 + 6 + 6 + 6 = 6 · 4 = 24 (см) – периметр квадрата.
Записываем ответ.
Ответ: периметр квадрата 24 см.
Номер 16.
В цирке выступали обезьянки на двух- и трехколесных велосипедах. Сколько было двух- и трехколесных велосипедов, если всего было 8 велосипедов и 21 колесо?
Ответ:1-й способ решения: 1) 8 ∙ 2 = 16 (колёс) - если все велосипеды двухколесные. 2) 21 - 16 = 5 (колёс) - лишние, значит они от трехколесных велосипедов. 3) 8 - 5 = 3 (велосипеда) - двухколесные. Ответ: 3 двухколёсных и 5 трёхколёсных велосипеда было на выступлении в цирке.
2-й способ решения:
Всего 8 велосипедов.
1) Пусть двухколесных – 1 велосипед, а трехколесных – 7 велосипедов.
Проверка: 1 ∙ 2 + 7 ∙ 3 = 2 + 21 = 23 – не подходит.
2) Пусть двухколесных – 2 велосипед, а трехколесных – 6 велосипедов.
Проверка: 2 ∙ 2 + 6 ∙ 3 = 4 + 18 = 2 – не подходит.
3) Пусть двухколесных – 3 велосипед, а трехколесных – 5 велосипедов.
Проверка: 3 ∙ 2 + 5 ∙ 3 = 6 + 15 = 21 – подходит.
Ответ: было 5 трехколесных и 3 трехколесных.
Чтобы решить задачу, нужно подобрать такую комбинацию велосипедов, чтобы количество велосипедов могло соответствовать количеству колёс.
Рассуждаем.
Предположим, что двухколесных – 1 велосипед, тогда трехколесных – 7 велосипедов.
Проверим:
1) 2 · 1 = 2 (к.) – у одного двухколёсного велосипеда.
2) 3 · 7 = 21 (к.) – у семи трёхколёсных велосипедов.
3) 2 + 21 = 23 (к.) – всего.
23 > 21 – не подходит.
Продолжаем рассуждение.
Предположим, что двухколесных – 2 велосипеда, тогда трехколесных – 6 велосипедов.
Проверим:
1) 2 · 2 = 4 (к.) – у двух двухколёсных велосипедов.
2) 3 · 6 = 18 (к.) – у шести трёхколёсных велосипедов.
3) 4 + 18 = 22 (к.) – всего.
22 > 21 – не подходит.
Продолжаем рассуждение.
Предположим, что двухколесных – 3 велосипеда, тогда трехколесных – 5 велосипедов.
Проверим:
1) 2 · 3 = 6 (к.) – у трёх двухколёсных велосипедов.
2) 3 · 5 = 15 (к.) – у пяти трёхколёсных велосипедов.
3) 6 + 15 = 21 (к.) – всего.
21 = 21 – подходит.
Записываем ответ.
Ответ: 5 – велосипедов трехколесные и 3 – велосипедов двухколесные.
Рассуждаем.
Представим, что все велосипеды двухколёсные. Всего велосипедов 8. Поэтому, чтобы узнать сколько всего колёс нужно количество велосипедов умножить на количество колёс.
8 ∙ 2 = 16 (колес) – у 8 велосипедов, если бы они были все двухколесными.
Продолжаем рассуждение.
Мы знаем, что всего 21 колесо у двухколёсных и трёхколёсных велосипедов. Узнаем сколько колёс останется, если все бы велосипеды были двухколёсными.
21 − 16 = 5 (колес) − осталось неиспользованными.
Значит эти колёса относятся к трехколесным велосипедам.
В итоге трехколесных велосипедов − 5.
Продолжаем рассуждение.
Общее велосипедов складывается из количества двухколесных велосипедов и трехколесных велосипедов. Соответственно, чтобы узнать, сколько всего двухколесных велосипедов, нужно из общего количества велосипедов вычесть количество трехколесных велосипедов.
8 − 5 = 3 (велосипеда) − двухколесных.
Проверяем решение.
5 трехколесных велосипедов и 3 двухколесных.
3 · 5 = 15 (колёс) – у трёхколёсных велосипедов.
2 · 3 = 6 (колёс) – у двух колёсных велосипедов.
15 + 6 = 21 (колесо) – всего.
21 = 21 – верно.
Записываем ответ.
Ответ: 5 – велосипедов трехколесные и 3 – велосипедов двухколесные.
Задание на полях страницы
Какая фигура лишняя?

Ответ:
1) Лишняя фигура третья сверху – треугольник, так как остальные фигуры состоят из круга и квадрата. 2) Лишняя фигура вторая сверху – круг, потому что внутри других фигур находятся круги, а в этой – квадрат.
1) Чтобы понять, какая фигура лишняя, рассмотри все.
2) Сравним их, из каких элементов они состоят.
Рассмотрим фигуры.
.jpg)
Делаем вывод.
Лишними могут быть две фигуры:
1) Лишняя фигура 2, так как так как у неё внутренняя фигура не круг, как в остальных, а квадрат.
.jpg)
2) Лишняя фигура 3, так как это единственная фигура в которой есть треугольник.
.jpg)
Номер 1.
На рисунке изображены фигуры, которые при наложении не совпадут. Докажи, что их площади равны.

Все фигуры состоят из 4 квадратов одинаковой площади, значит площади фигур равны.
Фигуры называются равными, если они при наложении совпадают. Тогда их площади равны. В противном случае равны могут быть только площади, а при наложении фигуры не совпадут.
Рассмотрим фигуры.
Жёлтая фигура состоит из 4 одинаковых квадратов.
Зелёная фигура состоит из 4 одинаковых квадратов.
Розовая фигура состоит из 4 одинаковых квадратов.
Голубая фигура состоит из 4 одинаковых квадратов.
Сравним площади фигур.
Фигуры не равные, так как не совпадут при наложении. Но они имеют одинаковое количество квадратов, поэтому их площади равны.
Номер 2.
7 · 8 49 : 7
6 · 7 63 : 9
7 · 5 42 : 6
6 · 5 - 12 45 : (18 - 13)
52 - 3 · 9 (27 + 27) :9
8 · 4 - 15 24 : (11 - 7)
7 ∙ 8 = 56 49 : 7 = 7
6 ∙ 7 = 42 63 : 9 = 7
7 ∙ 5 = 35 42 : 6 = 7

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 4, 5, 6, 7.
Выполняем умножение.
7 · 8 = 56,
где 7 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
7 · 5 = 35,
где 7 – одинаковое слагаемое, а 5 – количество одинаковых слагаемых.
Выполняем деление.
49 : 7 = 7,
так как 7 · 7 = 49,
где 7 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
63 : 9 = 7,
так как 7 · 9 = 63,
где 7 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
42 : 6 = 7,
так как 6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Выполняем вычисления по действиям.
1 2
6 · 5 − 12 = 18
1) 6 · 5 = 30
2) 30 – 12 = (10 + 20) – 12 = 10 + (20 – 12) = 10 + 8 = 18
2 1
52 – 3 · 9 = 25
1) 3 · 9 = 27
2) 52 – 27 = 52 – (22 + 5) = (52 – 22) – 5 = 30 – 5 = 25
1 2
8 · 4 – 15 = 17
1) 8 · 4 = 4 · 8 = 32
2) 32 – 15 = 32 – (12 + 3) = (32 – 12) – 3 = 20 – 3 = 17
2 1
45 : (18 – 13) = 9
1) 18 – 13 = 5
2) 45 : 5 = 9
1 2
(27 + 27) : 9 = 6
1) 27 + 27 = 27 + (3 + 24) = (27 + 3) + 24 = 30 + 24 = 54
2) 54 : 9 = 6
2 1
24 : (11 – 7) = 6
1) 11 – 7 = 11 – (1 + 6) = (10 – 1) – 6 = 10 – 6 = 4
2) 24 : 4 = 6
Оформляем задание в тетрадь.
7 ∙ 8 = 56
6 ∙ 7 = 42
7 ∙ 5 = 35
49 : 7 = 7
63 : 9 = 7
42 : 6 = 7
6 ∙ 5 − 12 = 30 – 12 = 18
52 − 3 ∙ 9 = 52 – 27 = 25
8 ∙ 4 − 15 = 32 – 15 = 17
45 : (18 − 13) = 45 : 5 = 9
(27 + 27) : 9 = 54 : 9 = 6
24 : (11 − 7) = 24 : 4 = 6
Номер 3.
1) Запиши только те числа от 7 до 63, которые делятся на 7 без остатка.
2) Запиши все числа от 24 до 42. Подчеркни те, которые делятся на 6 без остатка.
1) 7, 14, 21, 28, 35, 42, 49, 56, 63.
2) 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
1) Делятся на 7 без остатка, то есть являются результатами таблицы умножения семи.
2) Делятся на 6 без остатка, то есть являются результатами таблицы умножения шести.
Вспомним таблицу умножения на 7.
-(2023).jpg)
Выпишем числа.
Результат умножения на 7 и есть те числа, которые без остатка делятся на 7:
7, 14, 21, 28, 35, 42, 49, 56, 63.
Выпишем все числа от 24 до 42.
24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
Рассуждаем.
Вспомним таблиц умножения на 6.
-(2023).jpg)
Результат умножения на 6 и есть те числа, которые без остатка делятся на 6.
Подчеркнем числа, которые делятся без остатка на 6:
24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
Оформим задание в тетрадь.
1) 7, 14, 21, 28, 35, 42, 49, 56, 63 – числа которые делятся без остатка на 7.
2) 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42.
Номер 4.
От доски длинной 8 м отпилили часть длиной 2 м. Во сколько раз больше оставшаяся часть доски, чем отпиленная?
Ответ:
1) 8 - 2 = 6 (м) осталось после отпила.
2) 6 : 2 = 3 (раза)
Ответ: в 3 раза оставшаяся часть доски больше, чем отпиленная.
Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Общая длина доски складывается из отрезанной части и оставшейся. Значит, чтобы узнать, сколько метров доски осталось, нужно из длины доски вычесть длину отрезанной части.
8 − 2 = 6 (м) осталось после отпила.
Продолжаем рассуждение.
Длина оставшейся части – 6 метров, а отрезанной – 2 метра. Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Значит, нужно длину оставшейся части разделить на длину отрезанной.
6 : 2 = 3 (раз) – во сколько раз больше оставшаяся часть доски, чем отпиленная.
Записываем ответ.
Ответ: в 3 раза больше оставшаяся часть доски больше, чем отпиленная.
Решение выражением:
(8 – 2) : 2 = 3 (раза)
Номер 5.
Реши уравнения, подбирая значения х.
х ∙ 7 = 42 36 : х = 4 9 ∙ х = 45 х : 6 = 6
Ответ:х ∙ 7 = 42
х = 42 : 7
х = 6
6 ∙ 7 = 42
42 = 42
Ответ: х = 6
36 : х = 4
х = 36 : 4
х = 9
36 : 9 = 4
4 = 4
Ответ: х = 9
9 ∙ х = 45
х = 45 : 9
х = 5
9 ∙ 5 = 45
45 = 45
Ответ: х = 5
х : 6 = 6
х = 6 ∙ 6
х = 36
36 : 6 = 6
6 = 6
Ответ: х = 36
1) Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
2) Вспомни зависимость между компонентами и результатом действия деления и умножения.
Рассмотрим уравнения.
х · 7 = 42,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
36 : х = 4,
х – неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного.
9 · х = 45,
х – неизвестный множитель.
Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель.
х : 6 = 6,
х – неизвестное делимое.
Чтобы найти неизвестное делимое, нужно значение частного умножить на делитель.
Найдём значение уравнения.
х ∙ 7 = 42
Вспомни таблицу умножения на 7. На сколько нужно умножить число 7, чтобы получилось 42. Это число 6, так как 6 · 7 = 42.
х = 6
36 : х = 4
Вспомни таблицу умножения на 4. На сколько нужно разделить число 36, чтобы стало 4. Это число 9, так как 4 · 9 = 36.
х = 9
9 ∙ х = 45
Вспомни таблицу умножения на 9. На сколько нужно умножить число 9, чтобы получилось 45. Это число 5, так как 5 · 9 = 45.
х = 5
х : 6 = 6
Вспомни таблицу умножения на 6. Какое число нужно разделить на 6, чтобы получилось 6. Это число 36, так как 6 · 6 = 36.
х = 36
Сделаем проверку.
х ∙ 7 = 42
Проверка: вместо х подставим число 6.
6 · 7 = 42
42 = 42 – верно.
36 : х = 4
Проверка: вместо х подставим число 9.
36 : 9 = 4, так как 4 · 9 = 36
4 = 4 – верно.
9 ∙ х = 45
Проверка: вместо х подставим число 5.
9 · 5 = 5 · 9 = 45
45 = 45 – верно.
х : 6 = 6
Проверка6 вместо х подставим число 36.
36 : 6 = 6, так как 6 · 6 = 36
6 = 6 – верно.
Оформим задание в тетрадь.
х ∙ 7 = 42
х = 6
Так как 6 · 7 = 42
36 : х = 4
х = 9
Так как 4 · 9 = 36
9 ∙ х = 45
х = 5
Так как 5 · 9 = 45
х : 6 = 6
х = 36
Так как 6 · 6 = 36
Задание внизу страницы.
Узнай площадь какой фигуры больше.

Нужно сосчитать количество клеточек, из которых состоит каждая фигура.
Зелёная фигура 42 клетки. Красная фигура 48 клеток.42 < 48
Ответ: вторая фигура больше.
1) Площадь фигуры – часть плоскости, на которой она лежит.
2) Чтобы узнать площадь фигуры, нужно посмотреть, из скольких одинаковых клеток она составлена.
Рассуждаем.
Чтобы определить площадь фигуры можно посчитать количество клеток.
В зелёной фигуре 42 клетки, значит и площадь равна 42.
Красная фигура – 48 клеток, значит площадь равна 48.
Продолжаем рассуждение.
Также площадь фигуры можно вычислить если разбить её на участки.
.jpg)
Зеленая фигура:
1 – 1 клетка.
2 – 3 строчки по 7 клеток – 3 ∙ 7 = 21 клетка.
3 – 11 клеток.
4 – 3 строчки по 2 клетки – 3 ∙ 2 = 6 клеток.
5 – 3 клетки.
Всего: 1 + 21 + 11 + 6 + 3 = 22 + 20 = 42 клетки – в зеленой фигуре.
Красная фигура:
1 – 1 клетка.
2 – 3 строчки по 4 клетки – 3 ∙ 4 = 12 клеток.
3 – 4 строчки по 7 клеток – 4 ∙ 7 = 28 клеток.
4 – 3 клетки.
5 – 3 клетки.
6 – 1 клетка.
Всего: 1 + 12 + 28 + 3 + 3 + 1 = 13 + 31 + 4 = 44 + 4 = 48 клеток.
Сравниваем фигуры.
42 клетки < 48 клеток, значит площадь зеленой фигуры меньше, чем красной фигуры.
Ответ: площадь красной фигуры больше.
Задание на полях страницы.
Какой предмет лишний?

Лишняя линейка. Она плоская.
Лишний мяч. У него нет углов.
Чтобы узнать, какой предмет лишний, рассмотри все. Какие признаки они имеют: цвет, размер, форма, отношение к пространству.
Рассмотрим предметы.
Предмет 1 – красный куб – объемная фигура.
Предмет 2 – оранжевый мяч – объемная фигура.
Предмет 3 – плоский угольник – плоский предмет.
Предмет 4 – коробка – объемная фигура.
Сделаем вывод
Угольник лишний предмет, так как это плоская фигу, а остальные объемные.
.С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.