Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 42
- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
.jpg "Изображение математика 3 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 42")
Номер 1.
В столовой израсходовали 8 кг муки и 24 кг крупы. Во сколько раз меньше израсходовали муки, чем крупы? Во сколько раз больше израсходовали крупы, чем муки?
Ответ:
24 : 8 = 3 (раза)
Ответ: в 3 раза меньше израсходовали муки, чем крупы; в 3 раза больше израсходовали крупы, чем муки.
1) Чтобы узнать, во сколько раз одно число больше другого, нужно большее число разделить на меньшее. Вычисляется делением.
2) Чтобы узнать, во сколько раз одно число меньше другого, нужно большее число разделить на меньшее. Вычисляется делением.
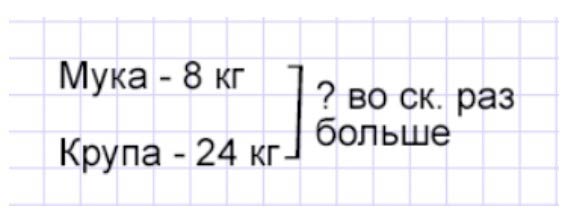
Оформляем условие в виде краткой записи.
Рассуждаем.
Зная, сколько израсходовали в столовой муки и крупы, можно узнать, во сколько раз израсходовали больше одного, чем другого, если количество большего продукта разделить на количество меньшего. Значит, нужно количество крупы разделить на количество муки.
24 : 8 = 3 (раза).
Записываем ответ.
Ответ: в 3 раза.
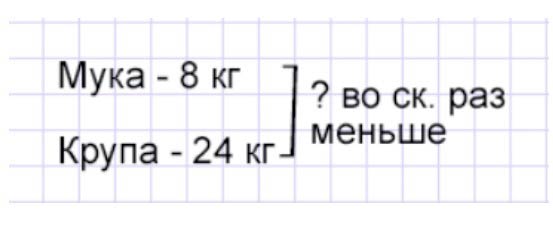
Оформляем условие в виде краткой записи.
Рассуждаем.
Зная, сколько израсходовали в столовой муки и крупы, можно узнать, во сколько раз израсходовали меньше одного, чем другого, если количество большего продукта разделить на количество меньшего. Значит, нужно количество крупы разделить на количество муки.
24 : 8 = 3 (раза).
Записываем ответ.
Ответ: в 3 раза.
Номер 2.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок - умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Помни о свойствах, на которые опираются арифметические действия:
Переместительное свойство – от перестановки мест слагаемых значение суммы не изменяется: а + в = в + а.
Сочетательное свойство – любые два соседних числа можно заменить их суммой: а + (в + с) = (а + в) + с.
Рассуждаем.
9 · (36 – 33)
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполним действие в скобках – вычитание, а потом умножение.
(40 – 8) : 4
В данном выражении присутствуют действия вычитание и деление, а также скобки. Вначале выполним действие в скобках – вычитание, а потом деление.
20 : 5 · 9
В данном выражении присутствуют действия умножение и деление – они равносильны. Поэтому выполняем действия по порядку слева направо.
5 · 6 : 3
В данном выражении присутствуют действия умножение и деление – они равносильны. Поэтому выполняем действия по порядку слева направо.
54 + 7 + 6 + 3 = (54 + 6) + (7 + 3)
Применим сочетательное и переместительное свойства сложения и сгруппируем слагаемые.
32 + 9 + 8 + 11 = (32 + 8) + (11 + 9)
Применим сочетательное и переместительное свойства сложения и сгруппируем слагаемые.
Расставляем порядок действий и выполняем вычисления.
2 1
9 · (36 – 33) = 27
1) 36 – 33 = 3
2) 9 ∙ 3 = 27
1 2
(40 – 8) : 4 = 8
1) 40 – 8 = 32
2) 32 : 4 = 8
1 2
20 : 5 ∙ 9 = 36
1) 25 : 5 = 4
2) 4 ∙ 9 = 36
1 2
5 ∙ 6 : 3 = 10
1) 5 ∙ 6 = 30
2) 30 : 3 = 10
1 3 2
54 + 7 + 6 + 3 = (54 + 6) + (7 + 3) = 70
1) 54 + 6 = 60
2) 7 + 3 = 10
3) 60 + 10 = 70
1 3 2
32 + 9 + 8 + 11 = (32 + 8) + (9 + 11) = 60
1) 32 + 8 = 40
2) 9 + 11 = 20
3) 40 + 20 = 60
Оформляем задание в тетрадь.
9 ∙ (36 − 33) = 9 · 3 = 27
(40 − 8) : 4 = 32 : 4 = 8
20 : 5 ∙ 9 = 4 · 9 = 36
5 ∙ 6 : 3 = 30 : 3 = 10
54 + 7 + 6 + 3 = (54 + 6) + (7 + 3) = 60 + 10 = 70
32 + 9 + 8 + 11 = (32 + 8) + (9 + 11) = 40 + 20 = 60
Номер 3.
Из 45 кг картофеля 30 кг отправили в столовую, а остальное расфасовали поровну в 5 пакетов. Сколько килограммов картофеля было в каждом пакете?
Ответ:
Было – 45 кг
Отправили – 30 кг
Расфасовали – 5 п. по ? кг
1-й способ решения:
1) 45 − 30 = 15 (кг) – картофеля расфасовали.
2) 15 : 5 = 3 (кг)
Ответ: 3 кг картофеля было в каждом пакете.
2-й способ решения: (45 – 30) : 5 = 15 : 5 =3 (кг) - было в каждом пакете. Ответ: 3 кг картофеля.
Помни о том, каков конкретный смысл умножения: умножение – замена одинаковых слагаемых произведением,
где а · 3,
а – первый множитель,
3 – количество множителей.
Оформляем условие в виде краткой записи.
Было – 45 кг
Отправили – 30 кг
Расфасовали – 5 п. по ? кг
Рассуждаем.
Общее количество картофеля складывается из количества отправленного картофеля и оставшегося. Значит, чтобы узнать сколько картофеля осталось, нужно из общего количества картофеля вычесть количество отправленного.
45 – 30 = 15 (кг) – картофеля расфасовали.
Продолжаем рассуждение.
Теперь нам известно, сколько картофеля осталось для расфасовки. Весь этот картофель расфасовали в 5 одинаковых пакетов. Одинаковых, т.е. количество картофеля в каждом равное. Соответственно, чтобы узнать, сколько картофеля было в одном пакете, нужно общее количество картофеля разделить на количество пакетов.
15 : 5 = 3 (кг) – в каждом пакете.
Записываем ответ.
Ответ: 3 кг.
Решение выражением:
45 – 30) : 5 = 3 кг.
Номер 4.
Ответ:
76 + 24 = 100
89 + 0 = 89
56 - 36 = 20
72 - 48 = 24
32 - 0 = 32
1) Вспомни названия компонентов при вычитании, и зависимость между компонентами и результатом действия вычитания;
2) вспомни названия компонентов действия сложения и зависимости между компонентами и результатом действия сложения;
3) Вычисление значений выражения сводится к применению правил:
Правило вычитания суммы из числа: а – (в + с) = (а – в) – с.
Правило вычитания числа из суммы: (а + в) – с = (а – с) + в.
Вычисляем недостающие числа.
30 – 18 = 30 – (10 + 8) = (30 – 10) – 8 = 20 – 8 = 12
Число 18 разложим на сумму чисел 10 и 8. Вначале из числа 30 вычтем число 10, а потом число 8.
Использовали правило вычитания суммы из числа.
100 – 24 = 100 – (20 + 4) = (100 – 20) – 4 = 80 – 4 = 76
Число 24 разложим на сумму чисел 20 и 4. Вначале из числа 100 вычтем число 20, а потом число 4.
Использовали правило вычитания суммы из числа.
89 – 89 = 0
Если из числа вычесть само число, то получится нуль.
56 – 20 = (50 + 6) – 20 = (50 – 20) + 6 = 30 + 6 = 36
Число 50 разложим на сумму чисел 50 и 6. Вначале из числа 50 вычтем число 20, а потом прибавим число 6.
Использовали правило вычитания числа из суммы.
24 + 48 = 24 + (46 + 2) = (24 + 46) + 2 = 70 + 2 = 72
Число 48 разложим на сумму чисел 46 и 2. Вначале к числу 24 прибавим число 46, а потом число 2.
32 – 32 = 0
Если из числа вычесть само число, то получится нуль.
Запишем числа в таблицу.
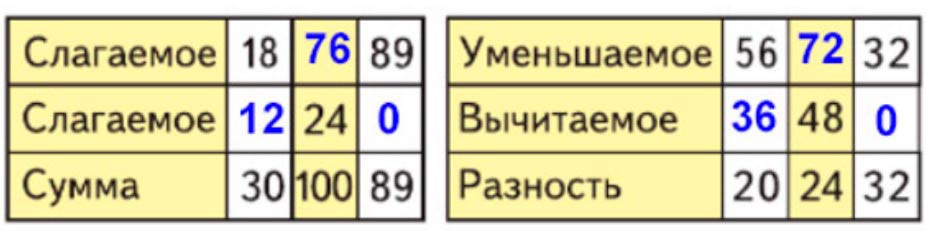
Задание внизу страницы
Начерти два отрезка: первый длиной 12 см, а второй на 8 см короче. Во сколько раз длина второго отрезка меньше длины первого?
Ответ:
12 − 8 = 4 (см)
12 : 4 = 3 (р.)
Ответ: в 3 раза второй отрезок короче первого.
1) Отрезок – геометрическая фигура, часть прямой, ограниченная с двух сторон точками. Отрезок имеет длину, т.е расстояние от точки до точки.
2) «на 8 см короче», значит, вычисляется вычитанием.
3) Чтобы узнать, во сколько раз меньше, нужно больше число разделить на меньшее.
Оформляем условие в виде краткой записи.
.jpg)
Рассуждаем.
Длина первого отрезка – 12 см, а второго – на 8 см короче. Короче, значит, меньше. Поэтому длина второго отрезка такая же, как первого, но без 8 см. Соответственно, чтобы узнать, какова длина второго отрезка, нужно из длины первого вычесть 8 см. вычисляется вычитанием.
12 – 8 = 4 (см) – длина второго отрезка.
Продолжаем рассуждение.
Зная длины обоих отрезков, ответим на вопрос задачи. Чтобы узнать, во сколько раз длина второго отрезка меньше длины первого, нужно длину второго отрезка разделить на длину первого.
12 : 4 = 3 (раза).
Начертим отрезки.
Нужно начертить два отрезка с помощью линейки: длина первого – 12 см; длина второго – 4 см.
.jpg)
Записываем ответ.
Ответ: в 3 раза.
Решение выражением:
12 : (12 – 8) = 3 (раза)
Задание на полях страницы
Цепочка:
Ответ:
6 ∙ 3 = 18 18 : 2 = 9 9 : 3 = 3 3 ∙ 8 = 24
1) Выполни действия по порядку. Первая лиловая шестеренка – число, с которого начинать действие. Последняя шестеренка – число результат.
2) Переместительное свойство – от перестановки мест множителей значение произведения не изменяется : а · в = в · а.
Выполним устные рассуждения.
6 · 3 = 3 · 6 = 18
Применяем переместительное свойство умножения и таблицу умножения на 3.
18 : 2 = 9
Вспомним таблицу умножения на 2. При умножении какого числа на 2 в результате получим 18. Это число 9, так как 2 · 9 = 18.
9 : 3 = 3
Вспомним таблицу умножения на 3. При умножении какого числа на 3 в результате получим 9. Это число 3, так как 3 · 3 = 9.
3 · 8 = 24
Применяем таблицу умножения на 3.
Оформляем задание в тетрадь.
6 · 3 = 18
18 : 2 = 9
9 : 3 = 3
3 · 8 = 24
6 · 3 = 18 → 18 : 2 = 9 → 9 : 3 = 3 →3 · 8 = 24
Странички для любознательных
Номер 1.
Заяц, волк и лиса соревновались в беге. Медведь, белка и сова наблюдали за ними. на вопрос, кто прибежал первым, кто – вторым, медведь и белка ответили так:
Заяц был первым, лиса – второй.
Заяц был вторым, первым был волк.
А сова заметила, что одно из утверждений каждого из них было верным, а другое ошибочным.
Кто же был первым и кто был вторым?
Закончи рассуждения.
Заяц не мог быть первым, так как если заяц первый, то медведь ошибся два раза, а по условию задачи ... Значит, лиса была ..., а волк – ... .
Заяц не мог быть первым, так как если заяц первый, то медведь ошибся два раза, а по условию задачи медведь ошибся только в одном условии. Значит, лиса была вторая, а волк – первым.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.