Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 36

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 1.
Сделай рисунок к задаче и реши ее.
Купили 5 зеленых мячей, а красных в 3 раза больше. Сколько красных мячей купили?

5 ∙ 3 = 15 (м.)
Ответ: 15 красных мячей купили.
«в 3 раза больше» - это значит 3 раза по столько, т.е. число нужно умножить на 3, увеличить в 3 раза.
Оформляем условие в виде рисунка.
По условию задачи сказано, что зелёных мячей – 5. Значит в первой строчке нарисуем 5 зелёных мячей.
Так же знаем, что красных мячей в 3 раза больше, чем зелёных. Значит, нужно нарисовать три строчки по 5 красных мячей.
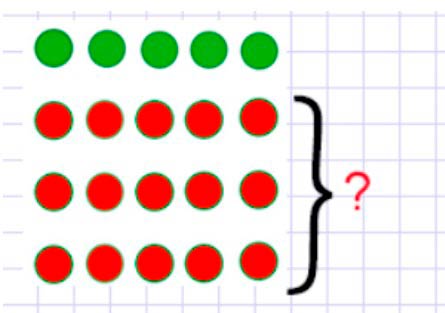
Рассуждаем.
Узнаем количество красных мячей.
По рисунку видно, что красных мячей 3 раза по 5, значит число 5 сложим три раза.
5 + 5 + 5 = 15 (м.)
5 · 3 = 3 · 5 = 15 (м.) – красных.
Записываем ответ.
Ответ: 15 мячей.
Номер 2.
1) В магазине продали 9 тетрадей по цене 3 р. за каждую. Сколько денег выручили за эти тетради?
2) Составь и реши две задачи, обратные данной.
1)

9 ∙ 3 = 27 (рублей) – выручили за тетради.
Ответ: 27 рублей выручили за эти тетради.
2) Обратная задача 1:
В магазине продали 9 тетрадей за 27 рублей. Сколько стоит одна тетрадь?

27 : 9 = 3 (руб.)
Ответ:3 рубля стоимость одной тетради.
Обратная задача 2:
В магазине продали тетради на 27 рублей. Сколько тетрадей продали в магазине, если одна тетрадь стоит 3 рубля.

27 : 3 = 9 (т.) Ответ: 9 тетрадей продали в магазине.
Данная задача: вида «цена тетради, количество тетрадей, общая стоимость» характеризуется зависимостями между компонентами:
Цена тетради · количество тетрадей = общая стоимость.
Общая стоимость : цена тетради = количество тетрадей.
Общая стоимость : количество тетрадей = цена тетради.
Оформляем условие в виде таблицы.

Рассуждаем.
В магазине продали 9 тетрадей по цене за 3 рубля за каждую. Общая стоимость тетрадей складывается из стоимостей всех трех тетрадей. Поэтому, чтобы узнать, сколько стоят три тетради, нужно их цены сложить. Но цена тетради одинакова, поэтому сложение одинаковых слагаемых можно заменить умножением.
3 · 9 = 27 (руб.) – стоимость 9 тетрадей.
Записываем ответ.
Ответ: 27 рублей.
Составим обратную задачу.
В самой задаче было неизвестно общая стоимость тетрадей.
В обратной задаче найдём стоимость одной тетради, если известно, что продали 9 тетрадей за сумму 27 рублей.
Оформляем условие в виде таблицы.

Рассуждаем.
В магазине продали 9 тетрадей за 27 рублей. Но их количество неизвестно. При этом тетради одинаковые, т.е. каждая стоит равное количество денег.
Из таблицы видно, что чтобы узнать, какова цена тетради, нужно общую стоимость тетрадей разделить на количество тетрадей.
27 : 9 = 3 (руб.) – стоимость одной тетради.
Записываем ответ.
Ответ: 3 рубля.
Составим обратную задачу.
В самой задаче было неизвестно общая стоимость тетрадей.
В обратной задаче найдём количество тетрадей, если известно, что стоимость одной тетради – 3 рубля, а общая стоимость – 27 рублей.
Оформляем условие в виде таблицы.

Рассуждаем.
В магазине продали тетради на 27 рублей по 3 рубля за тетрадь. Их количество неизвестно, но цена одинаковая, т.е. количество денег, затраченное на каждую тетрадь одинаково.
Из таблицы видно, что чтобы узнать, сколько тетрадей было куплено, нужно общую стоимость разделить на цену тетради.
27 : 3 = 9 (шт.) – количество купленных тетрадей.
Записываем ответ.
Ответ: 9 тетрадей.
Номер 3.
Найди уравнения, которые ты пока не можешь решить. Исправь их и реши.
Ответ:
Исправляем в уравнениях действия и находим значение х.

Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассмотрим уравнения.
78 + х = 40
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
Решить такое уравнение мы пока не можем, ведь значение суммы меньше слагаемого.
х – 23 = 60
х – неизвестное уменьшаемое. Чтобы найти неизвестное уменьшаемое, нужно к значению разности прибавить вычитаемое.
Решить такое уравнение можем.
50 – х = 64
х – неизвестное вычитаемое. Чтобы найти неизвестное вычитаемое нужно из уменьшаемого вычесть разность.
Решить такое уравнение пока что не можем, ведь уменьшаемое меньше разности.
Исправим уравнения.
78 + х = 40
Заменим арифметическое действие сложение на вычитание.
Прилучим новое уравнение:
78 – х = 40
50 – х = 64
Исправим арифметическое действие вычитание на сложение.
Получим новое уравнение:
78 – х = 0
Решим получившиеся уравнения.
78 – х = 40
х – неизвестно вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
х = 78 – 40
х = 38
50 + х = 64
х – неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
х = 64 – 50
х = 14
Номер 4.
1) Найди значение выражения 1 ∙ b при b = 4, b = 79, b = 98, b = 100.
2) Найди значение выражения 0 ∙ k при k = 3, k = 81, k = 90, k = 100.
1) 1 ∙ 4 = 4
1 ∙ 79 = 79
1 ∙ 98 = 98
1 ∙ 100 = 100
2) 0 ∙ 3 = 0
0 ∙ 81 = 0
0 ∙ 90 = 0
0 ∙ 100 = 0
1) 1 · b, значит, умножить 1 на число.
2) 0 · k, значит, умножить 0 на число.
Рассуждаем.
Выражение 1 · b основано на правиле – если единицу умножить на любое число, то получится это число: 1 · b = b.
Выражение 0 · k основано на правиле – если 0 умножить на любое число, то получится ноль: 0 · k = 0.
Вычислим.
1 · b, если:
b = 1, то 1 ∙ 4 = 4
b = 79, то 1 ∙ 79 = 79
b = 98, то 1 ∙ 98 = 98
b = 100, то 1 ∙ 100 = 100
0 ∙ k, при:
k = 3, то 0 ∙ 3 = 0
k = 81, то 0 ∙ 81 = 0
k = 90, то 0 ∙ 90 = 0
k = 100, то 0 ∙ 100 = 0
Номер 5.
Ответ:
9 ∙ 4 = 36 32 : 4 = 8
8 ∙ 4 = 32 14 : 7 = 2
7 ∙ 4 = 28 24 : 6 = 4
20 : 4 = 5
36 : 9 = 4
28 : 4 = 7

1) Вычисление значений выражения сводится к применению правил и свойств:
а – (в + с) = (а – в) – с – вычитание суммы из числа:
(а + в) – с = (а – с) + в – вычитание числа из суммы;
а · b = b · a – переместительное свойство умножения.
2) Вспомни таблицу умножения на 4.
Рассмотрим выражения.
9 · 4 = 4 · 9 = 36
4 – одинаковое слагаемое, 9 – количество одинаковых слагаемых.
Применим переместительное свойство умножения.
8 · 4 = 4 · 8 = 32,
4 – одинаковое слагаемое, 8 – количество одинаковых слагаемых.
Применим переместительное свойство умножения.
7 · 4 = 4 · 7 = 28,
4 – одинаковое слагаемое, 7 – количество одинаковых слагаемых.
Применим переместительное свойство умножения.
32 : 4 = 8
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 32? Это число 8, так как 4 · 8 = 32.
14 : 7 = 2
Вспомним таблицу умножения. Какое число при унижении на 7 даёт результат 14? Это число 2, так как 2 · 7 = 14.
24 : 6 = 4
Вспомним таблицу умножения. Какое число при умножении на 6 даёт результат 24? Это число 4, так как 4 · 6 = 24.
20 : 4 = 5
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 20? Это число 5, так как 4 · 5 = 20.
36 : 9 = 4
Вспомним таблицу умножения. Какое число при умножении на 9 даёт результат 36? Это число 4, так как 4 · 9 = 36.
28 : 4 = 7
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 28? Это число 7, так как 4 · 7 = 28.
42 + (20 – 8) = 42 + 12 = (40 + 10) + (2 + 2) = 50 + 4 = 54
Первый действием выполним вычисления в скобках – действие вычитание. Потом по разрядно сложим числа 42 и 12.
50 – (17 – 9) = 50 – 8 = (40 + 10) – 8 = 40 + (10 – 8) = 40 + 2 = 42
Вначале выполним вычисления в скобках – вычитание. После число 50 разложим на сумму чисел 40 и 10. Из 10 вычтем число 8 и затем к числу 40 прибавим полученную разность.
Используем правило вычитание числа из суммы.
70 – (38 + 7) = 70 – 45 = 70 – (40 + 5) = (70 – 40) – 5 = 30 – 5 = 35
Вначале выполним вычисления в скобках – сложение. После число 45 разложим на сумму чисел 40 и 5. Из числа 70 вычтем число 40 и затем из полученной разности вычтем число 5.
Используем правило вычитание суммы из числа.
Оформляем задание в тетрадь.
9 ∙ 4 = 36
8 ∙ 4 = 32
7 ∙ 4 = 28
32 : 4 = 8
14 : 7 = 2
24 : 6 = 4
20 : 4 = 5
36 : 9 = 4
28 : 4 = 7
42 + (20 − 8) = 42 + 12 = 54
50 − (17 − 9) = 50 – 8 = 42
70 − (38 + 7) = 70 – 45 = 25
Номер 6.
1) Сколько квадратов на чертеже?
2) Как получить 3 одинаковых квадрата, переложив 2 палочки? Найди несколько решений.
3) Как получить 4 одинаковых квадрата, если добавить 2 палочки?

1) Квадрат – геометрическая фигура, четырехугольник, у которого все стороны равны.
2) Стороны квадрата – палочки, которые можно перекладывать, убирать и добавлять.
Рассмотрим чертёж.
На чертеже 2 квадрата: один большой и один маленький внутри большого.
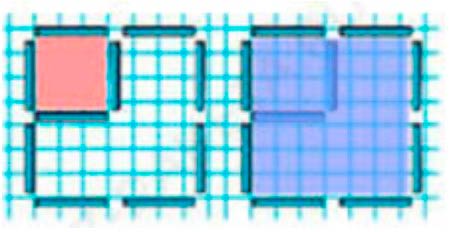
Ответ: 2 квадрата.
Получим 3 квадрата.
1) Чтобы получить три квадрата, нам нужно переложить любые две боковые рядом стоящие боковые палочки.
Покажем варианты какие палочки можно переложить – обозначены красным цветом.
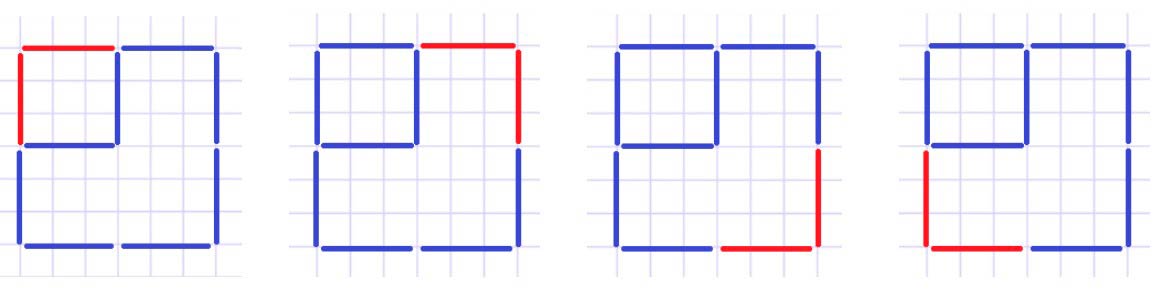
2) Теперь эти палочки нужно переместить внутрь фигуры.
Покажем полученные варианты.
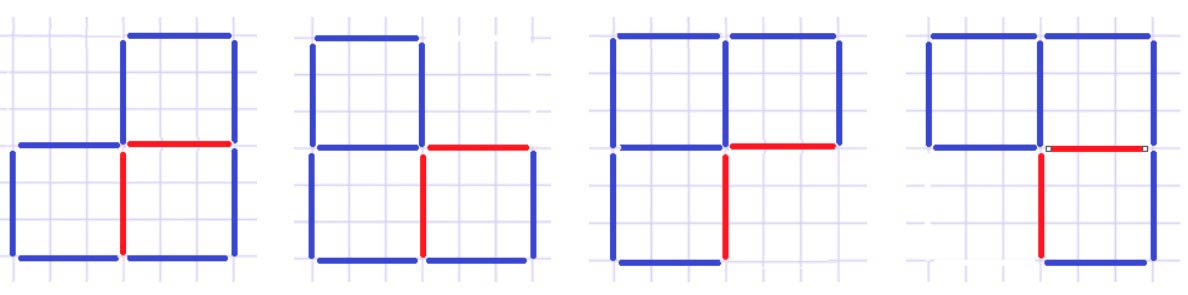
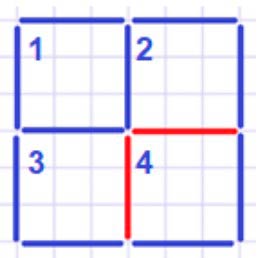
Получим 4 квадрата.
Чтобы на чертеже получилось 4 одинаковых квадрата, нужно две палочки добавить внутри фигуры – показано красным цветом.
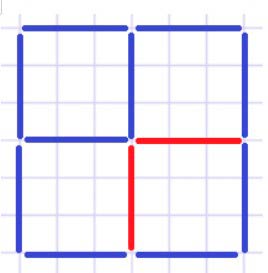
Тогда мы получим 4 одинаковых маленьких квадрата.
Задание внизу страницы
Начерти два отрезка: длина первого 8 мм, а длина второго в 4 раза больше.
Ответ:
1) Отрезок – геометрическая фигура, часть прямой, ограниченная с двух сторон точками.
2) Отрезок имеет длину, т.е расстояние от точки до точки.
3) Длина выражается в числовых значениях единиц измерения. При этом помни о соотношении единиц измерения длины:
1 см = 10 мм.
1 дм = 10 см.
Узнаем длину второго отрезка.
.jpg)
Длина первого отрезка – 8 мм, а второго – в 4 раза больше.
В 4 раза больше, значит, что длина второго отрезка 4 раза по 8 мм, вычислим умножением.
8 · 4 = 32 (мм) – длина второго отрезка.
32 мм = 30 мм + 2 мм = 3 см 2 мм.
Начертим отрезки.
С помощью линейки начертим отрезки: первый длиною 8 мм и второй – 3 см 2 мм.
.jpg)
Задание на полях страницы
Цепочка:

Ответ:
28 : 4 = 7 7 + 5 = 12 12 : 4 = 3
1) Выполни действия по порядку.
2) Первая красная шестеренка – число, с которого начинать действие.
3) Последняя шестеренка – число результат.
4) Вычисление значений выражения сводится к применению правила:
а + (в + с) = (а + в) + с – прибавление суммы к числу.
Выполним устные рассуждения.
28 : 4 = 7
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 28? Это число 7, так как 4 · 7 = 28.
7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 10 + 2 = 12
Число 7 разложим на сумму чисел 3 и 2. Вначале число 7 сложим с числом 3, а потом к полученной сумме прибавим число 2.
Использовали правило прибавление суммы к числу.
12 : 4 = 3
Вспомним таблицу умножения на 4. Какое число при умножении на 4 даёт результат 12? Это число 3, так как 4 · 3 = 12.
Оформляем задание в тетрадь.
28 : 4 = 7
7 + 5 = 12
12 : 4 = 3
28 : 4 = 7 → 7 + 5 = 12 → 12 : 4 = 3
Номер 1.
За 5 дней в семье израсходовали 10 кг овощей. Сколько овощей израсходовали за 3 дня, если каждый день расходовали овощей поровну?

1) 10 : 5 = 2 (кг) – овощей, за один день.
2) 2 ∙ 3 = 6 (кг) – овощей, за три дня.
Ответ: 6 кг овощей расходовали в каждый день поровну.
Данная задача: вида «расход в 1 день, количество дней, общий расход» характеризуется зависимостями между компонентами:
Расход в 1 день · количество дней = общий расход.
Общий расход : расход в 1 день = количество дней.
Общий расход : количество дней = расход в 1 день.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
За 5 дней в семье израсходовали 10 кг овощей, но неизвестно, сколько кг овощей расходовали в каждый из дней. При этом, расход в каждый день одинаковый. Поэтому, чтобы узнать, сколько овощей расходовали за 1 день, нужно общий расход овощей разделить на количество дней.
10 : 5 = 2 (кг) – овощей, за один день.
Продолжаем рассуждение.
В первом действии мы узнали расход овощей в 1 день. Теперь, зная расход и количество дней, нужно узнать общий расход овощей. Значит, чтобы узнать каков общий расход овощей, нужно сложить расход овощей в каждый из 3 дней.
Но расход овощей в каждый из дней одинаковый, поэтому сложение одинаковых слагаемых можно заменить умножением.
2 · 3 = 6 (кг) – овощей за три дня.
Записываем ответ.
Ответ: 6 кг овощей.
Решение выражением:
10 : 5 ∙ 3 = 6 (кг)
Номер 2.
За 6 м ленты заплатили 18 р. Сколько рублей стоит 9 м такой ленты?
Ответ:
1) 18 : 6 = 3 (руб.) – стоит 1 м ленты.
2) 3 ∙ 9 = 27 (руб.)
Ответ: 27 рублей стоит 9 м ленты.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
За 6 метров ленты заплатили 18 рублей. Соответственно, неизвестна цена одного метра ленты.
При этом цена метра ленты одинаковая, и что чтобы узнать цену метра ленты, нужно стоимость всех метров ленты разделить на количество купленной ленты.
18 : 6 = 3 (руб.) – стоимость 1 метра ленты.
Продолжаем рассуждение.
Теперь мы знаем цену одного метра ленты. Количество купленной ленты – 9 метров.
Неизвестна общая стоимость ленты. Чтобы узнать, сколько стоит лента, нужно сложить стоимости каждого купленного метра ленты.
Но цена ленты при этом одинаковая, значит, что за каждый метр ленты заплатили равное количество денег. Соответственно, сложение одинаковых слагаемых можно заменить умножением.
3 · 9 = 27 (руб.) – стоимость 9 метров ленты.
Записываем ответ.
Ответ: 27 рублей.
Решение выражением:
18 : 6 ∙ 9 = 27 (руб.)
Номер 3.
54 : 6 (52 - 31) : 3
42 : 6 54 : (16 - 7)
40 : 8 35 : (30 - 23)
9 : 3 6 · 5 : 10
16 : 4 3 · 8 : 6
36 : 6 5 · 4 : 10
54 : 6 = 9 9 : 3 = 3
42 : 6 = 7 16 : 4 = 4
40 : 8 = 5 36 : 6 = 6

1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
4) Для выполнения задания обращайся к таблице умножения и деления с числом 2, 3,4, 5, 6.
Выполним деление.
54 : 6 = 9,
Вспомним таблицу умножения на 6. При умножении какого числа на 6 получится 54? Это число 9, так как 6 · 9 = 54.
42 : 6 = 7,
Вспомним таблицу умножения на 6. При умножении какого числа на 6 получится 42? Это число 7, так как 6 · 7 = 42.
36 : 9 = 4,
Вспомним таблицу умножения. При умножении какого числа на 9 получится 36? Это число 4, так как 4 · 9 = 36.
40 : 8 = 5,
Вспомним таблицу умножения. При умножении какого числа на 8 получится 40? Это число 5, так как 5 · 8 = 40.
Выполним вычисления по действиям.
1 2
(52 − 31) : 3 = 7
1) 52 – 31 = (50 – 20) + (2 – 1) = 20 + 1 = 21
2) 21 : 3 = 7,так как 3 · 7 = 21
2 1
54 : (16 – 7) = 6
1) 16 – 7 = 16 – (6 + 1) = (16 – 6) – 1 = 10 – 1 = 9
2) 54 : 9 = 6, так как 6 · 9 = 54
1 2
(12 + 18) : 6 = 5
1) 12 + 18 = (10 + 10) + (2 + 8) = 20 + 10 = 30
2) 30 : 6 = 5, так как 6 · 5 = 30
2 1
35 : (30 – 23) = 5
1) 30 – 23 = (20 + 10) – (20 + 3) = (20 – 20) + (10 – 3) = 7
2) 35 : 7 = 5, так как 5 · 7 = 35
Выполним деление.
9 : 3 = 3
Вспомним таблицу умножения на 3. При умножении какого числа на 3 получится 9? Это число 3, так как 3 · 3 = 9.
16 : 4 = 4
Вспомним таблицу умножения на 4. При умножении какого числа на 4 получится 16? Это число 4, так как 4 · 4 = 16.
25 : 5 = 5
Вспомним таблицу умножения на 5. При умножении какого числа на 5 получится 25? Это число 5, так как 5 · 5 = 25.
36 : 6 = 6
Вспомним таблицу умножения на 6. При умножении какого числа на 6 получится 36? Это число 6, так как 6 · 6 = 36.
Выполним вычисления по действиям.
Расставим порядок действий и вычислим.
В данных выражениях присутствуют действия умножение и деление – они равносильны, поэтому выполняем действия по порядку слева направо.
1 2
6 · 5 : 10 = 3
1) 6 · 5 = 30
2) 30 : 10 = 3, так как 3 · 10 = 30
1 2
3 · 8 : 6 = 4
1) 3 · 8 = 24
2) 24 : 6 = 4, так как 6 · 4 = 24
1 2
5 · 7 : 5 = 7
1) 5 · 7 = 35
2) 35 : 5 = 7
1 2
5 · 4 : 10 = 2
1) 5 · 4 = 20
2) 20 : 10 = 2, так как 2 · 10 = 20
Оформим задание в тетрадь.
54 : 6 = 9
42 : 6 = 7
36 : 9 = 4
40 : 8 = 5
(52 − 31) : 3 = 21 : 3 = 7
54 : (16 − 7) = 54 : 9 = 6
(12 + 18) : 6 = 30 : 6 = 5
35 : (30 − 23) = 35 : 7 = 5
9 : 3 = 3
16 : 4 = 4
25 : 5 = 5
36 : 6 = 6
6 ∙ 5 : 10 = 30 : 10 = 3
3 ∙ 8 : 6 = 24 : 6 = 4
5 ∙ 7 : 5 = 35 : 5 = 7
5 ∙ 4 : 10 = 20 : 10 = 2
Номер 4.


1) b · 6, значит, увеличить число b в 6 раз, вычисляется умножением.
2) Вспомни, переместительное свойство умножения – а · b = b · a – от перестановки мест слагаемых, произведение не изменяется.
При вычислении значении буквенного выражения нужно вместо неизвестной буквы подставить заданное число.
b · 6
При b = 1, 1 · 6 = 6,
где 1 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 2, 2 · 6 = 12,
где 2 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 3, 3 · 6 = 18,
где 3 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 4, 4 · 6 = 24,
где 4 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 5, 5 · 6 = 30,
где 5 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 6, 6 · 6 = 36,
где 6 – одинаковое слагаемое, а 6 – количество одинаковых слагаемых.
При b = 7, 7 · 6 = 6 · 7 = 42,
где 6 – это одинаковое слагаемое, а 7– количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
При b = 8, 8 · 6 = 6 · 8 = 48,
где 6 – это одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
При b = 9, 9 · 6 = 6 · 9,
где 6 – это одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
Применяем переместительное свойство умножения.
Заполним таблицу.
.jpg)
Номер 5.
На диаграмме показано, сколько килограммов моркови заготовил фермер на корм кроликам на 3 месяца: сентябрь, октябрь, ноябрь.
Начерти такую диаграмму и дополни её, зная, что за декабрь заготовили 60 кг моркови.


Вспомним, что такое столбчатые диаграммы.
Рассуждаем.
Столбчатые диаграммы – это рисунки или чертежи, на которых числа и значения величин изображены столбиками. Для построения столбиков обязательно используют одну и ту же мерку. Столбики можно «поставить», а можно «положить».
Строим диаграмму.
.jpg)
Оформляем задание в тетрадь.
Задание внизу страницы
6 одинаковых игрушечных машинок стоят 48 р. Сколько рублей стоят 5 таких машинок?
Ответ:
1) 48 : 6 = 8 (р.) – цена 1 машинки.
2) 8 ∙ 5 = 40 (р.)
Ответ: 5 машинок стоят 40 рублей.
Данная задача: вида «цена, количество, стоимость» характеризуется зависимостями между компонентами:
Цена · количество = стоимость.
Стоимость : цена = количество.
Стоимость : количество = цена.
Оформляем условие в виде таблицы.
.jpg)
Рассуждаем.
6 одинаковых игрушечных машинок стоит 48 рублей. Соответственно, неизвестна цена одной машинки.
При этом цена машинок одинаковая, и что чтобы узнать цену машинки, нужно стоимость машинок разделить на количество.
48 : 6 = 8 (руб.) – цена одной машинки.
Продолжаем рассуждение.
Теперь нам известна цена машинки. Количество машинок – 5 штук.
Нам неизвестная общая стоимость всех машинок. Она складывается из цен всех 5 машинок. Значит, чтобы узнать, сколько стоят все машинки, нужно стоимости машинок сложить.
Но цена машинок одинаковая, т.е, каждая стоит равное количество денег. Поэтому сложением одинаковых слагаемых можно заменить умножением.
8 · 5 = 40 (руб.) – цена 5 машинок.
Записываем ответ.
Ответ: 40 рублей.
Решение выражением:
48 : 6 ∙ 5 = 40 (руб.)
Задание на полях страницы
Какое выражение лишнее?
48 : 6
12 : 6
24 : 6
6 : 6
54 : 6
42 : 7
7 · 6
Лишнее выражение 7 ∙ 6 так как это пример на умножение, а все прочие на деление.
Чтобы понять, какое выражение лишнее, нужно рассмотреть их и сравнить: из каких компонентов состоит, на каких арифметических действиях основаны, каковы их значения.
Вычислим выражения.
Опишем все выражения, вычислим их значения.
48 : 6 = 8,
так как 6 · 8 = 48,
где 6 – одинаковое слагаемое, а 8 – количество одинаковых слагаемых.
12 : 6 = 2,
так как 6 · 2 = 12,
где 6 – одинаковое слагаемое, а 2 – количество одинаковых слагаемых.
24 : 6 = 4,
так как 6 · 4 = 24,
где 6 – одинаковое слагаемое, а 4 – количество одинаковых слагаемых.
6 : 6 = 1, так как 6 · 1 = 6,
где 6 – одинаковое слагаемое, а 1 – количество одинаковых слагаемых.
54 : 6 = 9,
так как 6 · 9 = 54,
где 6 – одинаковое слагаемое, а 9 – количество одинаковых слагаемых.
42 : 7 = 6,
так как 6 · 7 = 42,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
7 · 6 = 6 · 7 = 42,
Применяем переместительное свойство умножения,
где 6 – одинаковое слагаемое, а 7 – количество одинаковых слагаемых.
Делаем вывод.
Получается, что лишним может быть выражение: 7 · 6, потому что это единственное выражение, основанное на арифметическом действии умножения.
Ответ: 7 · 6 – лишнее выражение.
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.