Математика 3 класс учебник Моро, Волкова 1 часть ответы – страница 31

- Тип: ГДЗ, Решебник.
- Авторы: Моро М.И., Бантова М.А., Бельтюкова Г.В. и др.
- Часть: 1.
- Год: 2020-2023.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.

Номер 16.
Внучка ехала на метро навестить бабушку. До пересадки она проехала 8 станций, после пересадки еще 7. Сколько всего станций проехала внучка?
Ответ:8 + 7 = 15 (ст.) – всего проехала внучка. Ответ: 15 станций проехала внучка всего.
«Всего» – вычисляется сложением.
Оформляем условие в виде краткой записи или чертежа.
Краткая запись:

Чертёж:
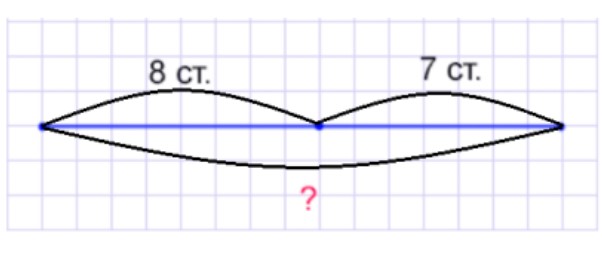
Рассуждаем.
Общее количество станций, которые проехала внучка, складывается из количества станций, которые она проехала до пересадки и после. Поэтому. Чтобы узнать, сколько станций проехала внучка всего, нужно сложить количество станций до и после пересадки.
8 + 7 = 15 (ст.) – проехала внучка.
Записываем ответ.
Ответ: 15 станций.
Номер 17.
За границу отправляются туристы: на самолете 20 человек, на поезде на 35 человек больше, чем на самолете, а на автобусе на 22 человека меньше, чем на поезде. Поставь вопрос и реши задачу.
Ответ:Сколько туристов поедет на автобусе?

1) 20 + 35 = 55 (т.) – поедет на поезде. 2) 55 − 22 = 33 (т.) – поедет на автобусе. Ответ: 33 туриста поедет на автобусе.
1) Вопрос: Сколько туристов поедет на автобусе?
1) «на 35 больше» – вычисляется сложением.
2) «на 22 меньше» – вычисляется вычитанием.
Оформляем условие в виде краткой записи.
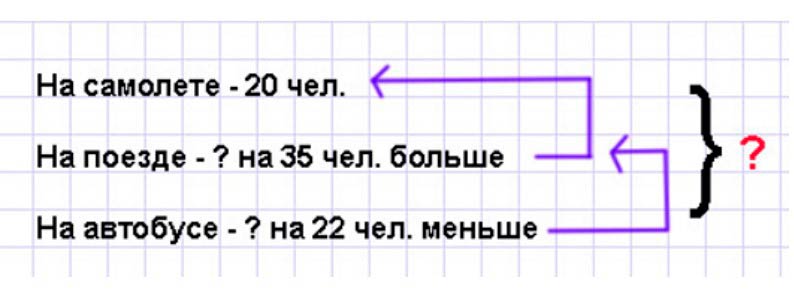
Рассуждаем.
На самолете поехали 20 человек, а на поезде – на 35 человек больше. Значит, что на поезде поехали столько человек, сколько на самолете и еще 35 человек.
Чтобы узнать, сколько человек поехали на поезде, нужно к количеству человек на самолете прибавить 35 человек.
20 + 35 = 55 (чел.) – на поезде.
Продолжаем рассуждения.
На автобусе поехало на 22 человека меньше, чем на поезде. Значит, что на автобусе поехали столько человек, сколько на автобусе, но без 22 человек. Чтобы узнать, сколько человек поехало на автобусе, нужно из количества человек, которые поехали на поезде вычесть 22 человека.
55 – 22 = 33 (чел.) – на автобусе.
Записываем ответ.
Ответ: 33 человека.
Решение выражением:
(20 + 35) – 22
Номер 18.
Ответ:
1) Помни о порядке выполнения арифметических действий и что скобки влияют на порядок выполнения действий.
2) Сначала выполняются действия в скобках, умножение или деление, а потом – сложение или вычитание. Слева направо.
3) Затем – действия вне скобок – умножение или деление, а потом – сложение или вычитанием. Слева направо.
Рассуждаем.
8 · (49 – 46)
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом умножение.
3 · (21 – 12)
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом умножение.
7 · (30 – 28)
В данном выражении присутствуют действия вычитание и умножение, а также скобки. Вначале выполняем действие в скобках – вычитание, а потом умножение.
40 : 4 · 3
В данном выражении присутствуют действия умножение и деление – они равноправны. Поэтому действия выполняем по порядку справа налево.
50 : 5 · 6
В данном выражении присутствуют действия умножение и деление – они равноправны. Поэтому действия выполняем по порядку справа налево.
70 : 7 · 9
В данном выражении присутствуют действия умножение и деление – они равноправны. Поэтому действия выполняем по порядку справа налево.
1 · 30 : 10
В данном выражении присутствуют действия умножение и деление – они равноправны. Поэтому действия выполняем по порядку справа налево.
1 · 60 : 6
В данном выражении присутствуют действия умножение и деление – они равноправны. Поэтому действия выполняем по порядку справа налево.
1 · 80 : 10
В данном выражении присутствуют действия умножение и деление – они равноправны. Поэтому действия выполняем по порядку справа налево.
0 · 2 = 0
0 · 1 = 0
0 · 3 = 0
Если любое число умножить на 0, то получится 0.
Расставим действия.
2 1
8 · (49 − 46) = 24
2 1
3 · (21 − 12) = 27
2 1
7 · (30 − 28) = 14
1 2
40 : 4 · 3 = 30
1 2
50 : 5 · 6 = 60
1 2
70 : 7 · 9 = 90
1 2
1 · 30 : 10 = 3
1 2
1 · 60 : 6 = 10
1 2
1 · 80 : 10 = 8
Вычислим.
8 ∙ (49 – 46) = 24
1) 49 – 46 = 3
2) 8 ∙ 3 = 24
3 ∙ (21 − 12) = 27
1) 21 – 12 = 9
2) 3 ∙ 9 = 27
7 ∙ (30 − 28) = 14
1) 30 – 28 = 2
2) 7 ∙ 2 = 14
40 : 4 ∙ 3 = 30
1) 40 : 4 = 10
2) 10 ∙ 3 = 30
50 : 5 ∙ 6 = 60
1) 50 : 5 = 10
2) 10 ∙ 6 = 60
70 : 7 ∙ 9 = 90
1) 70 : 7= 10
2) 10 ∙ 9 = 90
1 ∙ 30 : 10 = 3
1) 1 ∙ 30 = 30
2) 30 : 10 = 3
1 ∙ 60 : 6 = 10
1)1 ∙ 60 = 60
2) 60 : 6 = 10
1 ∙ 80 : 10 = 8
1) 1 ∙ 80 = 80
2) 80 : 10 = 8
0 ∙ 2 = 0
0 ∙ 1 = 0
0 ∙ 3 = 0
Номер 19.
1) Реши уравнения, подбирая значения х.
2) Вспомни, как можно найти неизвестное слагаемое, уменьшаемое, вычитаемое, и реши уравнения.
1) х ∙ 7 = 21 24 : х = 3
х = 3 х = 8
х ‒ 8 = 0 7 + х = 7
х = 8 х = 0
2)

Уравнение – равенство которое содержит неизвестное число, при подстановке этого числа, получается верное равенство.
Рассуждаем.
х ∙ 7 = 21
Вспомни таблицу умножения на 7. На сколько нужно умножить число, чтобы стало 21. Это число 3, так как 3 · 7 = 21.
х = 3
24 : х = 3
Вспомни таблицу умножения на 3. На сколько нужно умножить 3, чтобы получилось 24. Это число 8, так как 3 · 8 = 24.
х = 8
х – 8 = 0
Какое число нужно прибавить к нулю, чтобы стало 8. Это число 8, так как если к любому числу прибавить нуль, то получим тоже самое число.
х = 8
7 + х = 7
Какое число нужно прибавить к 7, чтобы оно осталось неизменным. Это число 0, так как если к любому числу прибавить нуль, то получим тоже самое число.
х = 0
Рассмотрим уравнения.
38 + x = 50
х – неизвестный множитель, 38 – слагаемое, 50 – сумма.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть второе слагаемое.
x = 50 − 38
x = 12
x − 17 = 20
х – неизвестное уменьшаемое, 17 – вычитаемое, 20 - разность.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
x = 20 + 17
x = 37
40 − x = 19
х – неизвестное вычитаемое, 40 – уменьшаемое, 19 – разность.
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
x = 40 − 19
x = 21
Номер 20.
Используя значения а, заданные на ленте, найди значения выражения: а + 19; а − 19.

а + 19, если а = 27, то 27 + 19 = 46,
а = 31, то 31 + 19 = 50,
а = 52, то 52 + 19 = 71,
а = 64, то 64 + 19 = 83,
а = 70, то 70 + 19 = 89,
а = 79, то 79 + 19 = 98.
а − 19, если а = 27, то 27 − 19 = 8,
а = 31, то 31 − 19 = 12,
а = 52, то 52 − 19 = 33,
а = 64, то 64 − 19 = 45,
а = 70, то 70 − 19 = 51,
а = 79, то 79 − 19 = 60.
1) а + 19 – увеличить число на 19, т.е. к числу прибавить 19.
2) а – 19 – уменьшить число на 19, т.е. из числа вычесть 19.
3) Вычисление значений выражения сводится к применению правил:
Правило прибавления суммы к числу: а + (в + с) = (а + в) + с.
Правило вычитания суммы из числа: а – (в + с) = (а – в) – с.
Увеличим числа на 19.
По правилу прибавления суммы к числу:
27 + 19 = 27 + (16 + 3) = (27 + 3) + 16 = 30 + 16 = 46
Число 19 представим в виде суммы чисел 16 и 3. Сначала к числу 27 прибавим число 3, а потом прибавим число 16.
31 + 19 = 31 + (10 + 9) = (31 + 9) + 10 = 40 + 10 = 50
Число 19 представим в виде суммы чисел 10 и 9. Сначала к числу 31 прибавим число 9, а потом прибавим число 10.
52 + 19 = 52 + (18 + 1) = (52 + 18) + 1 = 70 + 1 = 71
Число 19 представим в виде суммы чисел 18 и 1. Сначала к числу 52 прибавим число 18, а потом прибавим число 1.
64 + 19 = 64 + (16 + 3) = (64 + 16) + 3 = 80 + 3 = 83
Число 19 представим в виде суммы чисел 16 и 3. Сначала к числу 64 прибавим число 16, а потом прибавим число 3.
70 + 19 = 70 + (10 + 9) = (70 + 10) + 9 = 80 + 9 = 89
Число 19 представим в виде суммы чисел 10 и 9. Сначала к числу 70 прибавим число 10, а потом прибавим число 9.
79 + 19 = 79 + (11 + 8) = (79 + 11) + 8 = 90 + 8 = 98
Число 19 представим в виде суммы чисел 11 и 8. Сначала к числу 79 прибавим число 11, а потом прибавим число 8.
По правилу вычитания суммы из числа:
27 − 19 = 27 – (12 + 7) = (27 – 7) – 12 = 20 – 12 = 8
Число 19 разложим на сумму чисел 12 и 7. Сначала из числа 27 вычтем число 7, а потом вычтем число 12.
31 – 19 = 31 – (18 + 1) = (31 – 1) – 18 = 30 – 18 = 12
Число 19 разложим на сумму чисел 18 и 1. Сначала из числа 31 вычтем число 1, а потом вычтем число 18.
52 – 19 = 52 – (12 + 7) = (52 – 12) – 7 = 40 – 7 = 33
Число 19 разложим на сумму чисел 12 и 7. Сначала из числа 52 вычтем число 12, а потом вычтем число 7.
64 – 19 = 64 – (14 + 5) = (64 – 14) – 5 = 50 – 5 = 45
Число 19 разложим на сумму чисел 14 и 5. Сначала из числа 64 вычтем число 14, а потом вычтем число 5.
70 – 19 = 70 – (10 + 9) = (70 – 10) – 9 = 60 – 9 = 51
Число 19 разложим на сумму чисел 10 и 9. Сначала из числа 70 вычтем число 10, а потом вычтем число 9.
79 – 19 = 79 – (10 + 9) = (79 – 9) – 10 = 70 – 10 = 60
Число 19 разложим на сумму чисел 10 и 9. Сначала из числа 79 вычтем число 9, а потом вычтем число 10.
Оформляем задание в тетрадь.
а + 19, если:
а = 27, то 27 + 19 = 46
а = 31, то 31 + 19 = 50
а = 52, то 52 + 19 = 71
а = 64, то 64 + 19 = 83
а = 70, то 70 + 19 = 89
а = 79, то 79 + 19 = 98
а − 19, если:
а = 27, то 27 − 19 = 8
а = 31, то 31 − 19 = 12
а = 52, то 52 − 19 = 33
а = 64, то 64 − 19 = 45
а = 70, то 70 − 19 = 51
а = 79, то 79 − 19 = 60
Номер 21.
Ответ:
1) Помни, единицы можно складывать и вычитать только с единицами, десятки – с десятками.
2) 1 дес. = 10 ед.
Рассуждаем.
56 + 39.
Складываем единицы. 6 + 9 = 15 – получилось 1 дес. и 5 ед.
Записываем в разряде единиц число 5, а 1 дес. запоминаем.
Складываем десятки. 5 + 3 = 8 и ещё 1 дес., который запомнили 8 + 1 = 9 – получилось десятков.
Записываем в разряде десятков число 9.
Читаем ответ: 95.
73 + 26.
Складываем единицы. 3 + 6 = 9 – получилось 9 ед.
Записываем в разряде единиц число 9.
Складываем десятки. 7 + 2 = 9 – получилось десятков.
Записываем в разряде десятков число 9.
Читаем ответ: 99.
34 + 66.
Складываем единицы. 4 + 6 = 10 – получилось 1 дес. и 0 ед.
Записываем в разряде единиц число 0, а 1 дес. запоминаем.
Складываем десятки. 3 + 6 = 9 и ещё 1 дес., который запомнили 9 + 1 = 10 – получилось десятков.
10 дес. = 1 сот. и 0 дес.
Записываем в разряде десятков число 0.
Записываем в разряде сотен число 1.
Читаем ответ: 100.
87 – 38.
Вычитаем единицы. От числа 7 мы не можем отнять 8.
Занимаем 1 дес. = 10 ед., 10 + 7 = 17 ед., 17 – 8 = 9 – получилось единиц.
Записываем в разряде единиц число 9.
Вычитаем десятки. Было 8 дес., мы занимали 1 дес, осталось 8 – 1 = 7 дес.,
7 – 3 = 4 – получилось десятков.
Записываем в разряде десятков число 4.
Читаем ответ: 49.
63 + 19.
Складываем единицы. 3 + 9 = 12 – получилось 1 дес. и 2 ед.
Записываем в разряде единиц число 2, а 1 дес. запоминаем.
Складываем десятки. 6 + 1 = 7 и ещё 1 дес., который запомнили 7 + 1 = 8 – получилось десятков.
Записываем в разряде десятков число 8.
Читаем ответ: 82.
Запишем вычисление в столбик в тетрадь.
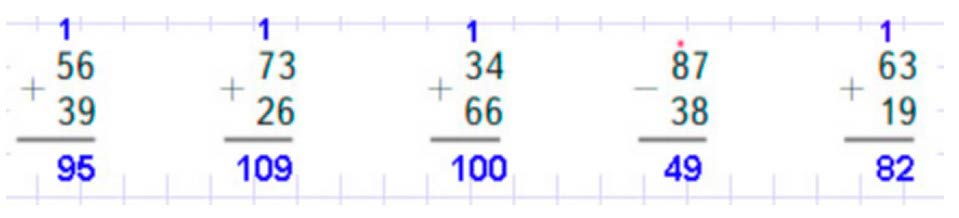
Номер 22.
1) Найди периметр прямоугольника, длины сторон которого 8 дм и 6 дм.
2) Найди периметр треугольника, каждая сторона которого имеет длину 7 см.
1-й способ решения:
1) (8 + 6) ∙ 2 = 28 дм.
Ответ: периметр прямоугольника 28 дм.
2) 7 ∙ 3 = 21 см.
Ответ: периметр треугольника 21 см.
2-й способ решения:
1) 8 ∙ 2 + 6∙ 2 = 8 + 8 + 6 + 6 = 28 (дм) – периметр прямоугольника.
Ответ: 28 дм.
2) 7 + 7 + 7 = 21 (см) – периметр треугольника.
Ответ: 21 см.
1) Периметр – это сумма длин всех сторон.
2) вспомни, чтобы вычислить периметр многоугольника нужно сложить все его стороны.
Размышляем.
Многоугольник – замкнутая ломаная.
Из-за того, что многоугольник – замкнутая ломаная, то периметр многоугольника равен длине ломаной. А раз длина ломаной – сумма длин все отрезков-звеньев, то периметр многоугольник – сумма длин всех его сторон.
Вспомним формулы вычисления периметра прямоугольника:
1) а + b + a + b
2) a · 2 + b · 2
3) (a + b) · 2
Где а и b – это стороны прямоугольника.
Вспомним формулу треугольника, у которого все стороны равны:
а + а + а = а · 3
Так как у такого треугольника все стороны равны, то сложение одинаковых слагаемых можно заменить умножением, то есть длину стороны умножить на количество сторон.
Вычислим периметр прямуогольника ОРТN.

1 способ: 8 + 6 + 8 + 6 = 14 + 14 = 28 (см)
2 способ: 8 · 2 + 6 · 2 = 16 + 12 = 28 (см)
3 способ: (8 + 6) · 2 = 14 · 2 = 28 (см)
Вычислим периметр треугольник KLM.

7 + 7 + 7 = 7 · 3 = 21 (см)
Задание на полях страницы
Найди лишнее выражение:

Ответ:
20 + 28 = 48 40 + 8 = 48 24 + 24 = 48 30 + 18 = 48 15 + 34 = 49 – лишнее выражение 60 − 12 = 48 Пояснение: лишнее выражение 15 + 34 = 49, потому что значение этого выражения отличается от остальных.
Чтобы узнать, какое выражение лишнее, нужно сравнить все выражения: из каких компонентов состоит, на каком действии основано и какое значение выражения.
Вычислим выражения.
20 + 28 = (20 + 20) + (0 + 8) = 40 + 8 = 48
Сложим по разрядам: единицы с единицами, а десятки с десятками.
40 + 8 = 48
Сложим по разрядам: единицы с единицами, а десятки с десятками.
24 + 24 = (20 + 20) + (4 + 4) = 40 + 8 = 48
Сложим по разрядам: единицы с единицами, а десятки с десятками.
30 + 18 = (30 + 10) + 8 = 40 + 8 = 48
Сложим по разрядам: единицы с единицами, а десятки с десятками.
15 + 34 = (10 + 30) + (5 + 4) = 40 + 9 = 49
Сложим по разрядам: единицы с единицами, а десятки с десятками.
60 – 12 = 60 – (10 + 2) = (60 – 10) – 2 = 50 – 2 = 48
Разложим число 12 на сумму чисел 10 и 2. Сначала из числа 60 вычтем число 10, а потом вычтем число 2.
Делаем вывод.
Таким образом, лишнее выражение – это 15 + 34, потому что отличается значением, у данного выражения значение равно 49, а у других выражений – 48.
15 + 34 – лишнее выражение.
Задание внизу страницы
Вариант 2
Выбери правильный ответ.
Номер 1.
Какое число надо записать в окошко, чтобы стало верным равенство 18 + 18 + 18 = ⬜ · 3
Варианты ответов:
4 18 3
Ответ: 18
Пояснение: в окошко нужно записать число 18, потому что 18 + 18 + 18 = 18 · 3
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
Чтобы равенство стало верным, нужно 18 взять 3 раза, поэтому верная запись 18 · 3.
Выбираем правильный ответ.
Ответ: 18.
Номер 2.
Какой знак арифметического действия надо записать в кружок, чтобы равенство 13 · 4 = 4 ◯ 13 стало верным?
Варианты ответов:
«+» «=» «·» «:»
Ответ: «·»
Пояснение: в окошко нужно записать знак «·», потому что от перестановки мест множителей значение произведения не изменяется.
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
Чтобы равенство стало верным, применим закон «от перестановки мест множителей произведение не изменяется».
Выбираем правильный ответ.
Ответ: « · »
Номер 3.
Укажи произведение чисел 8 и 3.
Варианты ответов:
32 16 24
Ответ: 24
Пояснение: произведение чисел 8 и 3 равно 24, потому что 8 · 3 = 24
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
Чтобы найти произведение данных чисел, их нужно умножить, значит, 8 · 3 = 24.
Выбираем правильный ответ.
Ответ: 24.
Номер 4.
Укажи частное чисел 18 и 9.
Варианты ответов:
2 3 9
Ответ: 2
Пояснение: частное числе 18 и 9 равно 2, потому что 18 : 9 = 2
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
Чтобы найти частное данных чисел, их нужно разделить, значит, 18 : 9 = 2.
Выбираем правильный ответ.
Ответ: 2.
Номер 5.
Какое число надо записать в окошко, чтобы равенство 12 : 2 = ⬜ : 3 стало верным?
Варианты ответов:
15 18 6
Ответ: 18
Пояснение: в окошко нужно записать число 18, потому что 12 : 2 = 18 : 3
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
12 : 2 = 6, вспомним таблицу умножения, какое число нужно разделить на 3, чтобы получить 6. Это число 18. Значит, 18 : 3 = 6.
Выбираем правильный ответ.
Ответ: 18.
Номер 6.
Какой знак действия надо записать в кружок, чтобы получить верное равенство? 4 · 2 = 16 ◯ 2
Варианты ответов:
«+» «·» «-» «:»
Ответ: «:»
Пояснение: в окошко нужно записать знак «:», потому что 4 · 2 = 16 : 2
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
4 · 2 = 8, вспомним, что 16 : 2 тоже равно 8, значит нужно поставить знак « : », чтобы равенство было верным.
Выбираем правильный ответ.
Ответ: « : ».
Номер 7.
В каком варианте ответа порядок действий указан правильно?
Варианты ответов:

Ответ: Второй вариант
Пояснение: верный порядок действий указан во втором выражении. потому что сначала выполняется действие вычитания в скобках, затем умножение и вычитание.
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
Чтобы правильно ответить на данный вопрос, вспомним правило: сначала действие в скобках, потом умножение и деление и только потом сложение и вычитание. Значит, правильный ответ во втором примере.
Выбираем правильный ответ.
Ответ: во втором.
Номер 8.
Укажи верное значение числового выражения 27 – (15 + 12) : 3
Варианты ответов:
18 8 10
Ответ: 18
Пояснение: верное значение выражения 27 – (25 + 12) : 3 = 27 – 27 : 3 = 27 – 9 = 18
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
Вспомним правило: сначала действие в скобках, потом умножение и деление и только потом сложение и вычитание.
Решим пример:
27 – (15 + 12) : 3 = 18
1) 15 + 12 = 27
2) 27 : 3 = 9
3) 27 – 9 = 18
Выбираем правильный ответ.
Ответ: 18.
Номер 9.
Каким действием решается задача? Выбери знак.
«18 кубиков разложили в несколько коробок, по 6 кубиков в каждую. Сколько коробок заняли эти кубики?»
Варианты ответов:
«+» «·» «-» «:»
Ответ: Делением «:»
Пояснение: задача решается делением, потому что 18 : 6 = 3 (к.) - заняли эти кубики.
Вспомним порядок выполнения действий и повторим названия чисел при умножении и делении, а так же, чем равенство отличается от неравенства.
Рассуждаем.
В задаче говорится, что кубики разложили по шесть штук в несколько коробок, значит знак будет « : ».
18 : 6 = 3
Выбираем правильный ответ.
Ответ: делением « : ».
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.