Вход

Математика 2 класс учебник Моро, Волкова 1 часть ответы – страница 9

  • Тип: ГДЗ, Решебник.
  • Авторы: Моро М. И., Волкова С. И., Степанова С. В.
  • Часть: 1.
  • Год: 2020-2024.
  • Серия: Школа России (ФГОС).
  • Издательство: Просвещение.
alt
Автор
Материал подготовила:
Ольга Дмитриева
математика 2 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 9

Номер 1.

Выпиши в одну строку однозначные числа, а в другую – двузначные числа:

Ответ:

7, 2, 1, 9. 15, 51, 70, 13, 10, 99.

Подсказка:

Однозначные числа – числа, в записи которых один знак.
Двузначные числа – числа, в записи которых два знака.

Шаг 1.
Рассуждаем

Найдем все числа, в записи которых один знак.
7, 2, 1, 9- это однозначные числа.

Шаг 2.
Продолжаем рассуждение

Найдем все числа, в записи которых два знака.
15, 51, 70, 13, 10, 99 - это двузначные числа.

Номер 2.

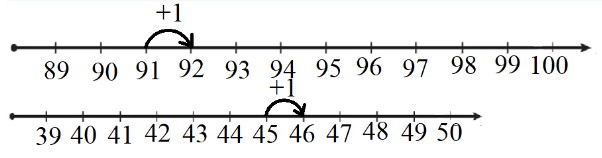
Какие числа пропущены в каждом ряду?

Ответ:

41, 43, 44, 46, 47, 49, 51. 90, 92, 93, 95, 97, 99, 100.

Подсказка:

Вспомни числовой луч, чтобы вставить пропущенные числа.

Пояснение к заданию 2
Шаг 1.
Рассуждаем

Вспомним свойства ряда натуральных чисел. Ряд натуральных чисел составлен так, что каждое следующее число на 1 больше предыдущего.

Шаг 2.
Продолжаем рассуждение

Вставим пропущенные числа по порядку.
41, 43, 44, 46, 47, 49, 51.
90, 92, 93, 95, 97, 99, 100.

Номер 3.

Ответ:

16 < 60    2 дм > 12 см    24 < 42 90 > 19    7 дм = 70 см    65 > 56

Подсказка:

Не забудь проверить единицы измерения в двух последних выражениях, потому что при сравнении они должны быть одинаковыми.

Шаг 1.
Рассуждаем

Вспомним расположение данных чисел на числовом луче. То, что стоит на числовом луче правее – больше, а то, что левее – меньше.

Шаг 2.
Расставим знаки >, < или =

16 < 60

90 > 19

2 дм > 12 см
20 см> 12 см

7 дм = 70 см
70 см= 70 см

24 < 42

65 > 56

Номер 4.

Отличается задание? Переключите год учебника.
Переключение года издания

Миша выиграл 6 партий в шашки, а Ваня – на 2 партии больше. Поставь вопрос и реши задачу.

Ответ:

Сколько партий выиграл Ваня?
математика 2 класс Моро, Волкова, Бантова, Бельтюкова - 1 часть страница 9. Номер 4
1) 6 + 2 = 8 (п.) – выиграл Ваня Ответ: 8 партий выиграл Вана в шашки.

Подсказка:

Для оформления условий задачи выполняем краткую запись.

Шаг 1.
Рассуждаем

Нам известно, что Миша выиграл 6 партий в шашки, а сколько выиграл Ваня нам не известно, сказано только, что он выиграл на две партии больше, чем Миша. Поэтому вопрос можно поставить такой: «Сколько партий выиграл Ваня?».

Шаг 2.
Оформляем условие в виде краткой записи.
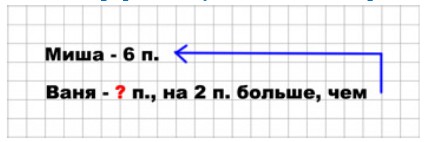
Пояснение к заданию 4

Шаг 3.
Продолжаем рассуждение

Чтобы узнать, сколько партий выиграл Ваня, нам нужно к количеству выигранных партий Мишей прибавить число 2.
6 + 2 = 8 (п) - выиграл Ваня

Шаг 4.
Записываем ответ

Ответ: 8 партий

В школьном турнире Миша выиграл 6 партий в шашки, а Ваня – на 2 партии больше. Задай вопрос и реши задачу.

Ответ:

Сколько партий сыграли мальчики всего?
Миша - 6 п. Ваня - ? п., на 2 п. больше.
1) 6 + 2 = 8 (п.) - сыграл Ваня. 2) 6 + 8 = 14 (п.) - сыграли мальчики всего. Ответ: 14 партий сыграли мальчики всего.

Подсказка:

Повторим состав числа 8 и случаи табличного сложения, а также вспомним, что значит на 2 больше.

Шаг 1.
Задаем вопрос к условию задачи

Сколько партий сыграли мальчики всего?

Шаг 2.
Оформляем условие задачи в виде краткой записи

Миша - 6 п.
Ваня - ? п., на 2 п. больше.
Всего - ? п.

Шаг 3.
Рассуждаем

Чтобы узнать, сколько партий выиграл Ваня, нам нужно к количеству выигранных партий Мишей прибавить число 2.
1) 6 + 2 = 8 (п) - выиграл Ваня

Шаг 4.
Продолжаем рассуждение

Чтобы узнать, сколько партий было сыграно всего, нужно сложить количество побед Вани и Миши вместе.
2) 6 + 8 = 14 (п.) - сыграли мальчики всего.

Шаг 5.
Записываем ответ

Ответ: 14 партий.

Номер 5.

Отличается задание? Переключите год учебника.
Переключение года издания

1) У Коли было 6 книг. В день рождения ему подарили еще 4 книги. Сколько книг стало у Коли?
2) У Коли 10 книг. Он отнес 2 книги в классную библиотеку. Сколько книг у него осталось?

Ответ:

Задача 1: Было – 6 кн. Подарили – 4 кн. Стало – ? 6 + 4 = 10 (к.) – у Коли. Ответ: 10 книг стало у Коли всего.
Задача 2: Было – 10 кн. Отнёс – 2 кн. Осталось – ? 10 − 2 = 8 (к.) – у Коли. Ответ: 8 книг осталось у Коли всего.

Подсказка:

Для оформления условий задач выполняем краткую запись.

Шаг 1.
Оформляем условие 1-й задачи в виде краткой записи.
Пояснение к заданию 5

Шаг 2.
Продолжаем рассуждение

Чтобы узнать, сколько книг стало у Коли, нужно к количеству книг, которые были прибавить книги, которые ему подарили.
6 + 4 = 10 (к) – стало у Коли

Шаг 3.
Записываем ответ

Ответ: 10 книг

Шаг 4.
Оформляем условие 2-й задачи в виде краткой записи.
Пояснение к заданию 5

Шаг 5.
Продолжаем рассуждение

Чтобы узнать, сколько книг осталось у Коли, нужно из общего количества книг вычесть 2 книги, которые он отнес в библиотеку.
10 - 2 = 8 (к) – осталось у Коли

Шаг 6.
Записываем ответ

Ответ: 8 книг

У Коли было 6 книг. В день рождения ему подарили еще 4 книги. Он отнес 2 книги в классную библиотеку. Сколько книг у него осталось? Запиши в каждом решении первое действие, если вторым было:
2) 4 + 4 = 8 (кн.) Ответ: 8 книг.
2) 10 – 2 = 8 (кн.) Ответ: 8 книг.
2) 6 + 2 = 8 (кн.) Ответ: 8 книг.

Ответ:

Было – 6 кн. Подарили – 4 кн. Отнес – 2 кн. Осталось - ? кн.
Решение 1: 1) 6 – 2 = 4 (кн.) – осталось у Коли, после того, как он отнес книги в библиотеку. 2) 4 + 4 = 8 (кн.) – осталось у Коли. Ответ: 8 книг осталось у Коли всего.
Решение 2: 1) 6 + 4 = 10 (кн.) – стало у Коли. 2) 10 – 2 = 8 (кн.) – осталось у коли. Ответ: 8 книг осталось у Коли всего.
Решение 3: 1) 4 – 2 = 2 (кн.) – осталось от подаренных. 2) 6 + 2 = 8 (кн.) – осталось всего. Ответ: 8 книг осталось у Коли всего.

Подсказка:

Состав любого числа – это пара любых слагаемых, которые в сумме дают этот результат. Например, число 10 можно получить как 5 + 5, как 3 + 7, как 1 + 9 и т.д.

Шаг 1.
Оформляем условие задачи в виде краткой записи

Было – 6 кн.
Подарили – 4 кн.
Отнес – 2 кн.
Осталось - ? кн.

Шаг 2.
Дополняем решение № 1

Узнаем, сколько книг осталось у Коли после того как он отнес 2 в библиотеку. Для этого из количества книг, которые были у Коли, вычитаем 2.
1) 6 – 2 = 4 (кн.) – осталось у Коли, после того, как он отнес книги в библиотеку.
2) 4 + 4 = 8 (кн.) – осталось у Коли.
Ответ: 8 книг.

Шаг 3.
Дополняем решение № 2

Узнаем, сколько книг стало у Коли, после того как ему подарили 4 книги. Для этого к количеству книг, которые у него были, прибавляем 4.
1) 6 + 4 = 10 (кн.) – стало у Коли.
2) 10 – 2 = 8 (кн.) – осталось у коли.
Ответ: 8 книг.

Шаг 4.
Дополняем решение № 3

Узнаем, сколько книг осталось у Коли, если 2 из 4 подаренных он отнес в библиотеку.
1) 4 – 2 = 2 (кн.) – осталось от подаренных.
2) 6 + 2 = 8 (кн.) – осталось всего.
Ответ: 8 книг.

Номер 6.

Ответ:

11 – 8 = 3      17 – 9 = 8    6 + 6 = 12 11 – 9 = 2      17 – 8 = 9    5 + 6 = 11
18 – 10 = 8    70 – 30 = 40 13 – 10 = 3    80 – 20 = 60

Подсказка:

Правило вычитания суммы из числа: а – (в + с) = (а – с) – в
Правило вычитания числа из суммы: (а + в) – с = (а – с) + в
Правило прибавления суммы к числу: а + (в + с) = (а + в) + с

Шаг 1.
Выполним вычисления

11 – 8 = 11 – (1 + 7) = (11 – 1) – 7 = 10 – 7 = 3
11 – 9 = 11 – (1 + 8) = (11 – 1) – 8 = 10 – 8 = 2
17 – 9 = 17 – (7 + 2) = (17 – 7) – 2 = 10 – 2 = 8
17 – 8 = 17 – (7 + 1) = (17 – 7) – 1 = 10 – 1 = 9
6 + 6 = 6 + (4 + 2) = (6 + 4) + 2 = 10 + 2 = 12
5 + 6 = 5 + (5 + 1) = (5 + 5) + 1 = 10 + 1 = 11
18 – 10 = (10 + 8) – 10 = (10 – 10) + 8 = 0 + 8 = 8
13 – 10 = (10 + 3) – 10 = (10 – 10) + 3 = 0 + 3 = 3
70 – 30 = 7 дес. – 3 дес. = 4 дес. = 40
80 – 20 = 8 дес. – 2 дес. = 6 дес. = 60

Номер 7.

Сколькими способами можно составить набор из двух овощей? Зарисуй эти наборы в тетради.

Ответ:

Свекла – с., морковь – м., огурец – о., помидор – п. С + м; с + о; с + п; м + о; м + п; о + п. 6 наборов.

Подсказка:

В математике существует способ, который помогает быстро решить задачу такого типа. Прием называется составления «дерево возможностей»

Шаг 1.
Рассуждаем

Дерево возможностей составляется так:
Первый ряд – первый овощ в паре. Первым может быть каждый из овощей.
Второй ряд – возможные пары овощей. Пару могут образовывать только отличные овощи, при этом сочетания типа свекла-помидор и помидор - свекла исключают друг друга.
Таким образом, рассуждая, составляем дерево, из которого видно, что свекла может образовывать набор с тремя овощами; морковь с двумя, а огурец – с одним.

Шаг 2.
Запишем и зарисуем данные наборы

Свекла – с., морковь – м., огурец – о., помидор – п.
С + м; с + о; с + п; м + о; м + п; о + п.
6 наборов.

Пояснение к заданию 7

Задание на полях страницы

Ребусы:

Ответ:

99 + 1 = 100 39 + 1 = 40 80 − 1 = 79 89 + 1 = 90

Подсказка:

Ре́бус — загадка, в которой разгадываемые слова даны в виде рисунков в сочетании с буквами, цифрами и другими знаками.

Шаг 1.
Рассуждаем

В первом ребусе нам видно, что к двузначному числу прибавили однозначное и получили трехзначное. Значит, нужно взять самое большое двузначное число и прибавить к нему однозначное, подбором, начиная с самого маленького, то есть с единицы.
99 + 1 = 100

Шаг 2.
Продолжаем рассуждение

Чтобы узнать, какое число пропущено во втором ребусе, нужно выполнить проверку, то есть из суммы вычесть известное слагаемое (40 - 39 = 1).
39 + 1 = 40

Шаг 3.
Продолжаем рассуждение

Чтобы узнать, какое число пропущено в третьем ребусе, нужно выполнить проверку, то есть к разности прибавить вычитаемое (79 + 1 = 80).
80 − 1 = 79

Шаг 4.
Продолжаем рассуждение

Чтобы узнать, какое число пропущено в четвертом ребусе, нужно выполнить проверку, то из суммы вычесть известное слагаемое (90 - 1 = 89).
89 + 1 = 90

Задание внизу страницы

Проверочные работы с.4 Проверочные работы с.5

Конец страницы
Переход на другие страницы Содержание
Информация на этой странице была полезной?
★★★★★
0/5 (0 голосов)
Нашли ошибку на сайте? Помогите нам ее исправить!
Сообщить об ошибке

С подпиской рекламы не будет

Подключите премиум подписку со скидкой в 40% за 149 ₽
Подключить
Понравились решения?
Напишите свой комментарий.