Математика 2 класс учебник Моро, Волкова 1 часть ответы – страница 15

- Тип: ГДЗ, Решебник.
- Авторы: Моро М. И., Волкова С. И., Степанова С. В.
- Часть: 1.
- Год: 2020-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Задание вверху страницы
Ответ:15 = 10 + 5 37 = 30 + 7 56 = 50 + 6 28 = 20 + 8 84 = 80 + 4 65 = 60 + 5
Разрядные слагаемые - это сложение чисел с разной разрядностью. Например, цифры от 1 до 9 - это "единицы", цифры 10,20, 30 - "десятки", и т. д.
Соответственно, если суммировать единицы и десятки, то каждое из слагаемых будет разрядным.
Выполним вычисления
Представим числа в виде разрядных слагаемых.
15 = 10 + 5
28 = 20 + 8
37 = 30 + 7
84 = 80 + 4
56 = 50 + 6
65 = 60 + 5
Номер 1.
Ответ:59 – 9 = 50 8 + 40 = 48 83 – 80 = 3 90 + 6 = 96 66 – 60 = 6 97 – 7 = 90
Десятки можно вычитать только из десятков, а единицы из единиц.
Выполним вычисления
59 – 9 = 5 дес.9ед. – 9 ед. = 5 дес. = 50
8 + 40 = 8 ед. + 4 дес. = 4 дес.8ед. = 48
83 – 80 = 8 дес.3ед. – 8 дес. = 3 ед. = 3
90 + 6 = 9 дес. + 6 ед. = 9дес.6ед. = 96
66 – 60 = 6дес.6ед. – 6 дес. = 6 ед.= 6
97 – 7 = 9 дес.7ед. – 7 ед. = 9 дес. = 90
Оформляем задание в тетрадь
59 – 9 = 50
8 + 40 = 48
83 – 80 = 3
90 + 6 = 96
66 – 60 = 6
97 – 7 = 90
Номер 2.
Назови пропущенные единицы длины:
Ответ:1) Ширина стола – 60 см; 2) Высота стула – 4 дм; 3) Толщина стекла – 5 мм.
1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 км = 1000 м
Оформляем задание в тетрадь
1) Ширина стола – 60 см;
2) Высота стула – 4 дм;
3) Толщина стекла – 5 мм.
Номер 3.
К шлангу длиной 5 м присоединили с одной стороны шланг длиной 3 м, а с другой – шланг длиной 2 м. Какой длины стал шланг?
Ответ:1) 3 + 2 = 5 (м) – добавили к шлангу. 2) 5 + 5 = 10 (м) – стала длина шланга. Ответ: шланг стал длиной 10 метров.
Для оформления условий задачи выполняем краткую запись.
Оформляем условие задачи в виде краткой записи.

Рассуждаем
Для начала нам нужно узнать, сколько метров шланга добавили к шлангу длиной 5 метров. Для этого мы складываем длину шланга, который присоединили с одной стороны с длиной шланга, присоединенного с другой стороны.
3 + 2 = 5 (м) - добавили к шлангу
Продолжаем рассуждение
Чтобы узнать, какой длины стал шланг, необходимо к его начальной длине прибавить количество метров, которые к нему добавили.
5 + 5 = 10 (м) - стала длина шланга
Записываем ответ
Ответ: 10 метров.
Номер 4.
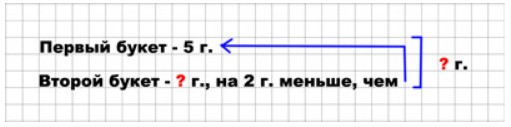
В одном букете 5 гвоздик, а в другом – на 2 гвоздики меньше. Сколько всего гвоздик в этих букетах?
Выбери решение этой задачи.
Составь задачу по другому решению.

1) 5 – 2 = 3 (г.) – во втором букете.
2) 5 + 3 = 8 (г.) – в двух букетах.
Ответ: 8 гвоздик в двух букетах всего.
Значит, верное решение задачи - 2.
Задача по решению 1:
В одном букете 5 гвоздик, а в другом – на 2 гвоздики больше. Сколько всего гвоздик в этих букетах?
Для оформления условий задачи выполняем краткую запись.
Оформляем условие задачи в виде краткой записи.
Рассуждаем
Для того чтобы узнать сколько гвоздик во втором букете, нужно из количества гвоздик первого букета вычесть 2.
5 - 2 = 3 (г) – во втором букете
Продолжаем рассуждение
Чтобы узнать, сколько всего гвоздик в двух букетах, нужно сложить количество гвоздик первого и второго букетов.
5 + 3 = 8 (г) - в двух букетах
Записываем ответ
Ответ: 8 гвоздик
Делаем вывод
Значит, верное решение задачи - 2
Составляем задачу
Задача по решению 1 будет следующая.
В одном букете 5 гвоздик, а в другом – на 2 гвоздики больше. Сколько всего гвоздик в этих букетах?
Номер 5.
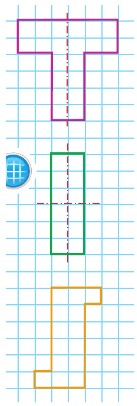
Начерти и вырежи такие фигуры.
1)Перегни фигуру 1 по красной линии. Фигура разделилась на 2 одинаковые части, которые совпали друг с другом. Такую фигуру называют симметричной, а линию сгиба называют осью симметрии фигуры.
2) У прямоугольника (рис. 2) две оси симметрии. Проверь это.
3) Что можно сказать о фигуре 3? Она симметричная?
1) Проверили, что если перегнуть фигуру 1 по красной линии, то тогда фигура разделилась на 2 одинаковые части, которые совпали друг с другом. Таким образом мы получили ось симметрии.
2) У прямоугольника (рис. 2) две оси симметрии. Проверим это путём сложения фигуры.
3) Фигура под номером 3 не является симметричной, такие фигуры называют асимметричными.
Рассуждаем
Начертим и вырежем данные фигуры.
Продолжаем рассуждение
Перегни фигуру 1 по красной линии. Фигура разделилась на 2 одинаковые части, которые совпали друг с другом.
Такую фигуру называют симметричной, а линию сгиба называют осью симметрии фигуры.
Продолжаем рассуждение
У прямоугольника (рис.2) две оси симметрии.
Продолжаем рассуждение
Фигура под номером 3 не является симметричной, такие фигуры называют асимметричными.
Задание внизу страницы
Ответ:64 − 60 + 8 = 12 50 − 1 − 40 = 9 97 − 7 − 90 = 0
Правило вычитания числа из суммы: (а + в) – с = (а – с) + в
Выполним вычисления
64 − 60 + 8 = (60 + 4) – 60 + 8 = (60 – 60) + (4 + 8) = 0 + 12 = 12
50 − 1 − 40 = (50 – 40) – 1 = 10 – 1 = 9
97 − 7 − 90 = (90 + 7) – 7 – 90 = 0
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽






Напишите свой комментарий.