Алгебра 9 класс учебник Макарычев, Миндюк ответы – номер 619

Учебник по алгебре 9 класс. Авторы: Макарычев, Миндюк, Нешков.

Тип: ГДЗ, Решебник.
Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
Часть: без частей.
Год: 2023-2025.

Серия: Школа России (ФГОС).
Издательство: Просвещение.

Автор

Материал подготовила:

Екатерина Шамрай

Номер 619.

Найдите сумму первых n членов геометрической прогрессии:

а) 1; 2; 3²; ... ;
б) 2; 2²; 2³; ... ;
в) 1/2; –1/4; 1/8; ... ;
г) 1; –х; х²; ..., где х ≠ –1;
д) 1; х²; х⁴; ..., где х ≠ ± 1;
е) 1; –х³; х⁶; ..., где х ≠ –1.

Ответ:

а) 1; 2; 3²; ...
C₁ = 1; q = 3 : 1 = 3

S_n = $$\frac{c_1(q^n - 1)}{q - 1}$$

S₉ = $$\frac{1 · (3^n - 1)}{3 - 1}$$ = $$\frac{3^n - 1}{2}$$

б) 2; 2²; 2³; …
C₁ = 2; q = 2² : 2 = 2

S_n = $$\frac{c_1(q^n - 1)}{q - 1}$$

S₉ = $$\frac{2 · (2^n - 1)}{2 - 1}$$ = 2 · (2ⁿ – 1)

в) 1/2; –1/4; 1/8; ... ;

C₁ = 1/2; q = –1/4 : 1/2 = –1/2

S_n = $$\frac{c_1(q^n - 1)}{q - 1}$$

S₉ =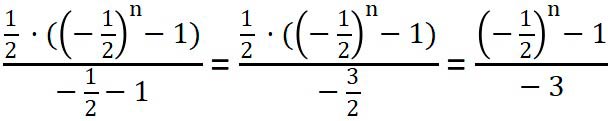

г) 1; –x; x²; …
C₁ = 1; q = –x : 1 = –x

S_n = $$\frac{c_1(q^n - 1)}{q - 1}$$

S₉ = $$\frac{1 · ((-x)^n - 1)}{-x - 1}$$ = $$\frac{(-x)^n - 1}{-x - 1}$$

д) 1; x²; x⁴; …
C₁ = 1; q = x² : 1 = x²

S_n = $$\frac{c_1(q^n - 1)}{q - 1}$$

S₉ = $$\frac{1 · ((-x^2)^n - 1)}{x^2 - 1}$$ = $$\frac{x^2{^n} - 1}{x^2 - 1}$$

е) 1; –x³; x⁶; …
C₁ = 1; q = –x³ : 1 = –x³

S_n = $$\frac{c_1(q^n - 1)}{q - 1}$$

S₉ = $$\frac{1 · ((-x^3)^n - 1)}{-x^3 - 1}$$ = $$\frac{(-x)^3{^n} - 1}{-x^3 - 1}$$