Алгебра 9 класс учебник Макарычев, Миндюк ответы – номер 612

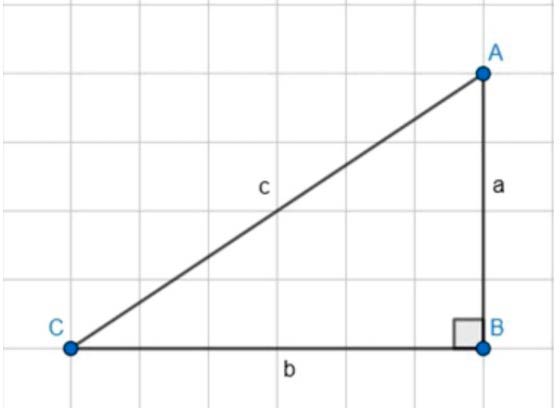
Пусть a = b₁, b = b₂, c = b
b₁
b₂ = b₁q
b₃ = b₁q²

Тогда по теореме Пифагора
a² + b² = c²
b₁² + (b₁q)² = (b₁q²)²
b₁² + b₁²q² = b₁²q⁴ | : b₁², b₁ ≠ 0
1 + q² = q⁴
q⁴ – q² – 1 = 0

Введем новую переменную
q² = t, t ≥ 0
t² – t – 1 = 0
D = (–1)² – 4(–1) = 5

t₁ = $$\frac{1 + \sqrt{5}}{2}$$

t₂ = $$\frac{1 - \sqrt{5}}{2}$$ < 0
t₂ – не подходит

q² = $$\frac{1 + \sqrt{5}}{2}$$

q = $$\sqrt\frac{1 + \sqrt{5}}{2}$$

q = –$$\sqrt\frac{1 + \sqrt{5}}{2}$$ < 0
не подходит

Значит, если стороны прямоугольного треугольника будут равны

b₁, b₁$$\sqrt\frac{1 + \sqrt{5}}{2}$$, b₁($$\sqrt\frac{1 + \sqrt{5}}{2}$$)² = b₁$$\frac{1 + \sqrt{5}}{2}$$

То длины сторон этого треугольника будут составлять геометрическую прогрессию

Проверка

a = 1, b = $$\sqrt\frac{1 + \sqrt{5}}{2}$$, c = $$\frac{1 + \sqrt{5}}{2}$$

a² + b² = 1 + ($$\sqrt\frac{1 + \sqrt{5}}{2}$$)² = $$\frac{2 + 1 + \sqrt{5}}{2}$$ = $$\frac{3 + \sqrt{5}}{2}$$

c² = ($$\sqrt\frac{1 + \sqrt{5}}{2}$$)² = $$\frac{1 + 2\sqrt{5} + 5}{4}$$ = $$\frac{6 + 2\sqrt{5}}{4}$$ = $$\frac{3 + \sqrt{5}}{2}$$ = a² + b²