Алгебра 9 класс учебник Макарычев, Миндюк ответы – номер 333

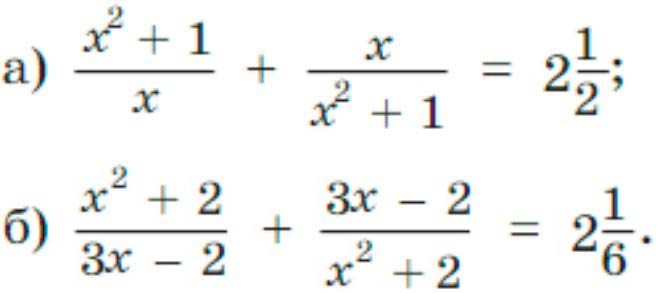
а) $$\frac{х^2 + 1}{х}$$ + $$\frac{х}{х^2 + 1}$$ = 21/2

Пусть t = $$\frac{х^2 + 1}{х}$$, x ≠ 0

t + 1/t = 21/2

2t² + 2 = 5t
2t² – 5t + 2 = 0
D = (–5)² – 4 · 2 · 2 = 25 – 16 = 9

t = $$\frac{5 ± \sqrt{9}}{2 \cdot 2}$$ = 5 ± 3/4

t₁ = 2
t₂ = 1/2

$$\frac{х^2 + 1}{х}$$ = 2    или    $$\frac{х^2 + 1}{х}$$ = 1/2
х² + 1 = 2х               2(х² + 1) = х
х² – 2х + 1 = 0         2х² + 2 – х = 0
(х – 1)² = 0               D = (–1)² – 4 · 2 · 2 = –15
х = 1                          корней нет

Ответ: 1

б) $$\frac{х^2 + 2}{3х - 2}$$ + $$\frac{3х - 2}{х^2 + 2}$$ = 21/6

3х – 2 ≠ 0
3х ≠ 2
х ≠ 2/3

Пусть t = $$\frac{х^2 + 2}{3х - 2}$$

t + 1/t = 13/6

6t² + 6 = 13t
6t² – 13t + 6 = 0
D = (–13)² – 4 · 6 · 6 = 169 – 144 = 25

t = $$\frac{13 ± \sqrt{25}}{2 \cdot 6}$$ = 13 ± 5/12

t₁ = 18/12 = 3/2
t₂ = 8/12 = 2/3

$$\frac{х^2 + 2}{3х - 2}$$ = 3/2        или          $$\frac{х^2 + 2}{3х - 2}$$ = 2/3
2(х² + 2) = 3(3х – 2)             3(х² + 2) = 2(3х – 2)

2х² + 4 = 9х – 6                    3х² + 6 = 6х – 4
2х² – 9х + 10 = 0                  3х² – 6х + 10 = 0
D = (–9)² – 4 · 2 · 10 = 1       D₁ = (–3)² – 3 · 10 = –21

x = $$\frac{9 ± \sqrt{1}}{2 \cdot 2}$$ = 9 ± 1/4            корней нет
x₁ = 2, x₂ = 10/4 = 2,5

Ответ: 2 и 2,5