Алгебра 9 класс учебник Макарычев, Миндюк ответы – номер 278
- Тип: ГДЗ, Решебник.
- Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
- Часть: без частей.
- Год: 2023-2025.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 278.
Одна сторона прямоугольника на 7 см больше другой. Какой может быть меньшая сторона, если площадь прямоугольника не превосходит 60 см2?
Ответ:Пусть меньшая сторона треугольника равна х см, тогда длина большей стороны – (х + 7) см.
Площадь равна х(х + 7) см2.
х(х + 7) ≤ 60
х2 + 7х – 60 ≤ 0
D = 72 – 4 · (–60) = 49 + 240 = 289
х1 = $$\frac{-7 + \sqrt{289}}{2 \cdot 1}$$ = –7 + 17/2 = 10/2 = 5
х2 = $$\frac{-7 - \sqrt{289}}{2 \cdot 1}$$ = –7 – 17/2 = –24/2 = –12
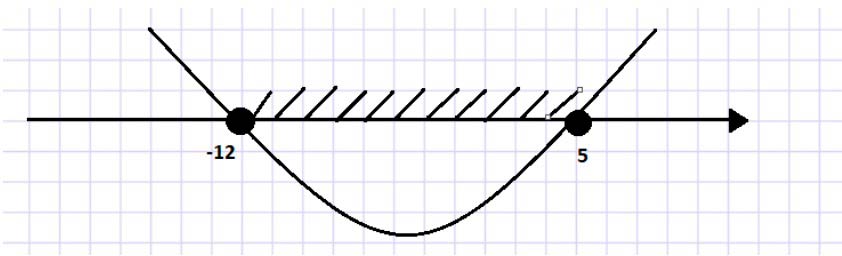
Имеем, что х ∈ [–12; 5]. Так как, х > 0, то длина меньшей стороны больше нуля, но не превосходит 5 см.
Ответ: (0; 5].
Конец страницы
Нашли ошибку на сайте? Помогите нам ее исправить!
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.