Алгебра 8 класс учебник Макарычев, Миндюк ответы – номер 983

а) $$ \left\{\begin{array} { l } { x + 6 \geq 0 } \\ { 2 x - 5 \geq 0 } \\ { \sqrt { x + 6 } - \sqrt { 2 x - 5 } \neq 0 } \end{array} \left\{\begin{array}{l} x \geq 0 \\ 2 x \geq 5 \\ \sqrt{x+6} \neq \sqrt{2 x-5} \end{array}\right.\right. $$ $$ \left\{\begin{array} { l } { x \geq 0 } \\ { x \geq 5 : 2 } \\ { x + 6 \neq 2 x - 5 } \end{array} \{ \begin{array} { l } { x \geq 0 } \\ { x \geq 2 , 5 } \\ { x - 2 x \neq - 5 - 6 } \end{array} \} \left\{\begin{array} { l } { x \geq 0 } \\ { x \geq 2 , 5 } \\ { - x \neq - 1 1 } \end{array} \left\{\begin{array}{l} x \geq 0 \\ x \geq 2,5 \\ x \neq 11 \end{array}\right.\right.\right. $$

    [2,5; 11) ᴗ (11; +∞)
б) $$ \left\{\begin{array} { l } { 2 x - 1 \geq 0 } \\ { x + 1 \geq 0 } \\ { \sqrt { 2 x - 1 } - \sqrt { x + 1 } \neq 0 } \end{array} \left\{\begin{array}{l} 2 x \geq 1 \\ x \geq-1 \\ \sqrt{2 x-1} \neq \sqrt{x+1} \end{array}\right.\right. $$ $$ \left\{\begin{array} { l } { x \geq 1 : 2 } \\ { x \geq - 1 } \\ { 2 x - 1 \neq x + 1 } \end{array} \left\{\begin{array} { l } { x \geq 0 , 5 } \\ { x \geq - 1 } \\ { 2 x - x \neq 1 + 1 } \end{array} \left\{\begin{array}{l} x \geq 0,5 \\ x \geq-1 \\ x \neq 2 \end{array}\right.\right.\right. $$

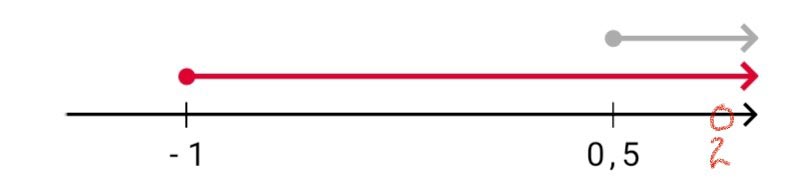
    [0,5; 2) ᴗ (2; +∞)