Алгебра 8 класс учебник Макарычев, Миндюк ответы – номер 692
- Тип: ГДЗ, Решебник.
- Авторы: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.
- Часть: без частей.
- Год: 2019-2024.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Номер 692.
.jpg "Изображение решения по алгебре 8 класс Макарычев, Миндюк, Нешков, Суворова номер 692")
Номер 692.
В системе двух уравнений с двумя переменными первым является уравнение у − |х| = 0, а вторым − уравнение вида у = kx + b, где k и b − некоторые числа. Известно, что прямая − график второго уравнения пересекает ось х в точке (−3; 0). Подберите в уравнении y = kx + b коэффициенты k и b так, чтобы система:
1) имела два решения; 2) имела одно решение; 3) не имела решений.
Ответ:Построим график функции у = kx + b и точку а.
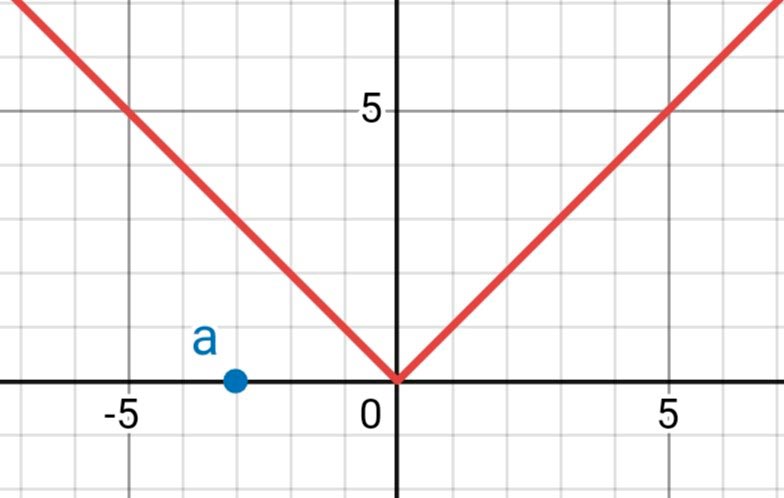
1) для того чтобы система имела два решения нужно, чтобы угловой коэффициент был положительным и меньше 1. Возьмем k = 1/3, b = 1
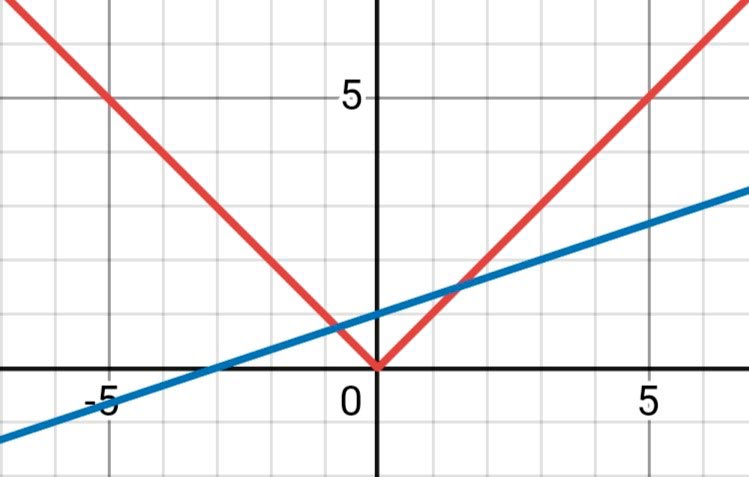
2) для того чтобы система имела одно решение нужно, чтобы угловой коэффициент был положительным и не меньше 1 или отрицательным и меньше −1. Возьмем k = 1, b = 3
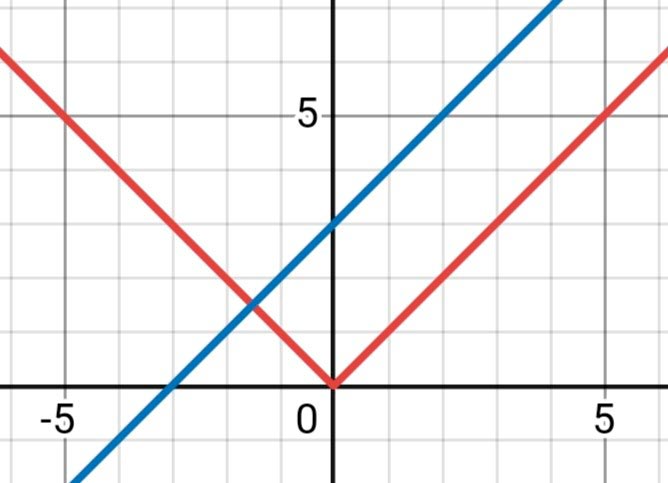
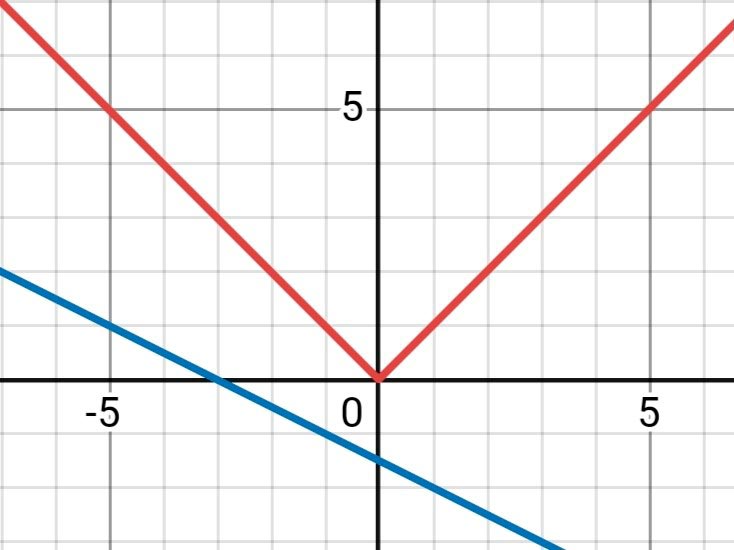
3) для того чтобы система не имела решений нужно, чтобы угловой коэффициент был отрицательным и не меньше −1. Возьмем k = −1/2, b = −3/2
С подпиской рекламы не будет
Подключите премиум подписку со скидкой в 40% за 149 ₽
Напишите свой комментарий.